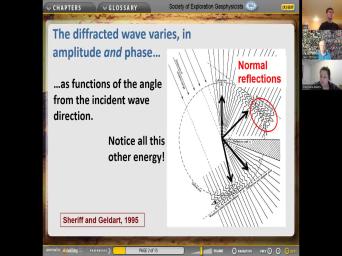
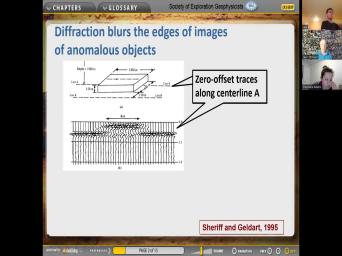
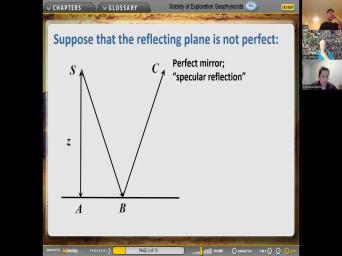
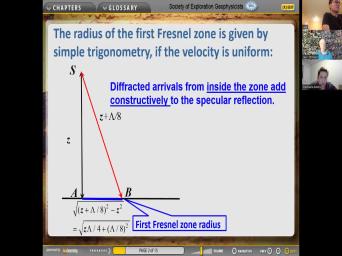
| 00:05 | So here we are on the afternoon September three resuming the the discussion about |
|
| 00:15 | reflections and refraction. So what we this morning was uh what I'll say |
|
| 00:22 | a major topic for expression. Geophysicist analyzing the amplitudes from uh subsurface reflectors |
|
| 00:34 | using the same methods uh perhaps with insight than our standard in the in |
|
| 00:42 | industry. So now I want to return to uh the same topic with |
|
| 00:51 | different aspect, which is the reflections the free surface, not from interior |
|
| 00:59 | but at the free surface. And it's normally the surface, the interface |
|
| 01:03 | reflects them because it's uh has the contrast, you know, air above |
|
| 01:12 | uh rocks or water below. So because of that, it generates a |
|
| 01:19 | of surface related multiples, which we'll about multiples in the next lecture. |
|
| 01:26 | the marine contact, it generates source and receiver ghosts. Let's make sure |
|
| 01:31 | know what those are. Uh in marine survey, the sources are towed |
|
| 01:36 | one m below the sea surface. uh the or maybe on the ocean |
|
| 01:44 | . Tell us to keep that uh . Uh and the sources are are |
|
| 01:53 | somewhat deeper, like maybe five or to 10 m in depth deeper. |
|
| 01:59 | the reason that's toad deeper is that it's towed too close to the surface |
|
| 02:04 | the bubble expands it breaks the surface loses all the pressure. And so |
|
| 02:11 | that might be a good thing. the the general consensus is it's better |
|
| 02:15 | keep it deeper. So that bubble going to expand and then actually it |
|
| 02:22 | and expands again and contracts again over over again, making a complicated source |
|
| 02:29 | time signature, but we know how deal with that in in processing so |
|
| 02:34 | can convert that to it effectively an source using process Professor. Yes. |
|
| 02:42 | we supposed to be looking at Einstein now? No, we're not. |
|
| 02:47 | thank you for that, I always that. So uh uh let me |
|
| 02:55 | again to share the screen properly. , how can you see this? |
|
| 03:09 | Yes, Okay, sorry about As we were talking, I was |
|
| 03:14 | , I think we're reading off of right now. Uh do you hear |
|
| 03:21 | ? So uh again, I did do it. Right, So first |
|
| 03:27 | me do it properly here. But I think I'm still not |
|
| 03:34 | let me back up here. Do see where it says with reflections at |
|
| 03:41 | free surface? We're still looking at . Okay, so again, I'm |
|
| 03:46 | it wrong, so forgive me. okay, now I can see reflections |
|
| 04:25 | the free surface and now we're in mode. So sorry about that. |
|
| 04:34 | of the shortcomings. Presuming like this not really as conversant as we should |
|
| 04:40 | for the technology even after two but I've got to get back so |
|
| 04:47 | hear a lot of thunder at my . Do you hear the thunder at |
|
| 04:50 | house? It's about to start and just looked at the radar. |
|
| 04:56 | So I am downtown. And if north, you'll get it in maybe |
|
| 05:02 | half an hour now. Like I , the free surface is the surface |
|
| 05:07 | reflects the most energy. And in it generates surface related multiples. We'll |
|
| 05:12 | with that in the next lecture, generates in the marine context. It |
|
| 05:18 | source ghosts and receiver ghosts. um, The source goes ghost happens |
|
| 05:26 | the uh, sources told about 5-10 below the surface bubble expands and contracts |
|
| 05:35 | expands and contracts. We have clever techniques to convert that source time signature |
|
| 05:43 | effectively impulsive signature in the data that look at. Um, but let's |
|
| 05:52 | only the first uh impulsive um The first expansion of the post That |
|
| 06:01 | energy both down and up. The that goes up, goes up five |
|
| 06:06 | and reflects off of the sea surface goes back down again. Following the |
|
| 06:11 | with a few milliseconds delay. And called the ghost. And then we |
|
| 06:17 | the same thing on the receiver The receivers are towed a bit below |
|
| 06:23 | free surface and uh upcoming wave hits receivers. And it also uh |
|
| 06:33 | as by the receivers up to the reflects back down and has received |
|
| 06:37 | So that's the receiver coast. um, those things are important because |
|
| 06:44 | reflections of the free service are so if we have our receivers on the |
|
| 06:51 | floor. The same thing is But we use different techniques to correct |
|
| 06:55 | it because of the much longer um delay in the water column. It |
|
| 07:03 | be uh significant fraction of a full uh in the water column before the |
|
| 07:10 | ways to receive. We have different for doing yeah. In the land |
|
| 07:18 | , let's consider the land, ordinary land. And we have a vertical |
|
| 07:24 | phone. Remember we have a three your phone, let's do that. |
|
| 07:29 | components your phone on a stake uh in the ground. And uh so |
|
| 07:37 | call that exactly at the surface. mind that uh instrument packages, maybe |
|
| 07:44 | inch or two above the surface that going to neglect that. But uh |
|
| 07:48 | incoming way comes up and reflects and some of its energy going back down |
|
| 07:55 | . But all the time it's doing , the instrument is recording. So |
|
| 08:03 | does not record the incoming way, records a combination of both the incoming |
|
| 08:08 | the outgoing waves altogether. They shape surface together and the instrument is recording |
|
| 08:14 | . So we need to understand how uh number one, we need to |
|
| 08:22 | uh oh Um the waves interact and two. There's gonna be an implication |
|
| 08:30 | that for how we um um interpret . So, because of this strong |
|
| 08:40 | , uh the big difference between uh the interface and above the interface at |
|
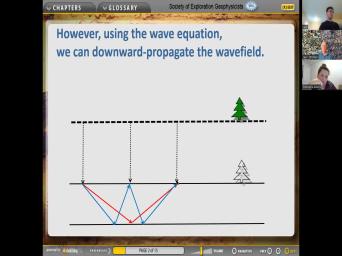
| 08:48 | free surface, we can't use the theory that we just used. So |
|
| 08:53 | got to consider the application at the surface of this complicated expression which comes |
|
| 08:59 | and richards at the free surface. we have an upcoming wave so that |
|
| 09:07 | air is uh subscript two because it's the other side of the interface. |
|
| 09:16 | we think that the incoming wave is going down and so subsequent to is |
|
| 09:22 | the lower war medium. But here up the incoming wave is coming from |
|
| 09:29 | . So the uh the air on other side of the interface is zero |
|
| 09:37 | both P. And S. And for density. Now you look at |
|
| 09:41 | formula and you can see those things in the denominator. So we can't |
|
| 09:45 | divide by zero. So instead we're to consider the limiting behavior of this |
|
| 09:53 | as these quantities here approach zero. as they approach the what we're going |
|
| 09:58 | find that it makes uh We can that issue and we never have to |
|
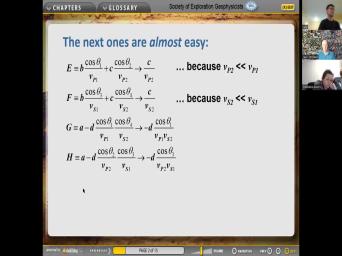
| 10:05 | the issue of dividing by zero. the first part of this program is |
|
| 10:10 | . We're gonna consider the uh we're consider the effects this into these uh |
|
| 10:21 | coffees, B, C, A D. That's what we're having. |
|
| 10:26 | here is the definition of A. so I have to do is set |
|
| 10:29 | equal to zero and set this equal zero. And we're left with only |
|
| 10:35 | other chart which is this go through other um coefficients like that and they |
|
| 10:41 | simplify substantially because uh the quantities with to oral zero. Yeah, let's |
|
| 10:52 | this. The cosine of Theta two defined as the square of the |
|
| 10:56 | one square root of one minus the squared of theta two. And the |
|
| 11:02 | of theta is equal to P X VP to uh that comes from Snell's |
|
| 11:08 | and we already know that VP So this becomes something I one and |
|
| 11:13 | same thing with the co sign for of theta four. Remember these are |
|
| 11:18 | angles on the other side of the . So these are the angles up |
|
| 11:23 | the air. Next thing we're gonna is um uh these coefficients here and |
|
| 11:30 | is the definition, I mean uppercase here is the definition of um e |
|
| 11:39 | remember what we're considering is a case VP- two is not zero but it's |
|
| 11:44 | , it's much smaller than this. since we're dividing by a small |
|
| 11:48 | we can neglect this term and keep term only. So that's this Co |
|
| 11:57 | is one that COVP- two. That's the Lebanon case because VP- two is |
|
| 12:04 | lot less than VP- one and then we're gonna let it go all the |
|
| 12:08 | to go. So the same thing these others, They simplified down because |
|
| 12:15 | these uh special case. So then quantity D, Which is this um |
|
| 12:25 | here, because here is the definition of D. And we put into |
|
| 12:32 | definition, these uh special cases that just saw, for example, |
|
| 12:38 | Is this one and f. Is one? And the product is this |
|
| 12:44 | ? And you can see that uh among these two terms. These two |
|
| 12:51 | come come from these two terms, you can see the comment in here |
|
| 12:55 | the product of one over V. . Two times V. S. |
|
| 12:59 | let's factor that out. Okay, now we're all ready to go back |
|
| 13:06 | this complicated expression and we're gonna find dominant terms in here in the case |
|
| 13:12 | we're Okay, man? Yes. , so we already decided that this |
|
| 13:21 | of this v. p. two the uh um the non denominator this |
|
| 13:29 | dominates over this one. So we're gonna set this 1 to 0. |
|
| 13:33 | way, we're gonna set this 1 0. And then putting in what |
|
| 13:40 | just found for F. And Uh was in here and then we're |
|
| 13:46 | factor out uh The Denominator v. two times v. S to put |
|
| 13:54 | right over here. And uh so you see, we have um we're |
|
| 14:03 | dividing by zero here, but that's gonna lead to infinity because of |
|
| 14:10 | Uh let's look at what we just for d. This product, what |
|
| 14:18 | uh discovered in the uh two pages , that product is not infinity, |
|
| 14:26 | it's this. And so uh putting all of that into the reflection coefficient |
|
| 14:37 | we just simplified it, we get expression and you see here nowhere here |
|
| 14:43 | we dividing by zero? We have small, slow this parameter here, |
|
| 14:50 | going to account for the um offset . And to the extent that these |
|
| 14:56 | are not one, that's also the dependence. But let's look at normal |
|
| 15:01 | and at normal incidence that this is be a zero. And so we |
|
| 15:06 | c squared, this is gonna be zero. So we get c squared |
|
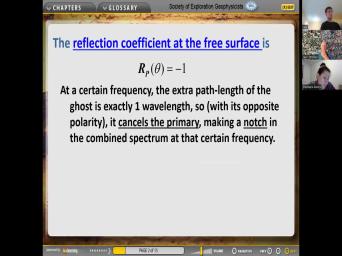
| 15:10 | notices minus one here, so that normal incidents, we get The reflection |
|
| 15:16 | is zero actually, etc, reading and I read it wrong that normal |
|
| 15:22 | , the reflection coefficient is -1. that means that a normally incident term |
|
| 15:31 | all of its energy exactly. Back . None of them gets propagated into |
|
| 15:37 | uh into the enter the air. , um that's a normal incidence. |
|
| 15:48 | about at oblique incidence? Well, we get too oblique instance, we're |
|
| 15:53 | uh the same calculation for the converted coefficient. This is the definition of |
|
| 16:01 | as we define it. Several pages . Many pages back at the free |
|
| 16:06 | , that one this one reduces to Uh this using the same approximation as |
|
| 16:16 | just did. And now let's consider special case of normal incidents. And |
|
| 16:22 | thing is a zero zero. So get uh conversion coefficient and normal |
|
| 16:31 | That's what we found before. And we still have that and so that's |
|
| 16:38 | hard zero now. Um Okay, let's uh remember that this surplus receivers |
|
| 16:49 | all these three things all together at same time, because while it's recording |
|
| 16:55 | incident way, the reflected wave has left yet and the converted share wave |
|
| 17:00 | not left. So vertically incident what is this, this some of |
|
| 17:07 | , the recording uh instruments is given this here is the sum of the |
|
| 17:13 | , uh factoring out the W0, in here, the reflection coefficient for |
|
| 17:21 | oh uh Normally incident p way uh here we just decided that's a |
|
| 17:32 | And so uh the outcome of all is that some of the waves uh |
|
| 17:39 | due. So this is what is measured by the instrument at the |
|
| 17:45 | it's the twice the incident at. that's what we meant at home. |
|
| 17:55 | that's part of what we meant when talks about the interaction of the wave |
|
| 17:58 | the free service, the free service the amplitude because it includes this reflected |
|
| 18:07 | as well as the incident, interesting that our instruments uh are located at |
|
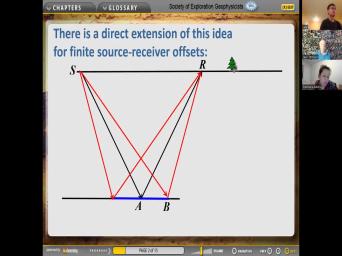
| 18:16 | point where the where the signal is insurance. Now let's consider the same |
|
| 18:27 | and that's true. Uh What we said is that's true for uh any |
|
| 18:33 | insurance, no matter what's below. service. As long as we have |
|
| 18:37 | above it, that's what we're going get for the normal it's away. |
|
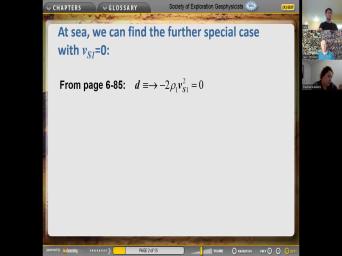
| 18:41 | let's consider the special case of the environment. And so uh in that |
|
| 18:46 | uh the incoming, the sheer the velocity and the incident medium is also |
|
| 18:55 | . So from the previous work, can decide that this uh four case |
|
| 19:03 | is zero in this special. And remembering that this is what we um |
|
| 19:10 | derived for the for the the wave , car fishing. And now let's |
|
| 19:17 | assume this quantity is zero. But we assume that D. Is |
|
| 19:23 | So uh this thing disappears. And thing disappears for all incident angles, |
|
| 19:29 | matter what is the value of piece act, no matter what is these |
|
| 19:33 | of these other things? Because of D squared out here. That goes |
|
| 19:39 | and we'll have some C squared over squared with a minus one and there |
|
| 19:42 | is. So in the marine environment get the reflection coefficient of minus one |
|
| 19:48 | all angles, all internet shopping in bleak wave coming up to the bottom |
|
| 19:55 | the sea, to the sea surface the bottom is going to reflect |
|
| 20:01 | And at the uh going back downwards the same angle first, back |
|
| 20:08 | no matter what is the incentive Now this assumption assumes a flat sea |
|
| 20:15 | . I suppose there are waves on surface of the sea. So that's |
|
| 20:21 | to what we call a rude ghost because the sea surface is not |
|
| 20:29 | That makes a complication. Which we want to go into in this |
|
| 20:35 | But I'll just remind you that uh here is that the C circuits is |
|
| 20:45 | perfect flat plane interface. Maybe not , especially in winter time when the |
|
| 20:52 | is blowing and so on, the are high. So you know, |
|
| 20:56 | the waves are only one inch, cares? But if the waves are |
|
| 20:59 | 10 ft maybe that makes a And so um that's something for you |
|
| 21:04 | keep in mind if you're looking at data taken um under weather conditions. |
|
| 21:15 | . Um See service might not be . And what happens if you're doing |
|
| 21:21 | survey and it takes several weeks and weather is changing during those weeks, |
|
| 21:26 | conditions might be different at the beginning survey. The towards the end, |
|
| 21:33 | something that you might want to keep mind. You know, we make |
|
| 21:36 | these assumptions and they are more or plausible. More or less most of |
|
| 21:42 | time. But not always. It's a good idea. Whenever you see |
|
| 21:46 | puzzlement in the data to think about did we assume didn't happen that might |
|
| 21:52 | happening in this in these data. of course similar argument is gonna show |
|
| 22:00 | converted wave is zero for so uh uh now here's a little quiz at |
|
| 22:10 | free surface on land. Uh which these answers gives uh It is |
|
| 22:24 | Uh Stephanie, I'm talking to Um Wouldn't it be d cause it |
|
| 22:31 | our PP of zero is negative That's correct. Okay, that's |
|
| 22:38 | Normal minus one. Um This is true in general and this is never |
|
| 22:48 | . So you are correct? None these good analysis. How about at |
|
| 22:54 | ? The only difference here is we're sea instead of on land. This |
|
| 23:02 | is c Yeah, okay, now is an interesting um this is an |
|
| 23:12 | public and you know, before I to this topic, I want to |
|
| 23:17 | this, stop sharing and I want um um show you those movies that |
|
| 23:34 | didn't show. It turned out that the files were fine. Only I |
|
| 23:39 | trying to open them with the wrong application. So when and I did |
|
| 23:45 | get the chance to put them in blackboard yet, I'll do that. |
|
| 23:51 | uh you can uh you can these work for you if you have the |
|
| 23:57 | application and I'm not sure what applications have for showing movies. But if |
|
| 24:02 | get an error message like we just earlier, it's because it's the |
|
| 24:07 | And so what I'm gonna do is yeah show the movie. And the |
|
| 24:24 | thing I'm gonna show is called S. P. And S |
|
| 24:29 | Well dinner all night used the wrong again. Sorry, I have to |
|
| 24:37 | it with which works. So for , I'm using something called cool file |
|
| 24:47 | and I think it's free. Uh you don't, wow, you don't |
|
| 24:55 | it. I think you can find on the internet for free. Or |
|
| 24:58 | maybe something else that you have on computer or viewing movies in mpeg |
|
| 25:05 | Um That'll also work. So let now show you this. I'm gonna |
|
| 25:15 | , I'm going to span the zoom , share my screen and I'm gonna |
|
| 25:25 | that viewer. Okay, so you see the application, what I'm going |
|
| 25:36 | launch it. Okay, can you this movie? Yes. Okay. |
|
| 25:44 | it again. Okay. And in is uh now these are showing, |
|
| 25:54 | only way I can do it is don't have a way to uh repeat |
|
| 25:58 | . So I'm gonna have to trigger and over again. So this is |
|
| 26:01 | the displacement of the way, it's a way front, it's the |
|
| 26:05 | And you can see the way of down and reflecting back up and going |
|
| 26:10 | And now look at the little red . Uh Can you see that uh |
|
| 26:19 | it goes on now it converts to can you see the shear wave going |
|
| 26:22 | in red? There you go. transmitted in red see the little circles |
|
| 26:31 | oscillating side wins as it goes You see that? Uh Yeah, |
|
| 26:39 | . Oh I know, but what want to do, I'm going to |
|
| 26:43 | that. Okay now it's uh on screen. Oh okay so here we |
|
| 26:54 | . See the shear wave uh converted moving slower. Okay so I will |
|
| 27:08 | this to uh the black warm and can do this for yourself and I'm |
|
| 27:15 | stop sharing this and minimize this The other movie this way, Front |
|
| 27:36 | , this one's more interesting. I'm share my screen, expand the |
|
| 28:02 | you can see the movie already to . Oh Watch This one. So |
|
| 28:10 | is uh a wave coming down from upper left. You see it's coming |
|
| 28:17 | from the upper left and the bright moving to the lower right, that's |
|
| 28:22 | incident way and it's curved. It's like the plane waves that we have |
|
| 28:28 | , it's definitely curved. So now can see uh let's contract on the |
|
| 28:36 | on the transmitted wave so frustrating the mr wave and you can see that |
|
| 28:42 | has a little kink at the Uh But it's um um uh Not |
|
| 28:52 | at all at all, I would . Yeah I just learned how to |
|
| 28:57 | it. Uh I'm gonna advance it little bit more or so, you |
|
| 29:03 | see the pink here. And so this up here is a circle whose |
|
| 29:09 | is over here and this uh this is a circle whose origin is um |
|
| 29:18 | in here somewhere and you can see radius of curvature. This is a |
|
| 29:21 | bit different than the radius of curvature because the velocity is different down |
|
| 29:25 | but the apparent velocity is the same both modes. You've got to have |
|
| 29:30 | two wave fronts, the uh this and this one they've got to travel |
|
| 29:37 | horizontally along the, horizontally along. . Now let's look at the reflected |
|
| 29:50 | . So here is the reflected wave and I know you're accustomed to think |
|
| 29:55 | a reflective array which is going up this record. This is a reflected |
|
| 30:00 | front, so maybe a little bit in front, but you can see |
|
| 30:05 | it's a circle with the same radius curvature as this one and the center |
|
| 30:11 | that circle is down here. This what we call the mirror point |
|
| 30:15 | So this apparent source down here, the center of this circle down here |
|
| 30:22 | is uh the mirror image of the source, which is over here |
|
| 30:28 | And so uh this wavefront has a and a trough and a peak in |
|
| 30:33 | conflict. So now this part here the converted share waves, how do |
|
| 30:38 | know that? It's because of moving , you see uh this one is |
|
| 30:43 | ahead and so this is a convert right now. And uh do you |
|
| 30:48 | a converted way of going down? don't see one. Uh let's uh |
|
| 30:56 | the uh I do not see a way uh, in transmission. |
|
| 31:14 | uh, whoever made this calculation, think did not include that. So |
|
| 31:20 | a special case of the lower which doesn't have um, converted transmitted |
|
| 31:30 | special place. Okay, so, , I encourage you all to play |
|
| 31:36 | this on your own tonight and during the week and uh, stay |
|
| 31:46 | it until, until nothing more is . I'm gonna share the screen. |
|
| 31:55 | . Um, what's your, and we're gonna talk about critical angles. |
|
| 32:05 | so, um, first thing I you're thinking is that we don't have |
|
| 32:16 | angles in our data. Well, that's true and maybe not. |
|
| 32:22 | uh, in our data, we we normally know what depth range we're |
|
| 32:27 | for. So we're looking for a , that's about two kilometers long, |
|
| 32:35 | km deep, something like that, three km deep. And so we |
|
| 32:41 | out um, receivers. So that links, I have a corresponding maximum |
|
| 32:49 | when, when I was young, I was your age, it was |
|
| 32:55 | decided to have a maximum offset to approximately equal to the depth to the |
|
| 33:05 | . So that means uh, 2 km alone. So about the |
|
| 33:14 | I came into this industry, we a V. O. And so |
|
| 33:19 | if we want to have um, want to study the, the offset |
|
| 33:25 | of amplitudes. The popular thing to is have, um longer offsets. |
|
| 33:33 | we've got to have longer and longer . And so these days we have |
|
| 33:39 | as much as 10 kilometers long for a three kilometer depth right now. |
|
| 33:48 | it's true for the for the horizon interest. We never we never include |
|
| 34:03 | which are imply after we've done our all converted offset angles. We don't |
|
| 34:09 | to have any angles in our Any incident angles in our dataset, |
|
| 34:16 | at the receiver. Uh no incident the interfaces. We don't want to |
|
| 34:22 | any incident angles in our data which uh post critical or even near the |
|
| 34:29 | because we know that if if we those kinds of angles, weird things |
|
| 34:36 | now consider this. Maybe we could smarter and we could learn something from |
|
| 34:43 | near critical post critical angles. That's good topic for a graduate student is |
|
| 34:51 | consider what we might learn from the which is intentionally excluded from our from |
|
| 35:01 | consideration. Like I said, normally we limit the length of the off |
|
| 35:08 | . I uh just don't those receivers in out of the field, save |
|
| 35:16 | by not uh installing receivers that we want to use the data from. |
|
| 35:23 | , there are, there are lots cases where that is improved. For |
|
| 35:31 | , suppose we're doing an ocean bottom , uh maybe as far as we're |
|
| 35:38 | a land service and so we put a bunch of geophones in a |
|
| 35:43 | We're gonna do three D. In uh in this year, of course |
|
| 35:47 | gonna do three D. You can of to day if you want and |
|
| 35:51 | put out our receivers and then uh for that we don't and I put |
|
| 35:59 | out online uh on stakes in the . And then we start vibrating. |
|
| 36:07 | don't vibrate in the middle of this . We don't we don't start our |
|
| 36:12 | in the middle of the array. don't start our vibrations uh at the |
|
| 36:18 | of the array. No, we our vibrations outboard of the array. |
|
| 36:22 | this is to get what we call proper migration aperture. So we start |
|
| 36:30 | so maybe we'll start our vibrators, two or three kilometers outside the |
|
| 36:37 | And then we work towards the right and forth lines of uh uh horses |
|
| 36:45 | so on and according to all those . And then while we're and then |
|
| 36:51 | we're doing it we passed through the the array. And pretty soon we're |
|
| 36:56 | in the middle of the array. then we pass out the other side |
|
| 37:01 | we're vibrating from the from the other . But everything to do is while |
|
| 37:05 | vibrating, say we're vibrating to the of the array. Our vibrating and |
|
| 37:12 | closer to the array with every shot . We've got our crew working and |
|
| 37:18 | installing more receivers in the ground on east side of the race. So |
|
| 37:25 | start off to the west and we're our way east and as we're working |
|
| 37:29 | way east, the crew is installing and more vibrators to the east. |
|
| 37:33 | then as we get in the middle the array and proceed through, we |
|
| 37:38 | to pick up those uh, those most receivers and uh move them around |
|
| 37:47 | install them again ahead of the shock . So we call that rolling the |
|
| 37:54 | and this is very common. We a finite number of receivers and so |
|
| 37:59 | gonna put as many as we can the ground and then we're putting more |
|
| 38:03 | the ground to keep ahead of the . So think about that. |
|
| 38:09 | I say we start three km west the array and suppose the array is |
|
| 38:17 | km wide set, supposed to eastern is uh three km east of the |
|
| 38:27 | , Western of the Western. Now , so that means that as we |
|
| 38:32 | vibrating, we have um offsets of kilometers three kilometers of of no receivers |
|
| 38:43 | then three kilometers and receivers and we're more 3.13 point two etcetera. And |
|
| 38:49 | we, as we are working. so we have in our data set |
|
| 38:54 | long offsets in this case six kilometer . And in many cases we can |
|
| 39:01 | 2030 kilometer offsets in our data. , because of the way we operate |
|
| 39:09 | the field, answer nationally. The thing we do is we had to |
|
| 39:14 | away those far far Austin's, but we don't throw them away. Sometimes |
|
| 39:21 | keep them in the computer and we don't look at them. So that's |
|
| 39:27 | crime that, that's a crime that be uh punishable by death because we've |
|
| 39:34 | good money to acquire those. And it's, it's a real shame if |
|
| 39:40 | not a crime, it's a real to not even look at them. |
|
| 39:43 | the reason, of course we, , look at them is we have |
|
| 39:48 | in our thinking and embedded in our and, you know, our analysis |
|
| 39:52 | everything. The idea that we have and moderate offsets maybe for our |
|
| 39:58 | but not really, not really very . So we don't have normally most |
|
| 40:04 | incident angles at the target horizon in analysis. So if we have them |
|
| 40:11 | our data, let's just uh, in the archives somewhere don't even bother |
|
| 40:19 | at them. Well, so that's real opportunity for a university like |
|
| 40:23 | Uh, we can talk, we talk to these oil companies who do |
|
| 40:28 | and say give us this very long data. We'll have some smart students |
|
| 40:34 | at it and maybe they'll come up something interesting will cost you much. |
|
| 40:40 | should give us access to the maybe give us a few bucks to |
|
| 40:44 | for the graduate student scholarship and so . It's gonna be a lot cheaper |
|
| 40:50 | having your expensive people at, who they might have came up with something |
|
| 40:57 | , maybe not, but you there's nothing good is gonna come of |
|
| 41:01 | data while it's sitting in, your gathering dust. But maybe we could |
|
| 41:07 | something good at the University of Houston you just give us access to the |
|
| 41:12 | . So as a matter of last week I made that exactly that |
|
| 41:16 | to a hess and they seem to receptive and so maybe we'll get some |
|
| 41:23 | from hess in the near future uh the sort that uh, they don't |
|
| 41:28 | to look at themselves, but they it in their archives and uh I |
|
| 41:35 | you'll share it with us. Now have a question about the long |
|
| 41:42 | So how do you define the survey , which has a long spring? |
|
| 41:52 | , depend on velocity of the frequent of the data you want, |
|
| 41:58 | it depends upon the national offset and depths of the reflection. So you |
|
| 42:04 | imagine that say you have a maximum in your data of say three |
|
| 42:11 | So uh the reason you have that of 17 kilometers is because you didn't |
|
| 42:17 | all those extra G. F you didn't pay the crew to put |
|
| 42:22 | in the ground because you know that maximum offsets you want to look at |
|
| 42:29 | to incident angles at the reflector of like 40 45 degrees maybe anymore, |
|
| 42:36 | last week. You know that you not want to look at these critical |
|
| 42:42 | . And so you don't have um far far offsets uh acquired in the |
|
| 42:48 | because that's expensive and you don't want do it if it's gonna cost you |
|
| 42:52 | . But now just so we have maximum offset three km and uh say |
|
| 43:01 | maximum all set up of six killer , depth to the reflector of three |
|
| 43:07 | . And so we figured that's gonna us angles, maximum angles around 40 |
|
| 43:13 | 50 degrees. And we think that's pretty critical if if it turns out |
|
| 43:19 | some critical angles uh included in those . That data, we might just |
|
| 43:26 | that because of the peculiar amplitude which we're gonna talk about charlotte and |
|
| 43:32 | probably just mute those out. So don't look at those at all. |
|
| 43:36 | now, in the same situation, maximum set six km. You |
|
| 43:45 | there's gonna be other reflectors shallower in subsurface, say, instead of three |
|
| 43:51 | depth in the subsurface, say it's one kilometer depth in that case, |
|
| 43:58 | our far offsets, we're gonna have wide angles of incidence, probably post |
|
| 44:07 | . So we already have those in data at shallow offsets because we've designed |
|
| 44:15 | acquisition geometry for the target depths, at all shallower depths we're gonna have |
|
| 44:22 | their offsets which are gonna probably be most critical and certainly going to be |
|
| 44:28 | non hyperbolic move out. And so smart thing to do, everybody thinks |
|
| 44:34 | smart thing to do is to just far off sets out. No, |
|
| 44:40 | anymore with the same argument maybe. there's some really interesting information in there |
|
| 44:48 | the subsurface of shallow that we're not ourselves to think about because we we |
|
| 44:55 | use those data. So let's uh we aren't gonna learn anything from those |
|
| 45:04 | far offsets, uh let's look at following analysis for post critical incidents. |
|
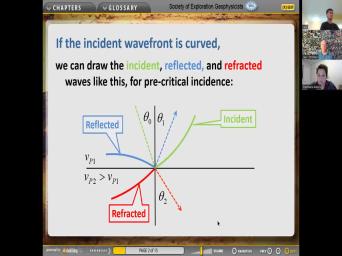
| 45:14 | gonna put myself into presentation mode and what we said about Snell's law. |
|
| 45:23 | the transmitted p way, the sign the, of the angle is equal |
|
| 45:28 | sine of the incident angle times this ratio where this is the incident |
|
| 45:33 | that's reflecting then for uh the case the lower medium is faster then for |
|
| 45:41 | large angles sign of 32 is going be greater than one. So this |
|
| 45:48 | , this is a real number. of theta one. Sine of theTA |
|
| 45:51 | is always going to be less than 45 degrees. But uh under uh |
|
| 45:58 | conditions, if the velocity ratio here enough, then we're gonna have sine |
|
| 46:04 | theTA two can be greater than one the point, the offset where it |
|
| 46:10 | begins to get weird is where X equal to one. And so we |
|
| 46:15 | that incident angle the critical angle that's by this philosophy ratio, which is |
|
| 46:21 | than one by assumption. This ratio greater than one under these circumstances. |
|
| 46:27 | is the inverse of that. This um ratio is less than one, |
|
| 46:32 | it should be for uh this angle is always a real angle and we |
|
| 46:39 | have Snell's law. And every quantity you see here is real. That's |
|
| 46:44 | , that's real, That's real. is real. But the co sign |
|
| 46:50 | not necessarily real under these circumstances. because it can happen that this thing |
|
| 46:56 | it's real, it's bigger than So when the square uh or maybe |
|
| 47:02 | bigger than -1, if that's a number, this is a negative number |
|
| 47:06 | the square of it's gonna be a number greater than one. So uh |
|
| 47:10 | co sine of this angle is gonna imaginary. This is bigger than one |
|
| 47:17 | sine dominates and we'll have a minus under the square root sign. So |
|
| 47:25 | gonna give an imaginary memory. So though this thing is real, if |
|
| 47:31 | bigger than one, the cosine of act is imaginary because it was there |
|
| 47:39 | critical reflectivity is complex. And so the same formula that we looked at |
|
| 47:47 | . So let's first consider the implications this for the post critical transmitted p |
|
| 47:55 | vector. So that's we call that two and as magnitude omega or a |
|
| 48:02 | . And uh this gives the two . And uh so putting in here |
|
| 48:09 | the Kassian is one minus the sine . And taking out the square root |
|
| 48:13 | minus one. Then here's the eye here. So this is now sine |
|
| 48:18 | minus one under the radicals. One these circumstances that positive number positive. |
|
| 48:28 | that's a real number right here. see an explicit I now let's put |
|
| 48:36 | understanding of the wave vector into this for the wave and here's K dot |
|
| 48:44 | . And so uh the kid dot has been multiply this quantity uh times |
|
| 48:54 | uh theater this X factor. It has magnitude offset X in the X |
|
| 49:12 | here, that's one. And so wow, what you see in the |
|
| 49:20 | bracken's is the dot product between K and X. And let's um you |
|
| 49:32 | have the minus. Uh still have eye out here. That's this |
|
| 49:36 | I have the mega T here, this mega T. And so now |
|
| 49:41 | separate out this part here uh that's what we have down here and |
|
| 49:46 | have this i times this. I some minus one and no more eyes |
|
| 49:52 | . Here's an eye. This thing going to oscillate. But this thing |
|
| 49:56 | gonna decrease with increasing death because of minus. Uh because we already decided |
|
| 50:15 | the cosine of theta two transmitted data imaginary. That's gonna make the amplitude |
|
| 50:22 | . So the transmitted wife is phase from that of the incident way the |
|
| 50:31 | is true of post critical reflected and a way of afternoon. But let's |
|
| 50:35 | on this transmitter as it travels along boundary beneath the interface with this apparent |
|
| 50:46 | . The transmitted P way forces the mediums oscillated at the same apparent |
|
| 50:51 | That's uh this is the same. is Snell's law insists that these apparent |
|
| 50:58 | . This one further lower media. one from the incident has to be |
|
| 51:02 | same. And that's gonna be a of which is bigger than V. |
|
| 51:07 | . One. Because we already decided uh Sine of theta one. Of |
|
| 51:14 | , that's uh um that is less one. This is a real uh |
|
| 51:22 | number. This one is also a number, but it's bigger than |
|
| 51:27 | this is less than one. uh current velocity is greater than the |
|
| 51:33 | philosophy. What happens then? What that do? This forces? This |
|
| 51:40 | a new way a plane wave radiates into the incident meeting. Now, |
|
| 51:45 | is this way? If the incident is plainer? This is just a |
|
| 51:50 | critical reflected P wave propagating up at angle incident angle. We already did |
|
| 51:58 | . But if the incident wave is , this is a new wave propagating |
|
| 52:04 | at the critical angle. So, gonna show you a diagram of that |
|
| 52:09 | . Just point out here that it happen that uh if you have a |
|
| 52:15 | fast medium down below, then the wave velocity down below is bigger than |
|
| 52:20 | p wave velocity up above. Maybe assault? Uh assault. But in |
|
| 52:25 | case there's a sheer critical angle uh um it's always gonna be a bigger |
|
| 52:31 | angle. That's a sign data for be the most critical awesome. So |
|
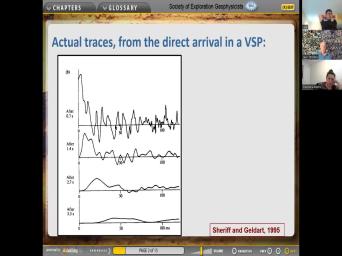
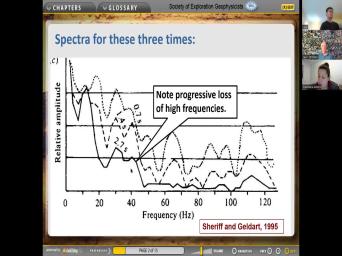
| 52:38 | can see here this is a calculation Sheriff and guild are of all the |
|
| 52:44 | behavior that can happen post critical. this complication is easy. This part |
|
| 52:53 | easy. This is transmitted here is reflected P way pre critical. So |
|
| 52:59 | the one we normally are looking at is the uh Mhm. Heard away |
|
| 53:08 | um laura Daniels, All kinds of behavior. Uh and uh that's all |
|
| 53:20 | for the model that they used That's all happening about 30° normally for |
|
| 53:25 | kinds of rocks. The critical angle happens further, it's uh they're here |
|
| 53:32 | most of the data that we look is. So before we get into |
|
| 53:39 | pictures of that most critical stuff, uh take your quiz. So uh |
|
| 53:49 | a statement and uh it's gonna be completed with all these things. Um |
|
| 53:56 | no in here we have uh all the above. So that's a possible |
|
| 54:02 | . And then there's another um uh here. And then again all of |
|
| 54:07 | above down here including this. So go through this from the top. |
|
| 54:19 | So Stephanie uh is this first one . No it I think I heard |
|
| 54:29 | say no. And so if that's then um we can't have all of |
|
| 54:35 | above here. So if this one false. Um We we better not |
|
| 54:44 | uh just we better not find more one of these answers is through. |
|
| 54:50 | let's keep this in mind. Go to number two, says number |
|
| 54:54 | the transmitted wave decreases in amplitude away the air face. Is that one |
|
| 54:59 | falls? That is true. that one is true and I'm gonna |
|
| 55:11 | back here. So now uh so we talked about that because this is |
|
| 55:23 | this is all positive and there's no hear anymore because this I got multiplied |
|
| 55:29 | this. I gave her -1. um wow sure. Uh this one |
|
| 55:47 | away as he increases the same Uh goes to zero. Eventually Z |
|
| 55:55 | big enough. Now let's look at rest of this. This shows an |
|
| 55:59 | solitary factor iomega of X. And that looks like a wave which is |
|
| 56:06 | in the X. Direction. It's propagating, it's not propagating down and |
|
| 56:14 | from the boundary. Like uh uh an ordinary transmitter way. This thing |
|
| 56:20 | trans is uh propagating parallel to the and away from the boundary. It's |
|
| 56:27 | an apple too. So now I to go back to the quiz and |
|
| 56:34 | you to reconsider your answer for a it would be parallel. Yeah because |
|
| 56:50 | only propagating in acts. It's not and Z at all. Oh I |
|
| 56:55 | . Okay okay now let's go. now we got to that part of |
|
| 57:00 | truth. So uh uh we expect find now probably either this answer is |
|
| 57:09 | or this answer is true. Let's our way down. Um uh point |
|
| 57:14 | the transmitted wave that has a shape from the incident wave. It's your |
|
| 57:24 | . Yeah, that's true because the coefficient is uh complex. And so |
|
| 57:32 | that multiplies times the way, what gonna make that it's gonna change the |
|
| 57:37 | of the wave. Good. So far we have all of the above |
|
| 57:40 | we're not done yet. So uh says here, the next one is |
|
| 57:46 | reflected wave as a shape different from incident. We didn't actually analyzed |
|
| 57:53 | We we didn't have to analyze. we didn't actually analyze the reflected wave |
|
| 58:06 | all. So this is a difficult here. Yeah. Um um here's |
|
| 58:16 | you might think in this case uh a member of the formula that we |
|
| 58:26 | for the reflected wave preferences. A formula that we got from uh and |
|
| 58:33 | . It has in there a bunch terms like co sign data to and |
|
| 58:39 | sign uh uh force. I'm I'm hearing an echo from uh from |
|
| 58:54 | here. I'm sorry I didn't I needed. So in that complicated expression |
|
| 59:05 | you can look back through your notes see that complicated expression. There are |
|
| 59:09 | numbers, there are some quantities for reflected wave which depend upon those other |
|
| 59:15 | , even though the reflected wave is uh not propagating at those ankles. |
|
| 59:23 | do see in their chosen data to cosign theta for etcetera. And so |
|
| 59:28 | things are gonna be um um complex imaginary uh in this context, post |
|
| 59:37 | . And so um I think uh that means is that the reflection |
|
| 59:47 | the p waves is gonna be complex though it didn't penetrate into the long |
|
| 59:54 | at all. And so it's also have, I'm gonna go with all |
|
| 59:59 | the above this. All of the F um includes everything. But so |
|
| 60:08 | uh if you were seeing this on on a uh final examination, you'd |
|
| 60:15 | to think about this for quite a . That's a question. If the |
|
| 60:24 | grave is a P wave in the critically reflected P wave propagates upwards at |
|
| 60:30 | critical angle, Not at the Is that true or false? |
|
| 60:36 | that one is false because we decided that it's gonna be propagating upwards at |
|
| 60:43 | incident angle whether it's pre critical or critical. And we didn't assume anything |
|
| 60:50 | there about where they were most credit . Oh okay. So uh now |
|
| 61:00 | think about both curb ways and curb . So one more of these plane |
|
| 61:11 | and no more of these plan Now we're getting real. So the |
|
| 61:18 | where a friend is curved, the critical reflection coefficient is modified by a |
|
| 61:25 | which I haven't showed you but it's to be modified by a term which |
|
| 61:29 | proportional to this. And so this the wave uh the attitude of the |
|
| 61:35 | factor times the greatest of curvature, that? That uh concept of greatest |
|
| 61:43 | curvature. Uh So if the if have a source at the surface radiating |
|
| 61:50 | into a uniform hypertrophic media, it's be uh a spherical away from |
|
| 61:58 | and it's gonna have a curvature which going to be decreasing as it goes |
|
| 62:05 | because uh it's a tight sphere at beginning and then it gets uh bigger |
|
| 62:10 | bigger sphere. And so we called radius of curvature under that simple uh |
|
| 62:17 | is the distance back to the That's the radius of the expanding |
|
| 62:25 | Now, in the real earth is gonna be a sphere anymore because you |
|
| 62:29 | layers and refraction and all that but it'll be approximately equal to the |
|
| 62:35 | back to the source along the And so that's what we mean by |
|
| 62:40 | greatest encourager. And so you can through this algebra and you can see |
|
| 62:46 | in the end we we convert this wave vector amplitude to two pi divided |
|
| 62:57 | the wavelength, it's a two pi approximately equal to six. And so |
|
| 63:03 | this ratio is uh 1/6 Approximately 1/6 the of the wavelength divided by the |
|
| 63:15 | back to the origin back to the . So that after a propagation of |
|
| 63:20 | or two wavelengths is as soon as thing gets to be one or two |
|
| 63:25 | the wavelength this correction which is implied uh is negligible. And and that's |
|
| 63:33 | valid argument ex uh for it's a argument for what happens um uh to |
|
| 63:41 | expanding wave um pretty critical that near critical angle it's gonna be different. |
|
| 63:48 | here is a picture which is kind similar, isn't it, to the |
|
| 63:56 | movie that we just saw uh and me walk our way through this. |
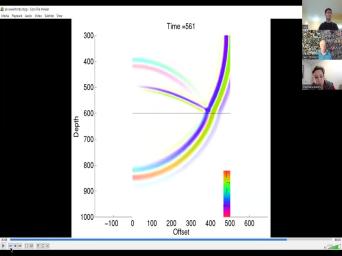
|
| 64:03 | This is the incident wave front and one also in green is the incident |
|
| 64:10 | . So you can see that this front is perpendicular to the ray here |
|
| 64:16 | then it goes a circular away And you can tell from the radius |
|
| 64:21 | curvature here that the the origin of was somewhere around in here. |
|
| 64:29 | so that's the incident way, the way is this one? And it |
|
| 64:34 | a little kink right here because this is greater than this philosophy. That's |
|
| 64:39 | it makes a kink like this not kink in the other direction, but |
|
| 64:44 | like this. So this angle is angle than this one and the ray |
|
| 64:52 | ray vector for the refracted rays. this one? Now the reflected |
|
| 64:59 | here's the reflected uh wave vector equal opposite angles expect and has a corresponding |
|
| 65:09 | that looks like. So okay, that uh that will be familiar to |
|
| 65:15 | from the uh the movie. Now this case we don't show all the |
|
| 65:21 | ways. So uh so this in there's gonna be share ways but these |
|
| 65:27 | are complicated enough without share waves. we left the share waves out. |
|
| 65:34 | these this point of intersection right here along the uh interface with an apparent |
|
| 65:42 | given here, V one over sine one has got to be exactly equal |
|
| 65:47 | B two over sign sign 32. this one gets ahead or behind the |
|
| 65:56 | um Yeah. Uh Yes, way. Now that's all pretty |
|
| 66:05 | However, now if the incident angle post critical then something new happens. |
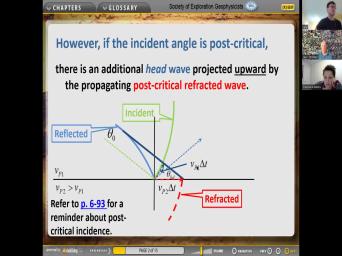
|
| 66:14 | it's post critical, then the uh . We have the velocity below is |
|
| 66:23 | than the velocity above. So this propagating horizontally, is gonna get ahead |
|
| 66:29 | anything that's happening here, but this velocity has to be the same, |
|
| 66:37 | it can be the same because this got ahead. So what that means |
|
| 66:42 | uh we're gonna have an additional This one right here. This is |
|
| 66:49 | we call a headway. We didn't that in the plane wave problem and |
|
| 66:55 | didn't see it in post critical. post here's pre critical and so post |
|
| 67:00 | . Uh that means that uh this the same incident, we can see |
|
| 67:08 | this uh incident wave is coming. Here's the here's the rate the incident |
|
| 67:14 | . Can you see this one is in at a greater angle than this |
|
| 67:19 | . So this one is coming in critical and it's incident wave front looks |
|
| 67:28 | this. So the fans middle wave down here and it's dash here because |
|
| 67:35 | didn't remember, we said that the is going away as you go |
|
| 67:41 | So this uh this is uh this is less than this amplitude. This |
|
| 67:49 | is even less. So the way was propagating in this direct parallel to |
|
| 67:56 | the interface and this apparent velocity is to the apparent velocity mm. So |
|
| 68:37 | , because the new wave which we see before, we didn't see it |
|
| 68:40 | critical and we didn't see it with waves. This happens because only because |
|
| 68:47 | waves are curved. Now, what the angle that happens here? So |
|
| 68:53 | this wave has obviously propagated upwards from uh in this direction with the P1 |
|
| 69:02 | uh in a interval delta T. meanwhile the wave down here is propagated |
|
| 69:11 | in the lower media at the P two times the same time. |
|
| 69:18 | that means the angle of this triangle here. Anyway, angle is equal |
|
| 69:25 | uh sign of these two distances. deputy that's here, VP two, |
|
| 69:34 | T. is here and the right right in here. And so uh |
|
| 69:42 | angle is the angle whose sine is by this these delta T. Is |
|
| 69:47 | app. And now you see what's is V. P. One over |
|
| 69:51 | . Two. So that means that head wave angle is critical lying and |
|
| 69:59 | a plane uh it's a straight So of course you can imagine that |
|
| 70:07 | this is in three dimensions it will the point of a cone. So |
|
| 70:14 | imagine uh cone whose point is here uh intersects the figure right here. |
|
| 70:22 | it's uh on the behind the And in front of the screen it's |
|
| 70:27 | comical surface. And now there might other head waves associated with other outgoing |
|
| 70:38 | corresponding to other critical angles. So have a really nifty figure from sheriff |
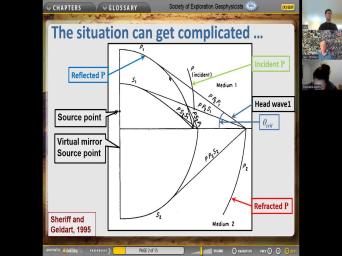
|
| 70:45 | jail dark. And let's step our through this and you will see how |
|
| 70:50 | it can be. So uh first is the incident p wave wave front |
|
| 70:58 | here and you can see that it's circle whose whose origin is here. |
|
| 71:05 | now here is the reflected P wave its origin is uh um down here |
|
| 71:17 | that that we call that the virtual point or the mirror source point. |
|
| 71:24 | Real source point is here and this is the virtual source point or this |
|
| 71:30 | reflected p wear And here is the p way uh in this case where |
|
| 71:38 | lower medium is faster than the upper . So this one got way ahead |
|
| 71:43 | this um uh convergence here. So going to step forward one at a |
|
| 71:50 | and see what I was going So this is the head wave that |
|
| 71:54 | just talked about. Uh This is angle here. And this head wave |
|
| 72:01 | this point here, where the P in the lower media got this |
|
| 72:08 | it's way ahead of these because this is faster and there's a straight line |
|
| 72:13 | goes up here and I get to tangent up here. So now here |
|
| 72:22 | the reflected few wave also coming from uh mirror point. Yeah. |
|
| 72:39 | And now there's two more headways coming in here. Uh just number them |
|
| 72:45 | and three connecting uh different points down with Yeah, reflected your way. |
|
| 72:57 | of them uh connects all the way to here and one of them connects |
|
| 73:02 | to here. Here's 1/4 head wave goes from the uh transmitted p way |
|
| 73:11 | to the reflected s way here is refracted as appears to transmit it? |
|
| 73:16 | way. And here is head wave Headway five In here, this one |
|
| 73:27 | , and the sure way of critical is given in here and here's head |
|
| 73:33 | six from here back to here. can see how uh startlingly complicated this |
|
| 73:41 | and this example is a good one it shows uh the medium below is |
|
| 73:47 | lot faster than the medium above. all these things separate. You can |
|
| 73:51 | that if this thing is if this at this point is close to this |
|
| 73:58 | , then all this stuff gets on of each other. Now these head |
|
| 74:07 | are seeing wherever the incident angles are and there's a strong velocity increase, |
|
| 74:12 | example, um where we see a between sediment and salt, or maybe |
|
| 74:20 | sediment and carbonates, um plastic sediments carbonates, and maybe between sediments and |
|
| 74:27 | . If you have long enough offsets enough angles, you're going to see |
|
| 74:32 | . And like I say, it's . So maybe it's a good |
|
| 74:36 | we ignore it, but who Maybe we could learn something if we |
|
| 74:40 | at now. We also see it the time. So these are special |
|
| 74:48 | , but here we see it all time in uh more hard logging. |
|
| 74:54 | in fact, that's the basis for borehole logging. So uh you see |
|
| 74:59 | uh you know what? This is good spot to stop and take a |
|
| 75:09 | break because um been going on for hour and quarter, let's stop at |
|
| 75:16 | point. Uh pick up again at o'clock even and we'll go into the |
|
| 75:25 | Context wave propagation now in the So I'm gonna go back here and |
|
| 75:32 | here. So in 15 minutes I'm to uh Come back and in the |
|
| 75:39 | I'm gonna stop my video and uh myself and I'll see you all at |
|
| 75:49 | . Okay, so now let's talk sonic logging groups. This um isn't |
|
| 75:57 | . I'm gonna have to stop sharing uh now I'm going to start sharing |
|
| 76:20 | . No, I can't do I'm gonna do this, start sharing |
|
| 76:31 | . This works. Okay. Can see the cartoon or the borehole? |
|
| 76:53 | . Okay. So uh now so this is a cartoon um showing what |
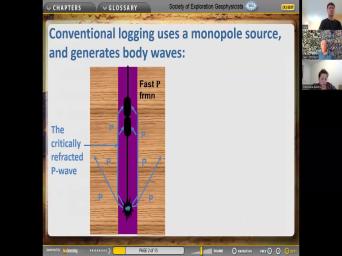
|
| 77:02 | in a conventional sonic long. So we have the formation and this way |
|
| 77:07 | up of course, and we have bar a hole here in purple. |
|
| 77:10 | we have a tool down here. and the tool has two parts got |
|
| 77:14 | source and two receivers. And so source fires in all directions. That |
|
| 77:20 | p waves through the mud. Purple at all angles. And because the |
|
| 77:30 | is faster than the mud, these refract upwards like some and the one |
|
| 77:37 | comes over here refract downwards of But uh this one refracts upwards. |
|
| 77:42 | uh for this takeoff angle here, is the critical angle where it's critically |
|
| 77:48 | along the p wave uh along the wall. And this is in cylindrical |
|
| 77:56 | . Of course, this is a section. So that that's a difference |
|
| 78:00 | what I just showed you with the wave. But aside from that geometrical |
|
| 78:05 | , it's exactly the same as we before. So as this thing propagates |
|
| 78:11 | along the boundary, it ripples the boundary like this. and it puts |
|
| 78:17 | p waves back into the mud at mud velocity, of course, all |
|
| 78:23 | here. And so when it gets to here, it's gonna emit this |
|
| 78:28 | coming up this way. And the of of of this angle is the |
|
| 78:33 | as this angle, which is the angle. And so uh when it |
|
| 78:39 | to hear it emits critic at the angle back here and this one happens |
|
| 78:42 | get this receiver and then it goes a little bit further and when it |
|
| 78:47 | to hear it, um it's this . So you can see that these |
|
| 78:52 | are receiving signals which measure the velocity the formation. And a modern tool |
|
| 79:02 | have maybe a dozen receivers instead of two, but you get the |
|
| 79:07 | So um now let's think about shear . So, so here is the |
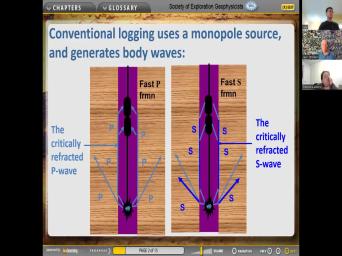
|
| 79:15 | situation in the same formation, and also want to record shear waves. |
|
| 79:22 | so the same tool will do So, here's our source down |
|
| 79:26 | And uh in addition to this wave , there is a refracted S waves |
|
| 79:31 | reflects out into the formation never comes . And this angle is uh closer |
|
| 79:38 | the um uh to the normal uh this one. So, the um |
|
| 79:50 | one is refracting away from the Hold not as much for the wave |
|
| 79:57 | travels through the mud at this You see this angle is a bigger |
|
| 80:01 | than this angle over here. So is the sheer way of critical angle |
|
| 80:08 | this point. Uh Refracted share This refracted shear wave. This one |
|
| 80:15 | propagating um exactly along the boundary. it's like this one except that it's |
|
| 80:22 | and it's propagating at the sheer velocity the mud and it's putting back sheer |
|
| 80:29 | in the formation and it's putting back the mud api way at this same |
|
| 80:35 | way of critical angle that. so then this shear wave, so |
|
| 80:40 | difference in arrival times between here and uh gives the shear wave velocity between |
|
| 80:46 | and here. You know. Also can measure the time delay between the |
|
| 80:53 | and the first receiver and that will you an average velocity in here that |
|
| 80:58 | lower resolution. Normally we don't look that. So this is the same |
|
| 81:03 | . This is the same tool as have here. And so the deal |
|
| 81:07 | that this because this one is slower this one. This arrival is happening |
|
| 81:13 | . And uh we have a dozen up. This pair. We can |
|
| 81:18 | this one moving out across this array a consecutive time delay. It will |
|
| 81:24 | a linear move out through the array receivers at the p wave velocity. |
|
| 81:32 | then the same on the same wiggles see this signal moving out at the |
|
| 81:37 | wave velocity. So you have a receivers here. And you can see |
|
| 81:42 | shear wave arrival moving out linearly with share with box. And then as |
|
| 81:49 | pulled up the two up the um pull the tool up the the |
|
| 81:57 | They do clever processing so they can and find the interval velocities in each |
|
| 82:02 | about uh highest resolution they can get about the distance between these two |
|
| 82:11 | Like I said, normally there'll be dozen or more receivers up here. |
|
| 82:15 | that's that allows them to do ray processing. Not great processing but a |
|
| 82:21 | process. And that they can usually uh these slower philosophies even in the |
|
| 82:29 | of these fashions. Okay, so is the standard um sonic tool and |
|
| 82:35 | one has been in uh in operation uh I think uh 80 or 90 |
|
| 82:44 | and it gets better every few Uh the two companies make some kind |
|
| 82:50 | improvement and now that these things have worked well but there's a problem and |
|
| 82:57 | called the slow share problem. And happens if the formation slowness formation sheer |
|
| 83:07 | in here is less than the p velocity in the mud. In that |
|
| 83:15 | the refracted p wave is gonna refract from the bar hall access. Here's |
|
| 83:23 | refracted p wave of course this VP the formation is going to be bigger |
|
| 83:29 | VP in the mud but it could that V. S in the formation |
|
| 83:33 | great event is less than uh VP the mud. Let me say that |
|
| 83:40 | . Of course VP in the formation greater than V. P. In |
|
| 83:44 | mud. But it might happen that . S. In the formation less |
|
| 83:49 | VP in the mud. In which this thing refracts away from the borehole |
|
| 83:54 | . This is and that's also through and you're never gonna have in this |
|
| 84:00 | a critically refracted shear way like you here because in all cases it's refracting |
|
| 84:08 | from Warhol Access. So um to with this situation, they invented the |
|
| 84:19 | pole tool about four years ago. so what this tool does is it |
|
| 84:26 | the borehole wall with the positive Wave pulse this way and at the |
|
| 84:30 | time it sucks uh it sucks fluid the tool, making a negative p |
|
| 84:41 | pulse on this side. So it the borehole wall sideways and pulls the |
|
| 84:46 | heart full sideways, deforms the And so this Torsella wave travels up |
|
| 84:52 | bar hall and then it gets received di paul receivers up here which which |
|
| 85:00 | designed to to detect this kind of deformation. Personal wave travels up more |
|
| 85:11 | and vibrates sideways and it goes at distortion Allele mode travels with a velocity |
|
| 85:20 | is a little bit slower than the than the body wave velocity. Body |
|
| 85:25 | shear wave velocity in this and so know how to convert uh distortion wave |
|
| 85:32 | into the body wave velocity. And what they report by the way, |
|
| 85:37 | this uh torching away uh travels with it, which is frequency dependent because |
|
| 85:48 | the world, the borehole is this . So the um long wavelengths are |
|
| 85:55 | travel with a different philosophy in the run. Yeah, so you can |
|
| 86:03 | of take the inversion of these arguments apply, that's the case where plane |
|
| 86:09 | her incident upon a curved reflector. that in this case you don't necessarily |
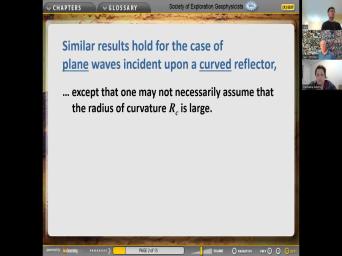
|
| 86:16 | that the radius of curvature is Make radius of curvature might be small |
|
| 86:21 | you uh you know, just depending how curved that reflector is. And |
|
| 86:29 | , normally the reflector has two radius curvature, kind of like a |
|
| 86:35 | Uh You try you know that saddle in insurance saddle? Okay, |
|
| 86:45 | uh the specialized word, I wasn't if you knew that word, but |
|
| 86:51 | for a saddle you have one radius character uh crosswise to the horse and |
|
| 86:57 | one another radius of curvature along the . And so uh the same way |
|
| 87:04 | in general, you can expect that matter how complicated the curvature is and |
|
| 87:10 | curved deformed sedimentary interface can always be described as two orthogonal radius of |
|
| 87:23 | Uh Coming from this, we're gonna focusing or d focusing, which we're |
|
| 87:31 | to discuss further in less than Uh but before that um uh let's |
|
| 87:38 | a little quits. So back to problem of curve rations. It says |
|
| 87:45 | don't care if the incident wave is or not since an exploration geophysics plane |
|
| 87:50 | are an acceptable approximation. I'm gonna that false. Uh two reasons. |
|
| 87:58 | , uh, when we have the critical reflections that we just talked about |
|
| 88:04 | the break and then also in the sonic organ contact. That's also question |
|
| 88:18 | . Even if the incident wave is plane wave approximation to the reflectivity, |
|
| 88:25 | critical is usually sufficiently accurate if you're than a couple of wavelengths from the |
|
| 88:31 | Stephanie, is that one true or ? Um this one would be |
|
| 88:42 | Yeah, that's true. Matter of , I showed you the correction factor |
|
| 88:46 | the correction factor goes to one as as you get more than one or |
|
| 88:51 | wife away from this Question three For reflecting interface. The maximum offset which |
|
| 89:01 | having your data may allow for maximum ankles, which are beyond critical so |
|
| 89:07 | these post critical headways are recorded on shallower interfaces. Even if they're not |
|
| 89:14 | at deeper interfaces. Stephanie, is mature fonts. Okay, that's |
|
| 89:20 | Although we normally uh, ignore them they're in there, they're in the |
|
| 89:25 | , they're on our service and maybe could give us useful information if we |
|
| 89:31 | look at them with intention. Maybe could learn something about those shallow |
|
| 89:37 | Now, maybe we don't really but maybe we do. You |
|
| 89:41 | it might be that there is uh in the shallow uh overburden above what |
|
| 89:49 | thought was our target horizon. Uh designed our survey to properly image that |
|
| 89:55 | horizon, but who knows what's in overburden. It might be worth our |
|
| 89:59 | to think about it. In the these post critical reflection post critical reflects |
|
| 90:10 | an interface with the faster formation below slower information above blah blah. We've |
|
| 90:16 | uh three statements and then all of above. So uh Stephanie, let |
|
| 90:21 | hear you talk your way through B. And C. Um |
|
| 90:31 | So a contains reflected head waves not in three critical reflections. That's |
|
| 90:42 | Yeah, that's true for all the we see. So so now we've |
|
| 90:47 | a problem. If we find even more of these uh which is |
|
| 90:52 | then we're immediately gonna default to But let's go through it. Uh |
|
| 90:57 | with B. Let me hear you away here. You talk your way |
|
| 91:01 | B. Have wave forms which are shifted from the incident wave. That's |
|
| 91:07 | as well, isn't it? that's true as well. Of |
|
| 91:09 | Well done. So we're now suspecting answer Indeed, but let's uh let's |
|
| 91:16 | C. Just to make sure have decreased by the geometrical spreading associated with |
|
| 91:22 | longer path fleets? Yes. Ok. Number. Good question |
|
| 91:29 | These post critical reflections rarely occur in sonic sonic content France. Yeah, |
|
| 91:38 | false because they normally occur. okay. So um that brings us |
|
| 91:44 | the end of this uh part Uh So you know if you were |
|
| 91:53 | this course with this name from some professor, we might stop here and |
|
| 91:59 | might have spent a lot more time these previous um topics. We might |
|
| 92:05 | gone more into the practicalities. But got me instead of that guy. |
|
| 92:11 | uh what we're gonna do for the of our time is look at uh |
|
| 92:19 | from keeping these same assumptions and then we're gonna relax those assumptions and important |
|
| 92:28 | to deal with rocks to deal with elasticity and to deal with an |
|
| 92:34 | So as so what I'm gonna do stop sharing here and bring up my |
|
| 92:57 | around a little bit next style. we go. Alright here it |
|
| 93:31 | Okay now I am going to bring zoom and I'm gonna share the screen |
|
| 93:44 | show you this file. So you be able to see the um introductory |
|
| 93:53 | for less than seven. Yes, . A presentation. Okay, so |
|
| 94:05 | . So um you can imagine that lots of complicated issues that we haven't |
|
| 94:11 | yet. And so now we're going discuss a subset of them. I |
|
| 94:15 | we could go on forever but uh just gonna to discuss a substance so |
|
| 94:23 | gonna be able to understand and explain and uh furthermore they can either confuse |
|
| 94:31 | interpretation or improve it depending on how ideal, you're gonna know what a |
|
| 94:41 | is, you're gonna know what a zone is in particular, you're gonna |
|
| 94:46 | how to pronounce that. That's a name. And you know the french |
|
| 94:51 | things differently than us. And so pronounced without the S. So um |
|
| 95:01 | is always a big issue. Uh always tell us the physicist we need |
|
| 95:07 | resolution, we need more resolution. when we give it to them, |
|
| 95:12 | not happy because uh of the subsurface be really complicated. Uh But we |
|
| 95:19 | to talk about some important ideas about and then we're gonna do more about |
|
| 95:25 | reflectors. And so here is the time. So these are the direct |
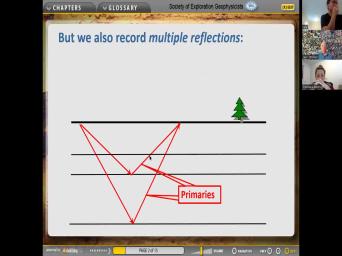
|
| 95:32 | here. We talked about the direct arrival and then the direct arrival |
|
| 95:38 | Uh and I guess we call this . Never mind the fact that I'm |
|
| 95:43 | retracting here. This is just a . Now we also record multiple |
|
| 95:49 | So these are these are two different . But then also in this situation |
|
| 95:55 | is a multiple where the energy goes up, down, up and gets |
|
| 96:00 | here after three bounces instead of And this one is uh this um |
|
| 96:08 | what we call a surface related multiple the the uh the balance downward is |
|
| 96:15 | at the surface. And furthermore if happen to have, if we happen |
|
| 96:20 | have a receiver right here, we record this and we call that a |
|
| 96:24 | wouldn't have a receiver here when it's over here. It's multiple. Here's |
|
| 96:30 | internal internal multiple. Whereas the downward happening off of some interior interface and |
|
| 96:37 | never did record that. Now here a symmetric multiple and here is an |
|
| 96:50 | . So in both cases the reflection in the surface. This one uh |
|
| 96:59 | uh asymmetric for obviously asymmetric. Now have what we call long period multiples |
|
| 97:13 | it's called long period. That's not good name, but that's the name |
|
| 97:17 | used to that. And what it is there's a long delay between this |
|
| 97:22 | arrival and this multiple arrival because The selection happens a long ways away from |
|
| 97:30 | from the two upper here's a by is a short term multiple where this |
|
| 97:38 | the light is not too much and really should call it a long delay |
|
| 97:44 | long and short delay, but only of short. Yeah. So here |
|
| 97:51 | have uh the simplest way Of reducing multiples out of our data invented a |
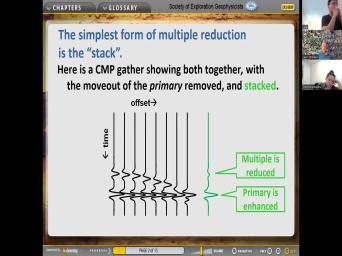
|
| 98:02 | time ago, probably invented in the . And it's the normal move out |
|
| 98:09 | . So here is a common midpoint trying primary reflection with move out. |
|
| 98:16 | this wave look here uh in the is exactly the same as this and |
|
| 98:24 | is a multiple with a slower move philosophy. You can see here this |
|
| 98:28 | move out uh moves out, moves more than the primary, let's go |
|
| 98:38 | here is the primary has only changed uh arrival time by this, March |
|
| 98:47 | . This this mark move on. changed, it's ruled out more but |
|
| 98:54 | arrival time is earlier. So that first let me say so. So |
|
| 99:03 | is this slower has spent more of time than the primary did in the |
|
| 99:08 | formation where it's slower. And so why the uh the average loss is |
|
| 99:15 | . Here's both of them together. you see that I've made this diagram |
|
| 99:20 | that here's the multiple uh arriving earlier short offsets and at further offsets, |
|
| 99:28 | gets tangled up in the primary, superimposed linearly. And so right here |
|
| 99:37 | fully superimposed. So the wave front a lot different than this one |
|
| 99:43 | This is the same way we're here here. But uh this is by |
|
| 99:49 | way, do you know why the here has smaller amplitude? It's because |
|
| 99:54 | it's reflected twice more than this So each reflection makes a reduction in |
|
| 100:02 | . So that's why this one has applicant. So in the cartoon, |
|
| 100:11 | multiple interferes with the primary, this primary long offset but not startups. |
|
| 100:20 | , uh one of the clever ideas we had a long time ago is |
|
| 100:25 | correct the move out. Using the velocities in the surface subsurface. And |
|
| 100:31 | so now this uh gather has been and the primary has been flattened. |
|
| 100:37 | see the multiple didn't get flattened because multiple is traveling at a different philosophy |
|
| 100:44 | we flattened together with the right velocity line these all up. And so |
|
| 100:49 | we had them all together and divide seven whatever 246 divided by eight. |
|
| 100:55 | we get this one. And so can see that by that averaging |
|
| 101:01 | The uh primary looks good, primary like this here. No uh no |
|
| 101:11 | from the uh multiple. But the almost got wiped out. Why is |
|
| 101:18 | ? Because it was not flat. so these terms here, they sort |
|
| 101:23 | cancel each other out. Not but very well. So the primer |
|
| 101:28 | enhanced. They said that is the reason folks why we do acquisitions, |
|
| 101:41 | allows us to do to make common point gathers. We want to impact |
|
| 101:48 | reflectors multiple times with different angles of and then um move out correct the |
|
| 101:58 | so that all those add up the . And by the way you can |
|
| 102:04 | that in this uh diagram here, isn't any uh oh effect, all |
|
| 102:10 | amplitudes are the same and these amplitudes the same. So, uh amplitude |
|
| 102:18 | discussion that's not included. If there an Avio effect, that would maybe |
|
| 102:26 | one here, this one will be amplitude than this one. Maybe |
|
| 102:32 | maybe smaller depending on what kind of leo we have all those amplitude effects |
|
| 102:38 | are ignoring. Yeah that's why we it. Well look here and that's |
|
| 102:45 | good idea. But look here this uh another way to handle the same |
|
| 102:51 | center here. We've done exactly the process except that we we did the |
|
| 103:00 | out removal with the velocity uh suitable the for the multiple. So we |
|
| 103:07 | the multiple and we reduced the primary not eliminated completely. Number one because |
|
| 103:13 | bigger and number two because some of are still in there, these waves |
|
| 103:18 | not um exactly cancel each other but can see that if we wanted to |
|
| 103:24 | could uh good process today to enhance multiple instead of removing and if we |
|
| 103:33 | that we would gain different insights in uh so that's a good idea in |
|
| 103:43 | context. You should remember if you're data that removing multiples is a good |
|
| 103:49 | but also moving primary. Just a idea. And both of them lead |
|
| 103:54 | different under different insights concerning the So here's a quiz and so Stephanie |
|
| 104:06 | out here, there's no all of both. So um either all of |
|
| 104:11 | are true. Well um uh what hoping is that just one of those |
|
| 104:16 | true because they don't give me the of all of them. So I |
|
| 104:20 | to listen to you while you talk way through this, starting with a |
|
| 104:28 | not A is true. That's sort the definition in it. Okay so |
|
| 104:33 | go on to be if the subsurface literally even apply I mean not |
|
| 104:43 | Right. Yeah that's you are That's a special case where it uh |
|
| 104:48 | at the midpoint by symmetry. But is it uh where the uh the |
|
| 104:56 | multiples happen? Could be not Okay so that's good. It's going |
|
| 105:01 | see sees kind of the same as . It doesn't necessarily happen. Have |
|
| 105:07 | happen at the surface. Oh they they can just be whatever they |
|
| 105:20 | Really? Right. That's right. don't know about this little thing. |
|
| 105:25 | that one is wrong. So you right. Uh The answer is a |
|
| 105:32 | two. Let me hear your You let me hear you talk your |
|
| 105:36 | through this one multiples arrived. This false because they arrive after because they're |
|
| 105:48 | . Mhm. Be the multiples usually out faster. So know that ties |
|
| 105:55 | with a. Okay, how about . See the multiples usually move out |
|
| 106:04 | . Yes. So that means So we're hoping that d turns out |
|
| 106:09 | be false. What do you think muscles usually have larger amplitudes than |
|
| 106:17 | No. Yeah. Usually have smaller because they have more reflections in their |
|
| 106:23 | . Okay that's good. Um Number . Let me hear you talk your |
|
| 106:28 | through this one. The multiples are overcorrected. They're not overcorrected because they're |
|
| 106:39 | . Just like the other ones right Under corrected because we corrected with the |
|
| 106:45 | of the primary. Yeah. Okay go on. The number to |
|
| 106:51 | the characteristics of the primary then uncontaminated the multiple. Yes. Well to |
|
| 107:05 | I'm thinking that that might be true depending on whether the multiple is still |
|
| 107:14 | with the primary or not. Uh haven't guaranteed that we remove that interference |
|
| 107:21 | we flatten with the primaries. So gonna call that one um uh provisionally |
|
| 107:27 | . And I'm going to a better down below. So just for like |
|
| 107:33 | visual on being like just so I see it. That's kind of like |
|
| 107:36 | cartoon we were just looking at Exactly. Okay. Yeah that's exactly |
|
| 107:43 | the cartoon the after correction with after the primary. The multiple was still |
|
| 107:51 | at far often so it's gonna affect behavior. Okay. Yeah. And |
|
| 107:58 | the way uh the reason why the or term in the Avio um uh |
|
| 108:08 | equation that we talked about earlier. reason why that's so hard to determine |
|
| 108:13 | in my view it's because of uh interference with the buy multiples which we |
|
| 108:21 | not sufficiently uh got rid of. so uh you know that makes uh |
|
| 108:31 | interesting possibility. It means that if did a better job of multiple elimination |
|
| 108:37 | we could actually use that curvature term our analysis. Uh I am not |
|
| 108:43 | of anybody taking that approach of connecting view behavior with multiple removal. And |
|
| 108:53 | think that's a very far missing avenue research anyway. Go on. A |
|
| 108:59 | . See um they're not eliminated. they're eliminated if you're lucky. But |
|
| 109:12 | you uh if you don't if you if you're the normal geophysicist, you're |
|
| 109:22 | lucky enough to get the perfect And there's a whole subclass of us |
|
| 109:29 | are specialists in the multiple elimination. not one of them, but I |
|
| 109:35 | a number, a number of those among my friends guys and and women |
|
| 109:42 | they have much more clever ways of or reducing multiples than what we just |
|
| 109:50 | through here. But that's uh the of a more advanced course. |
|
| 109:58 | now there is one class of multiples has received special attention and those are |
|
| 110:05 | ones that have their their downward bouncing at the surface. So here is |
|
| 110:15 | marine uh cartoon where we have receivers along here and we're receiving a primary |
|
| 110:21 | this uh on this event. We're uh and uh we're also receiving multiple |
|
| 110:30 | this event. But look, we that multiple right here. Uh and |
|
| 110:37 | we didn't put this receiver here to the multiple. We put it there |
|
| 110:42 | record the primary from a shorter But look what we got the multiple |
|
| 110:48 | in here. And so uh the thing here is that uh we can |
|
| 110:58 | the surface weighted multiples without even knowing is the velocity structure in the and |
|
| 111:04 | overburden. We don't know how to what is the velocity structure in |
|
| 111:09 | Um And we can still eliminate, can at least reduce it uh Anyway |
|
| 111:17 | this is uh uh due to a of ideas uh promoted most vigorously by |
|
| 111:26 | . U. H. Colleague Arthur . And you might be uh confused |
|
| 111:32 | has not seen his name on the list. Uh And uh the geology |
|
| 111:38 | , he's in the physics department. , so this technique is called surface |
|
| 111:45 | multiple elimination because in in a instance can actually eliminate them S. |
|
| 111:52 | M. E. It requires that record the balance everywhere. Well we |
|
| 111:57 | afford everywhere but we do a pretty job in for two D. |
|
| 112:03 | Like you say, we don't have uh in the marine environment, we |
|
| 112:07 | have receivers everywhere, but we have spaced every 50 m apart or so |
|
| 112:13 | that's pretty close to everywhere, but think about it in uh in a |
|
| 112:19 | D. Survey uh we have the line spacing is less dense. So |
|
| 112:25 | imagine uh Simple Marine Survey with one and one source behind the boat and |
|
| 112:36 | streamers. So you know, they clever ways to mhm directly behind. |
|
| 112:48 | might be ways so that it might 100 m or 200 m between streamers |
|
| 112:58 | and then they might be 10 km . And so they drag this whole |
|
| 113:04 | stream of receivers through the water. the cross line separation off line spacing |
|
| 113:13 | always less less dense spacing cross line in line because if you try to |
|
| 113:22 | it uh you know spacing cross line of only 50 m, you're probably |
|
| 113:29 | get the screamers tangled with each So uh normally the cross line spacing |
|
| 113:35 | much bigger. So that makes problems three D. Um implementation. |
|
| 113:45 | so now S army uses a nonlinear of scattering theory, which does not |
|
| 113:53 | knowledge of the service service velocity That is when you record those |
|
| 113:59 | that gives you enough information to eliminate , even if you don't know the |
|
| 114:08 | . So usually starts from the wave . Here's our wave equation does not |
|
| 114:14 | from the equation of motion. Under equation of motion uh has this additional |
|
| 114:21 | . And that comes from the fact in the subsurface, this um um |
|
| 114:28 | cancer does in fact depend on position the subsurface is in in homogeneous, |
|
| 114:36 | there's always a term here. And that term is not included uh in |
|
| 114:42 | S army algorithm. So the S is not completely general and in practice |
|
| 114:51 | um they are mhm. But it's standard way i there's a standard way |
|
| 114:58 | uh funding reducing sometimes even eliminating surface most. So why is this |
|
| 115:10 | We've got three answers plus all of above. Uh So Stephanie talk your |
|
| 115:15 | through this. Um Okay so their are usually stronger. So that would |
|
| 115:27 | true. Yeah that is true because free surface is the strongest reflect going |
|
| 115:37 | be and then we have special techniques deal with them. So that's |
|
| 115:43 | And one of the special techniques is . Right. Yeah. Right, |
|
| 115:47 | good, that's good. Okay um let's now think about ghosts. So |
|
| 115:55 | is um cartoon showing the up uh of marine acquisition. And so from |
|
| 116:08 | source you see some of the energy down but also some goes up comes |
|
| 116:13 | and reaches the receivers a little bit this one. So if we could |
|
| 116:21 | it a shadow but they call it ghost and uh that's going to be |
|
| 116:26 | and it's gonna depend upon this towing , this going depth. So if |
|
| 116:32 | tow depth is 20 m, that's be a longer delay. Then if |
|
| 116:37 | towing depth is 10 m or five . And so um that in mind |
|
| 116:47 | gonna be in our marine data. also we have this receiver ghost now |
|
| 116:52 | uh you know, exactly symmetrical Now it's common that the streamers are |
|
| 117:02 | so with a different depth than the . So that means the time delay |
|
| 117:08 | is going to be different than the away here, I think I probably |
|
| 117:12 | um just this senior to show that Now the reflection coefficient of the free |
|
| 117:23 | is always a -1 for all So now um at a certain frequency |
|
| 117:31 | we're gonna determine just now at a frequency, the extra path length of |
|
| 117:36 | ghost is exactly one wavelength. So because of the opposite polarity given |
|
| 117:42 | it cancels the primary making a notch the spectrum at that certain frequency. |
|
| 117:48 | when you look at the, when look at marine data and take uh |
|
| 117:52 | spectrum of marine data, you always a notch in the uh in the |
|
| 117:59 | that is hardly any energy coming at special frequency. Middle of the notch |
|
| 118:06 | of that special frequency uh the ghost the parliament. So you can adjust |
|
| 118:17 | uh the frequency at which this notch by adjusting the depth of going. |
|
| 118:24 | if you have uh greater depth of means a longer time delay for the |
|
| 118:34 | and a lower frequency for the That's what it says in the depths |
|
| 118:42 | the source and the receiver are The corresponding ghost period is longer as |
|
| 118:52 | uh if time delay is very Uh as in an ocean bottom seismic |
|
| 118:58 | , that's handled differently because that multiple is not just a simple phase of |
|
| 119:05 | , but many cycles of uh uh wave ones in a deep water ocean |
|
| 119:14 | sandals. So definitely let me hear talk your way through this and notice |
|
| 119:23 | we got none of the above down . So read the, read a |
|
| 119:33 | , then we've got these continuations. in a towed streamer Marine survey assuming |
|
| 119:39 | the down going and upcoming rays have same angle of incidents. A the |
|
| 119:45 | ghost has the same delay as the ghost. That's false. Yeah, |
|
| 119:50 | the receiver ghost might be different depending how they might tell the receivers um |
|
| 120:01 | a different depth than the source. that was false or be a notch |
|
| 120:07 | the spectrum occurs at a frequency where depth of the receiver is able to |
|
| 120:11 | half of the wavelength at that That's false. Let's think here. |
|
| 120:23 | Yeah, that's clearly false because uh normal incidents that uh ghost is gonna |
|
| 120:34 | going not straight up and straight back but it's gonna be going at an |
|
| 120:40 | . So um uh and furthermore it's to be in a different angle depending |
|
| 120:47 | the offset to the receiver. So clearly false. But let's um |
|
| 120:55 | let's, I think this is through and specialized to um uh normal |
|
| 121:08 | Okay, so the normal engines goes up, half a wavelength up and |
|
| 121:14 | down. So it's one wavelength behind primary but it's got an opposite polarity |
|
| 121:23 | of the reflection coefficient at the service -1. So that sounds to me |
|
| 121:30 | for normal incidence. That would be . But your answer is um um |
|
| 121:37 | answer is technically for it. Well go on to make sure that that |
|
| 121:42 | is also false. Um If the to deeper the receiver goes, has |
|
| 121:50 | notch at a lower frequency. Wouldn't be true? Since that's always |
|
| 121:57 | So so the answer is C. and and maybe be with that |
|
| 122:05 | Okay. So now uh of course a question about how to eliminate this |
|
| 122:14 | of multiples. So if the what not late. So you see it |
|
| 122:22 | a lot of on this technique. . So the question is suppose that |
|
| 122:29 | the water surface is rough so that waves on the water that can happen |
|
| 122:35 | ? And now the question is, does that do to the S army |
|
| 122:41 | ? I'm thinking about that. I thinking so that's a really good |
|
| 122:48 | Never been asked me before. This not something that I'm very knowledgeable |
|
| 122:52 | What I'm thinking is if the surface rough, but it's everywhere rough in |
|
| 122:59 | same way. Um that uh that's . I don't think that we assume |
|
| 123:10 | the surface is a perfect marriage. think that uh I think that when |
|
| 123:15 | Wig line does his um analysis, doesn't care whether the surface is rough |
|
| 123:22 | smooth And furthermore, he doesn't care there's a big wave passing by the |
|
| 123:32 | and not at the midpoint. I think he cares about any of |
|
| 123:36 | Uh That's it. That's a good . The next time I uh talked |
|
| 123:41 | him. I'm gonna ask him that by the way you've been around for |
|
| 123:48 | years, do you know? Professional . So the next time you passed |
|
| 123:56 | in the hallway ask him about that I think that he's probably gonna confirm |
|
| 124:02 | guest. But he is what I say way more knowledgeable than me about |
|
| 124:07 | topic. It happens following question is because we can decide the death of |
|
| 124:15 | receiver and the shot source. So will we can control the notch filter |
|
| 124:26 | the frequency spectra. Right? So will prefer to uh uh place the |
|
| 124:36 | filter at low, bring low frequency the high frequency. Um Yes. |
|
| 124:43 | we wanted to either uh put that at a high frequency uh short period |
|
| 124:52 | long period depending on um our objectives further at the receiver. And so |
|
| 125:01 | down further at the reflector. So would say that in these days we |
|
| 125:10 | more concerned. Well so if we're about uh resolution then we want to |
|
| 125:19 | the notch uh longer periods uh so we preserve the high frequencies. But |
|
| 125:26 | we're concerned about image making, we a new appreciation which we didn't have |
|
| 125:33 | most of my career, we have new appreciation of the value of low |
|
| 125:40 | in making images. And so if uh if we have that foremost in |
|
| 125:49 | mind making good images, then maybe want to move the launch too short |
|
| 125:56 | shorter periods. So as to preserve long period, um, long |
|
| 126:04 | both frequencies in the data. I would say that the thing to |
|
| 126:10 | is to uh, have, um, at the beginning of a |
|
| 126:18 | , you want to think about what your objectives are and think about |
|
| 126:24 | , um, uh, whether you to have a long period notch or |
|
| 126:32 | short period. And I think it depend well the circumstances you might |
|
| 126:38 | you might decide one way for this and another way for the next |
|
| 126:43 | And you know, this kind of is uh, one where two physicists |
|
| 126:51 | been keen keenly to understand this for . And so there's a lot of |
|
| 126:57 | , accumulated knowledge and uh, the on the acquisition company, we're gonna |
|
| 127:07 | running the uh, acquisition. They'll something like, oh, we always |
|
| 127:13 | the sources that seven m debt. what we have learned from our |
|
| 127:19 | And of course these guys have a of experience, a lot more than |
|
| 127:23 | in the oil companies. When I us speaking from my history at an |
|
| 127:28 | and BP, uh, uh, and service companies look at a lot |
|
| 127:33 | data than guys in all companies. the service company guy is gonna |
|
| 127:38 | well, this is the way we it. And so, uh, |
|
| 127:42 | that point earlier in the project, a good idea to sit down with |
|
| 127:46 | guy and say, well, explain to me why you do it |
|
| 127:50 | way and why. Um, it's a good idea for this case to |
|
| 127:55 | something different. And normally they love kind of a discussion because they want |
|
| 128:01 | have a smart customer. It's awfully the issues with them. And so |
|
| 128:08 | a good thing to talk about. maybe for this project you'll decide, |
|
| 128:13 | it shouldn't be at seven m, be at 15 m or it should |
|
| 128:17 | at three m or whatever. You decide that this particular survey because of |
|
| 128:25 | we're expecting in this environment, we want to do something differently than they |
|
| 128:31 | do. And uh, here's another a few years ago, I think |
|
| 128:38 | was PGS invented a different kind of acquisition is off where they had to |
|
| 128:49 | one above and one below. So called that the over under. |
|
| 128:53 | and the reason for that was to in the notch and maybe they have |
|
| 128:58 | over and under source to, to in uh, the source notes. |
|
| 129:06 | uh, all kinds of ideas are it's an important problem. This, |
|
| 129:12 | , this issue puts a severe limitation the resolution that we can expect because |
|
| 129:22 | these Golf so much for the, much for the service. Let's talk |
|
| 129:29 | internal most. So here's an intern and we can't eliminate that in a |
|
| 129:36 | way as we do with S. . M. E. Because we |
|
| 129:41 | record this what give up yeah because can use the wave equation to downward |
|
| 129:50 | the wave field so we record up and so if we know the velocity |
|
| 129:54 | here we can deduce and we know wave equation and everything so we can |
|
| 129:59 | what the uh what the data would like if we had receivers down |
|
| 130:09 | It's not perfect because we never know velocity here perfectly. For example we |
|
| 130:17 | know uh the velocity in all the here perfectly. We're limited by resolution |
|
| 130:23 | so on and furthermore we don't know anti socks. Be up here. |
|
| 130:30 | uh probably and I said topic but probably don't know that perfectly well so |
|
| 130:37 | we downward propagate we're going to not . Exactly. But let's um um |
|
| 130:44 | that possibility for now. And uh um assume that we can do |
|
| 130:54 | So we can compute the data that would have received down here and so |
|
| 131:00 | we can apply s army and also we we also have to know which |
|
| 131:07 | deep do we want to go do uh when we do this we're gonna |
|
| 131:11 | able to eliminate this one but still others that we did not eliminate by |
|
| 131:15 | technique. And so it will be for every surface and we're obviously not |
|
| 131:21 | do it for every surface. Um so uh now when we if we |
|
| 131:31 | this internal multiple here there's gonna be internal multiples from other interfaces which we |
|
| 131:37 | eliminate. And so it's not an problem means. So uh Stephanie, |
|
| 131:49 | let me hear you talk your way this. We got a B. |
|
| 131:54 | of the above and D. So me hear your Okay. Um Which |
|
| 132:05 | these statements are true. A salt interfaces are usually strong generators of internal |
|
| 132:13 | . Yes. Yeah. So now didn't teach you that, did |
|
| 132:17 | But because you are smart, you out from your common sense uh that |
|
| 132:24 | there's a big inner a big contrast uh uh an interface uh internal interface |
|
| 132:33 | gonna make multiples. And so this a good case where there's a salt |
|
| 132:39 | interface. And so it's gonna make multiples and we're frequently going to have |
|
| 132:45 | deal with. So good on you on. Number B. Internal multiples |
|
| 132:51 | always symmetrical. As shown in the . I feel like always is a |
|
| 132:56 | word. Yeah, always is a word. Right? So uh and |
|
| 133:00 | always a strong word. So uh that was going to be false because |
|
| 133:05 | going to be false. Uh And how about Dean? I would say |
|
| 133:15 | . Yeah, so they can be in many cases following the arguments that |
|
| 133:21 | gave back here, they're probably gonna be eliminated, but uh this one |
|
| 133:27 | we did find that this one is . So yes, okay, now |
|
| 133:33 | is interesting, this is friendly So all of the multiples that we've |
|
| 133:38 | about before we can say they're unfriendly they don't, they make troubles. |
|
| 133:46 | is possible that if you adjust your so that you reliance the so that |
|
| 133:53 | amplifier so that you enhance the multiples can that can be a friendly thing |
|
| 133:59 | do. Um wow normally multiples are as a nuisance and we want to |
|
| 134:10 | rid of but here are some friendly . How about this? Yeah. |
|
| 134:17 | off here in normal sub sequences there many interfaces closely spaced. Each |
|
| 134:25 | every one of them reflects some energy . And this the scattered wave field |
|
| 134:32 | upwards is partially scattered back gallons by near back interfaces above this twice scattered |
|
| 134:43 | has on average the same polarity as primary so they reinforce each other with |
|
| 134:49 | small delay. Hence they're called Friendly Nous. This concept was uh given |
|
| 134:57 | Nigel Anstey, one of the great of the previous generation. Still alive |
|
| 135:04 | well retired by now and you I do not know majority. Um |
|
| 135:11 | is the only important paper he ever and I think he was probably a |
|
| 135:17 | all company geophysicist and Anthony was a and they worked together on this but |
|
| 135:22 | sure the brains behind it was answered one of these uh multiples has a |
|
| 135:31 | attitude because it's been scattered twice once here once here and it follows along |
|
| 135:39 | the primary with a small delay. but it has a small aptitude. |
|
| 135:43 | when thousands of these reinforced together they most of the energy out of the |
|
| 135:50 | . And what you see on your are the multiples. How about |
|
| 135:54 | So I have here a diagram. this picture is oversimplified and lots of |
|
| 136:01 | . For example, there's no refraction , no conversions or nothing, but |
|
| 136:06 | want to talk about this. So this thing is going down, some |
|
| 136:11 | the energy gets reflected back up here then back down here follows along the |
|
| 136:17 | the uh primary with the smaller attitude a little delay coming from this two |
|
| 136:26 | travel here. And the same thing happening here and the same thing is |
|
| 136:29 | here. And if thousands of these , they superimpose constructively because they have |
|
| 136:35 | same um uh they have the same polarity and they just have a little |
|
| 136:46 | . That's what it says is supposed but delayed and the same thing happens |
|
| 136:52 | the way up. But look this is the primary without those friendly |
|
| 137:04 | . When it gets stopped here, doesn't have very much attitude because |
|
| 137:08 | most of the amplitude has been taken of it bled out of it by |
|
| 137:13 | with these interfaces. And so these um propagating along behind the primary uh |
|
| 137:22 | super posing not exactly, but each has its own delay. So they're |
|
| 137:27 | broaden the waves and that's what you on your workstation. Look at |
|
| 137:34 | there's Nigel Anstey himself a few years when he was honored by the E |
|
| 137:39 | G in Amsterdam. And I made my business to get in this picture |
|
| 137:45 | these famous guys, here's Nigel here's Anders Robinson, you've heard his |
|
| 137:50 | , He was uh one of the of digital seismic processing back in the |
|
| 137:55 | . Here is Claus Helberg, another previous generation, about 90. |
|
| 138:02 | um uh Nigel was about 90 of . Nice beard, don't you |
|
| 138:08 | And this guy is somewhat younger, guy is named Zhukovsky, Famous guy |
|
| 138:12 | uh del from uh University of Edinburgh in Edinburgh. And I saw him |
|
| 138:22 | this week in uh in Houston and asked him how is Nigel getting |
|
| 138:26 | And he said uh as of he was in good health. So |
|
| 138:31 | two correspond exchange. So uh I this opportunity with all these great |
|
| 138:38 | I just stuck myself into the picture I had my wife take pictures. |
|
| 138:42 | there it is and this is sort a Ray theory explanation of what goes |
|
| 138:48 | and that's the way Nigel did He was very good at explaining complicated |
|
| 138:56 | in terms of of pictures, like one I just grew a better way |
|
| 139:04 | describe that is in the wave theory in this case we want to use |
|
| 139:10 | equation of motion for in homogeneous Just like we showed this formula a |
|
| 139:15 | minutes ago. So uh if this varies with uh with position, like |
|
| 139:24 | says here, then this derivative is make a term like this. So |
|
| 139:31 | part of it gives the wave equation this part gives uh an additional term |
|
| 139:36 | we should not we should not neglect term because of the many, many |
|
| 139:45 | sedimentary interfaces in the sub surface. there's more discussion about this in less |
|
| 139:51 | nine. So we're here on less seven. So we still have a |
|
| 139:55 | to go. Let me show you data. This is from A |
|
| 140:01 | And in the VSP you have a of receivers in the borehole source on |
|
| 140:08 | surface. And you can actually record down going wave field. This is |
|
| 140:13 | director rifle is going down. Um as it's going down uh Spectrum is |
|
| 140:26 | look like this. So the first , this is uh at a shallow |
|
| 140:33 | and this is a deeper and deeper deeper receiver. Okay, and so |
|
| 140:38 | is uh this shallow receiver is at certain depth. So this um trace |
|
| 140:45 | at 7/10 of a second. So it goes down twice as far to |
|
| 140:51 | how the traces look very different. you can see that this one here |
|
| 140:57 | a lot less high frequency in it this one. Here's uh down after |
|
| 141:05 | seconds. And it has broadened out lot. And after 3.5 seconds, |
|
| 141:10 | 5.5 seconds. It's broadened way out , so make uh so this is |
|
| 141:17 | 100 milliseconds here. So this is a broad waves and you can see |
|
| 141:23 | we lose the high frequency information as go down. And the reason is |
|
| 141:28 | all of these friendly multiples to propose each other with different delays and that |
|
| 141:36 | destroys the high frequencies as you can right here with your eyeball. So |
|
| 141:47 | take the spectrum here. So we 123 spectrum. So here is |
|
| 141:53 | the spectra from the shallow receivers and is the deepest one in the solid |
|
| 142:00 | not the deepest one, but 2.7 . It didn't show even show the |
|
| 142:05 | one, but the 2.7 seconds um the spectrum is here and you can |
|
| 142:11 | that that we've lost a lot of frequencies from the shallow receivers down to |
|
| 142:18 | evening. Of course, all of are normal, that they have the |
|
| 142:23 | amplitude here at this frequency. following this argument, the primary eventually |
|
| 142:33 | most of its energy to these friendly . That's free, is friendly. |
|
| 142:40 | uh given by Nigel Anstey and they them friendly because they do reinforce each |
|
| 142:49 | . What we actually detected what we on our on our workstations is uh |
|
| 142:57 | we call the primaries are really the superposition of all the friendly most of |
|
| 143:04 | . And the true primary is just first initial, the the very initial |
|
| 143:12 | uh emergence of the of the So if you if you see a |
|
| 143:18 | separated arrival, yeah. First very part as it deviates from zero, |
|
| 143:26 | the primary and welcome. The Is these friendly mountains. Now, |
|
| 143:33 | is the velocity of that? Um Finally multiple package travels with a velocity |
|
| 143:43 | by the back of average. Now me think here. I don't |
|
| 143:54 | Yes, I think it's true. we talk about the back of average |
|
| 143:59 | the first or second lecture. Did do that? Let me I don't |
|
| 144:10 | so. Oh no we did So we're gonna do that directly. |
|
| 144:16 | . Okay. So uh so we ourselves what is the velocity of uh |
|
| 144:28 | package of friendly and multiple super posed , which we call the primary. |
|
| 144:33 | really it's it's a superposition of all friendly most. It's going to be |
|
| 144:38 | than the rain theory average of the of losses. So here's the |
|
| 144:42 | Uh Consider the vertical velocity is a period waves. So here's a cartoon |
|
| 144:47 | sedimentary layers. And uh here we the velocity law. It's got alternating |
|
| 144:54 | of high and low high and low and all this of course bedded sedimentary |
|
| 145:00 | . And why is of course because gonna hit this from below with a |
|
| 145:05 | frequency wave, how to announce high because these are successive wave fronts. |
|
| 145:10 | so these wave, let's these this here is less than the player |
|
| 145:19 | So we call it a short period . And here's our receivers up here |
|
| 145:22 | we ask yourself the question when we the transmitted wave, what was the |
|
| 145:27 | of this wave? Okay, so work it out. Uh So we're |
|
| 145:35 | define the velocity as the total thickness by the total travel time. Pretty |
|
| 145:40 | . And then we're going to uh the total thickness as the sum of |
|
| 145:45 | the layer thicknesses and the total travel is the sum of all the travel |
|
| 145:49 | . Pretty obvious. And now we're to eliminate the times in favor of |
|
| 145:56 | thickness divided by the velocity in each . Okay now we're gonna invert the |
|
| 146:03 | thing at the universe of this. now on the right hand side we |
|
| 146:08 | the sum over layers of the layer divided by the slowness, at times |
|
| 146:14 | layer velocity times the slowness which is same as divided by the velocity in |
|
| 146:20 | layer. So and then we're dividing by the sum of the layer thickness |
|
| 146:27 | this one. And this is the of this. And so that looks |
|
| 146:32 | a weighted average, a weighted And what are the weights, the |
|
| 146:37 | of the layer thicknesses. And so are the sum of the weights. |
|
| 146:41 | that's just a weighted average and we're uh you know that with angle brackets |
|
| 146:46 | that and what is being uh what being averaged? It's the slowness in |
|
| 146:52 | layer, that's what's being average, what uh that's uh rotation. |
|
| 147:02 | now that's all pretty obvious. So, uh so now, how |
|
| 147:07 | the vertical velocities for long period This is the seismic problem. It's |
|
| 147:13 | same um layered sequence, same And now we're hitting it from below |
|
| 147:19 | a long period waves. How do know this is a long period because |
|
| 147:23 | period of this distance between successive wave is longer than the layer things. |
|
| 147:33 | so it's gonna be emerging here and looks like a different maybe like |
|
| 147:38 | that's gonna come out out of the to then we're gonna um detective that |
|
| 147:49 | velocity in this case there's a thin case. So this is all the |
|
| 147:57 | layer case because the wavelength is long to the thin beds. So this |
|
| 148:02 | layer case. This is given by what we now call the backers |
|
| 148:08 | And uh um that's a bit of a disservice to the guy who really |
|
| 148:17 | this for the first time, who a guy named Brueggemann living in Germany |
|
| 148:22 | he had the poor judgment to uh this in german just before the |
|
| 148:28 | so nobody remembers Brueggemann. And when uh discovered it independently, 25 years |
|
| 148:36 | , he gets all the credit. in our business there are two Baptists |
|
| 148:41 | brothers. So there's George Baptist and backers. This is George Bacchus and |
|
| 148:47 | was a very mathematical guy who worked slumber. Uh and uh very mathematical |
|
| 148:54 | my old baptist was a very intruded and he was a professor at the |
|
| 148:59 | of texas and he just died a of years ago and I think George |
|
| 149:04 | still alive. But George was not accused. George was really a |
|
| 149:13 | Uh and he was he was quite guy. I knew him well. |
|
| 149:18 | was a former president of the scg professor at the University of texas and |
|
| 149:25 | died Apple music. So now let's at the formula. It's a terrible |
|
| 149:30 | formula. You see we have in upon in verses, we got square |
|
| 149:34 | and we've got squares and we got density appearing explicitly. So this is |
|
| 149:42 | real mess. That's what bank has it for me. You can look |
|
| 149:47 | this paper famous paper and we want compare that with the coarse layer of |
|
| 149:53 | which we just uh looked at previous . Very simple intuitive. So the |
|
| 150:00 | our velocity is the inverse of the of the Florence. Yeah. Um |
|
| 150:13 | do we call this rate there? remember rate, there is the high |
|
| 150:17 | approximation. So of course the problem that layers of coarser than the |
|
| 150:24 | So that must mean high frequency. what is the relationship between these two |
|
| 150:32 | when you just look at it are to see a relationship. So before |
|
| 150:37 | talk about that difference let's go back uh the derivation of the course |
|
| 150:43 | Uh of course layer problem and exactly we showed before. And I'm going |
|
| 150:54 | ask you is where in this which I know looked very straightforward and |
|
| 151:01 | obvious. Every step was an easy . We've got all the steps out |
|
| 151:05 | . Where did we assume? How ? So I'm gonna stop here and |
|
| 151:11 | me think about that both of This is not obvious. So think |
|
| 151:16 | that a while and then I'm gonna you, where did we assume in |
|
| 151:20 | derivation? Where did we assume? frequency. So you tie tell me |
|
| 151:35 | did we assume how frequency? Um would say that the jab, I |
|
| 151:49 | see depth in here. Okay, so when we express the thickness as |
|
| 151:56 | sum of larry thicknesses, is that high frequency? That seems to me |
|
| 152:03 | just the geometrical argument. If we the frequency, the death will not |
|
| 152:16 | just a value range. So tell precisely on this slide where we um |
|
| 152:28 | we made a mistake is it? is it here is it here where |
|
| 152:33 | is it? No any hint I . Okay so this is where it |
|
| 152:45 | right there. So when we say the total travel time is just the |
|
| 152:51 | of the individual travel time. That that assumes that the way it goes |
|
| 152:56 | it's coming up, it goes through it goes through layer one and then |
|
| 153:01 | goes through layer two and then it through layer three and this animal all |
|
| 153:06 | and you get the total travel But if the wavelength is a long |
|
| 153:13 | , when the when the when the of the wave gets up into layer |
|
| 153:21 | , The body of the wave is in layer one and when the front |
|
| 153:26 | up to layer three, some of in layer two and some of it's |
|
| 153:29 | layer one. So what it does it compresses them all together And we |
|
| 153:35 | say that the total travel time is sum of individual times because that's not |
|
| 153:41 | way it works, it doesn't go one and then the other and the |
|
| 153:45 | it goes through them all together. so that's what uh back is. |
|
| 153:54 | uh it's not a hard paper to . I encourage you to look it |
|
| 153:58 | . And if you need to you ask me and I'll give you the |
|
| 154:02 | reference that you'll probably be able to it for yourself. And so uh |
|
| 154:08 | I'm gonna ask what is that? the relationship between this uh is this |
|
| 154:13 | bigger or this one bigger or And so to answer that question, |
|
| 154:18 | know, we can't answer it in direct way because it depends upon density |
|
| 154:23 | example. You see the density density here at all. So what |
|
| 154:27 | going to have to do is assume things. We're going to assume the |
|
| 154:32 | among the layers is small. And we're gonna do a taylor expansion of |
|
| 154:37 | . And then we're going to assume statistical relationship between density and velocity, |
|
| 154:43 | . We're going to assume the uh correlation between density and velocity, which |
|
| 154:49 | given by gardening, who was a professor at your age at price and |
|
| 154:58 | years ago. So when you do , what I just said, you |
|
| 155:04 | that the long wavelength philosophy, that's one is given by the short wave |
|
| 155:10 | times one plus a correction factor. the correction factor involves an average. |
|
| 155:16 | what these brackets mean. And what's averaged is the local uh local velocity |
|
| 155:23 | . Uh This is layer by layer variation and this is the average velocity |
|
| 155:28 | the whole stack. So we had non dimensional relation here. Now some |
|
| 155:35 | those individual layer philosophies are bigger than average and some are smaller. And |
|
| 155:42 | each one we take uh general velocity average walls. That's right. And |
|
| 155:50 | some of them are gonna be faster some are gonna be slower than the |
|
| 155:54 | . So some of these members are be positive, some are going to |
|
| 155:57 | negative, but we're spurring them So this is all positive, |
|
| 156:04 | And because of this minus son means the long way going to velocity is |
|
| 156:10 | than shortwave lost. So you um that's uh wave theory analysis yielding |
|
| 156:23 | same results as Angela Anstey Doherty and discussion of friendly multiples. So |
|
| 156:34 | you can think of this as sonic . And these are the seismic velocities |
|
| 156:41 | see from a circumcise mint. Now you have sonic logs and you have |
|
| 156:51 | band velocities from a surface seismic survey the same area, you might want |
|
| 156:56 | compare them. And so to calculate sonics with the sizing band, you |
|
| 157:01 | an extra step. You've got to perform this uh calculation. So this |
|
| 157:08 | what you need for size mix. is what you can calculate from a |
|
| 157:13 | log. Just doing that uh sonic averaging like I should before. And |
|
| 157:18 | can also calculate this from the sonic . And this is the friendly multiple |
|
| 157:24 | coming from the wave equation are coming the equation of motion. So to |
|
| 157:31 | so back us. When you derive equation of motion. When he arrived |
|
| 157:37 | baptist average loss started from the equation motion, which I showed you a |
|
| 157:42 | times all slides back and discussion more less and more so we can do |
|
| 157:55 | . But there are other issues to uh for example, uh the seismic |
|
| 158:01 | and the sonic waves sample different parts the earth. The sonic waves only |
|
| 158:07 | , sample near the bar hole in seismic wave was going down some distance |
|
| 158:14 | from the borough. And it's maybe to think that uh walks in that |
|
| 158:23 | in the two parts of the earth the same velocity. Furthermore, the |
|
| 158:29 | ways uh, maybe aren't giving me right answer, but maybe you need |
|
| 158:34 | do some sort of correction to deal borehole damage. I suppose when the |
|
| 158:41 | is when the drill bit, it's down through the rocks, suppose it's |
|
| 158:46 | . It's chewing up some of the and spitting them out. That makes |
|
| 158:51 | what it does to make an empty . And in the process, it |
|
| 158:55 | be putting cracks into the uh rocks the formation wall and those cracks are |
|
| 159:02 | there, um affecting the sign of . When you come back with us |
|
| 159:09 | logging tool, you might be sending sonic waves to damage formation, depending |
|
| 159:16 | the formation. Furthermore, the rock might be intrinsically different from uh, |
|
| 159:25 | uh, the sighting from the low frequencies in size in place. |
|
| 159:30 | you can have exactly the right the rock in the laboratory and measured at |
|
| 159:35 | frequency and low frequency, you might a difference. Should not assume that |
|
| 159:43 | is you. And so, here's another important point. If the |
|
| 159:51 | velocities come from, move out as to from the same vertical bsp. |
|
| 159:55 | might be affected by an because, know, uh for financial social see |
|
| 160:03 | that the rays are going through the and a weak angle sonic tool, |
|
| 160:09 | gone vertically. And so those might different velocities and so well more learn |
|
| 160:15 | about that unless Okay, so let me hear you talk your way |
|
| 160:25 | this. Okay. Individual friendly multiples have very small amplitudes since they are |
|
| 160:34 | . That's true. Be many, internal multiples super posed constructively to make |
|
| 160:43 | amplitude. Yes. Yeah, that also true from why? Going to |
|
| 160:54 | , oh that's what you said, um the friendly multiple arrival has a |
|
| 160:59 | velocity given approximately by the back is of the individual. Yes. |
|
| 161:08 | so that brings us to diffraction. me see here how we're doing with |
|
| 161:14 | . Okay, so it's 4:30 so us uh take a break here and |
|
| 161:21 | will come back to the fractions at . So see you in 15 minutes |
|
| 161:29 | 4:45 and I think what I'm gonna is to stop sharing and video. |
|
| 161:48 | don't know what I am doing wrong that when I first bring this |
|
| 161:53 | it does not um respond to the . So uh what I'm gonna have |
|
| 162:02 | do is like this. Um And , okay, now this works |
|
| 162:23 | so uh this is a really good taken from Sheriff and gil dark uh |
|
| 162:30 | shows about um uh what the fractions . So it's uh duty situation. |
|
| 162:39 | here we have uh soon to be variant in and out of the |
|
| 162:42 | And here we have a wedge in otherwise uniform body. And we got |
|
| 162:49 | coming in from the northwest like And so these waves which are way |
|
| 162:55 | board from the uh from the tip from the point, uh they are |
|
| 163:02 | by the point. And so you see here uh this is what the |
|
| 163:06 | looks like. Okay, now let's , let's look at various parts of |
|
| 163:12 | , there's the unaffected wave and here normal reflections. These are coming in |
|
| 163:18 | from here and reflecting off of Uh These wave forms look just like |
|
| 163:26 | wave forms and these are diffraction is at all this other energy. Uh |
|
| 163:35 | know, from here, around to in here, all these other, |
|
| 163:40 | are uh diffraction waves and you can that the wave forms look different from |
|
| 163:48 | incident wave forms. Uh and the gets changed, the amplitude sort of |
|
| 163:55 | , but it's not true that you a complete shadow. So you might |
|
| 163:59 | that there's a complete shadow, nothing all from here to here. Uh |
|
| 164:05 | of that's in the shadow, but not true, plenty of energy in |
|
| 164:13 | . And uh similarly from this point here, we get reflections in all |
|
| 164:20 | , not just back in the uh with these are reflections here off the |
|
| 164:25 | of this surface uh angle of reflection angle of incidence, but look at |
|
| 164:32 | these different angles here coming off of point. And with various aptitudes and |
|
| 164:38 | way for those are the fractions backwards all angles forwards at all angles, |
|
| 164:49 | the these defections smooth, smooth, smoothly where the undistracted way as you |
|
| 164:55 | more and more output. Okay, we want to apply that same idea |
|
| 165:04 | this context of imaging. So here have um A block sitting on top |
|
| 165:13 | a reflector and we're gonna show two of normal incidents acquisition Over here. |
|
| 165:22 | this one goes through the middle of block and this one is outboard of |
|
| 165:26 | block at some distance and this is 150 m outboard of the block. |
|
| 165:33 | so these are zero offset traces along center line and so right over here |
|
| 165:39 | see a reflection from the base layer and the same thing over here and |
|
| 165:46 | is a reflection from the top of block. But look right here, |
|
| 165:51 | are other energy coming off of this being reflected back this way. So |
|
| 165:58 | is a normal incidence trace taken right . Source and receiver at the same |
|
| 166:03 | just outboard here, right about here it's receiving energy not only reflected energy |
|
| 166:10 | the base, also deflected energy off this edge and over here is the |
|
| 166:16 | sort of thing. Maybe I can that better. So so here is |
|
| 166:20 | is a receiver. This is a from a receiver which is just above |
|
| 166:25 | point. It's up here some and can see that it's getting re fractions |
|
| 166:31 | that edge. Now, here's something to look at down here is the |
|
| 166:41 | of the block. So uh evidently velocity in the block is different than |
|
| 166:48 | velocity in the base down here. there's an impedance difference uh right at |
|
| 166:54 | base of this block. And so can see that right here. It's |
|
| 167:01 | simple because you see what the waveform like, it looks like uh trough |
|
| 167:07 | , you know, peak trough, , that's not exactly what we see |
|
| 167:12 | , but maybe it's uh here we peak trough, no peak down |
|
| 167:19 | So these wave forms are somehow I don't know what accounts for that |
|
| 167:25 | . Uh Yeah. Now, let's at similar traces taken along this |
|
| 167:34 | which is outboard of the block. here is the uh reflection from the |
|
| 167:42 | all along here. And notice right here, those are the fractions coming |
|
| 167:49 | of this edge, even though it's away from the line of acquisition. |
|
| 167:55 | Some of the because this is uh raised, see uh the waves are |
|
| 168:02 | from sources above here somewhere. Uh looks like it's approximately drawn to |
|
| 168:09 | So the sources are up here. uh they're radiating in three dimensions and |
|
| 168:16 | of them are going out of the plane, hitting this uh corner and |
|
| 168:23 | back to a receiver on this vertical uh with zero offset. And so |
|
| 168:30 | see that that diffraction right there. , this is a portrait of |
|
| 168:47 | that's how this this name is pronounced . And uh that's his name, |
|
| 168:52 | an S on the end dutch And he thought of of reflections like |
|
| 169:00 | , he said that if you have incident wave like this, uh it |
|
| 169:07 | a reflection at every point along this along this reflecting plane acts like different |
|
| 169:16 | like we just said. So there's here, one here, one |
|
| 169:19 | one here etcetera. And each one those puts uh refracted way back |
|
| 169:26 | Uh not only in the uh the direction, but in all these |
|
| 169:34 | So, so uh so if there's diffract around here, it's putting some |
|
| 169:38 | over here, some here and some and some back here. And Hagan |
|
| 169:45 | that if you uh take a So all of these circles here, |
|
| 169:50 | comes up to the reflected waves from summation of all these diffraction points. |
|
| 169:57 | the mathematics for this turns out to just exactly what we talked about |
|
| 170:03 | Alternative way of looking at reflections. , um uh there there are certain |
|
| 170:12 | here. For example, if this a D factor, it's also distracting |
|
| 170:16 | the other way, it's also distracting . So what about that? Mr |
|
| 170:21 | . Well uh I am not familiar why that doesn't work out, that's |
|
| 170:29 | a fatal objection, but I don't exactly why this is got the factors |
|
| 170:39 | . These two factors they should be in all directions. Now, this |
|
| 170:43 | an important point in um um in imaging, because there's a technique of |
|
| 170:55 | called turk off imaging, where uh Kirk off another german name, assumed |
|
| 171:04 | every single point in the subsurface might a diffract every single point. And |
|
| 171:10 | he uh added up the uh energy from every single point. And in |
|
| 171:20 | places they they superimpose constructively making for coherent arrival in other places they interfere |
|
| 171:30 | and wipe each other out and you nothing. And that is a way |
|
| 171:36 | uh produce an image out of um direct David. And so that's a |
|
| 171:45 | good idea actually, assuming that everywhere the surface there's a factor just like |
|
| 171:50 | talked about here, and uh where uh imaginary the factors result in a |
|
| 171:59 | event, that is actually a And there's another diffraction point just nearby |
|
| 172:06 | here, which reinforces that, and one reinforces that. And so that's |
|
| 172:12 | gives us reflections, awful minor Another way of formulating so um about |
|
| 172:27 | quiz, which of these are So we got three and then all |
|
| 172:33 | then just two of them are So um uh Stephanie was here, |
|
| 172:39 | talk your way through this all pd are caused by discontinuities of p velocity |
|
| 172:46 | the subsurface. I don't like the all in the front of it. |
|
| 172:53 | . Good for you, you're uh alert to uh exceptions. Uh So |
|
| 173:00 | . So how about uh how about where uh the velocity is the same |
|
| 173:08 | but there's a density discontinuity in the . That sure that we're good. |
|
| 173:14 | you are correct to be suspicious Okay. Uh Let's go on to |
|
| 173:22 | an elastic discontinuity acts like a source activated by an incident wave, radiating |
|
| 173:28 | in all directions with different amplitudes and that be true. Yeah. |
|
| 173:35 | I'll call that one true good. we got one false and one |
|
| 173:38 | So see better be false. So read it through and verify. Go |
|
| 173:45 | A ray which misses the pinch out a sedimentary wedge by more than 1/4 |
|
| 173:50 | is not affected by that pinch Well, we never said that. |
|
| 173:55 | , we we we never said And in fact if you look back |
|
| 173:59 | the at the figure which I started section with at that point. So |
|
| 174:06 | that was false. And so all have is being good. Okay, |
|
| 174:13 | funnel zones. Okay, suppose just that the reflecting plan is not |
|
| 174:22 | If it were perfect, you would um a reflection like this which we |
|
| 174:27 | spectacular reflection. But suppose that this down here is not uh polished in |
|
| 174:37 | laboratory, but suppose it's the result a sedimentary process. So in that |
|
| 174:42 | it might not be a perfect mirror it might uh energy from this uh |
|
| 174:51 | this mhm reflecting point might go back other directions in addition to this |
|
| 175:02 | So for an imperfect mirror you might um energy coming back made, may |
|
| 175:12 | different in energy coming back in all , including back towards the source |
|
| 175:19 | Okay. And that's what it says . If the reflector is import is |
|
| 175:25 | radiating wavefront sources right over here receives arrivals back in all directions included back |
|
| 175:33 | the source. Each of these articles delayed according to its path link of |
|
| 175:38 | . So the velocity is the same . But uh this uh wavelength, |
|
| 175:43 | path link is longer than this path . So there's gonna be a |
|
| 175:49 | So, now what that means is realistically seismic waves do not really respect |
|
| 175:55 | a point, but from an And so imagine here that you've got |
|
| 176:00 | imperfect mirror and a source point here we're gonna look at reception back at |
|
| 176:08 | cet reception. So it's a perfect , you only get uh energy reflected |
|
| 176:15 | from a but if it's imperfect then will be a zone around here of |
|
| 176:21 | certain radius, which we're going to out where uh reflections from inside |
|
| 176:29 | all add up constructively when they come here, even though it's not a |
|
| 176:35 | mirror. So that's called the first zone. And it's defined to be |
|
| 176:40 | circular area of which we see here uh the cross section uh and half |
|
| 176:47 | it obviously going to be another half here, and then in two dimensions |
|
| 176:52 | gonna be a circle in this but it's more fun to do this |
|
| 176:58 | two dimensions. Um uh So it's be a circular area around the speculator |
|
| 177:05 | point, which is here, it's have this radius and within which the |
|
| 177:10 | czar delayed uh are delayed Uh from one by less than 1/4 of a |
|
| 177:21 | . So um where does that 1/4 ? Well if if it's delayed by |
|
| 177:27 | half of a period then it Right? So so this 1/4 is |
|
| 177:34 | towards uh cancelation. So uh let's at some formula. So because I |
|
| 177:44 | said in the in the definition of first funnel zone, if the velocity |
|
| 177:49 | uniform, then it's just simple So this adept is Z. And |
|
| 177:56 | uh uh links here is Z plus over eight. And why is |
|
| 178:05 | Because if it's uh two way travel , it goes uh It's gonna be |
|
| 178:13 | over four Way with the report longer this one. And so what what |
|
| 178:20 | the length of this segment here? is the radius of the funnel zone |
|
| 178:26 | the other half of it is over for us. And just by a |
|
| 178:30 | uh that uh length of this is square root of uh my partners provided |
|
| 178:43 | the square root of the uh the side. So it's uh spanning this |
|
| 178:53 | . We have a length of uh is the first from Wellesone is given |
|
| 179:01 | Z times lambda Or four divided by over eight square. So uh it |
|
| 179:11 | comes from this from over here. so you can see that um Normally |
|
| 179:17 | have the depth is a lot bigger the wavelength. So normally we can |
|
| 179:23 | uh personnel zone by this first I just want to uh recapitulate |
|
| 179:32 | Why do we say we went over ? So uh wavelength over eight that |
|
| 179:40 | delay time, total uh total extra of uh wavelength number four. And |
|
| 179:48 | instead of wave went over to then would have opposite polarity and would have |
|
| 179:52 | . So for waves further out here began to uh interfere destructively. So |
|
| 180:04 | um all of these waves then, we have our source up here at |
|
| 180:11 | surface there. And what we just is that if this is not a |
|
| 180:15 | mirror, then we're gonna get um from all these various places back here |
|
| 180:24 | the surface, arriving with a little . But we're gonna arrive constructively and |
|
| 180:30 | gonna to propose constructively. And uh a little delay. And so of |
|
| 180:36 | that's going to broaden the wave Uh and this has nothing to do |
|
| 180:43 | friendly multiples that we just talked This is a new effect which broadens |
|
| 180:51 | the way of that. Now the says, what does this imply for |
|
| 180:55 | aptitude? So you can see right that oops, that's probably gonna affect |
|
| 181:03 | attitude that we that we receive up at normal incidence. Now, next |
|
| 181:09 | is, is this going to affect A. B. O. |
|
| 181:13 | um you can directly um extend these to finite social seaver offsets, which |
|
| 181:22 | what we normally are interested in. then you're gonna be thinking that from |
|
| 181:27 | from a a a circle, the of this uh with a source here |
|
| 181:34 | a receiver here, we're going to receiving distracted arrivals uh from everywhere in |
|
| 181:41 | , not just from the speculator reflection , and that's going to affect our |
|
| 181:47 | as a function of of offset. this is a complication to a |
|
| 181:58 | O. That depends upon just how this mirror is. Uh If we |
|
| 182:08 | a little uh suppose this interface represents difference between sand and shale in the |
|
| 182:18 | process millions of years ago. And supposed so, uh when that |
|
| 182:26 | it goes from sandy to Shelly. that means is the water has gotten |
|
| 182:31 | because of the shales are deposited in water and the sands are deposited in |
|
| 182:40 | water. And as uh water level and falls with geologic history. That's |
|
| 182:48 | causes the alternation between shales and So now this sends down here in |
|
| 182:55 | lower bottom when that was laid down , uh The water was shallow. |
|
| 183:02 | there might be ripples on this Sand, sand ripples. When you |
|
| 183:09 | to the ocean, you can see in the very shallow water, you |
|
| 183:13 | see them right away, I can them with your feet and so |
|
| 183:17 | And such things might get fossilized into rocks as the water level changes and |
|
| 183:25 | whole thing gets covered with shale. there's sand ripples down here and you |
|
| 183:35 | a right to ask, well, what's the what's the separation between these |
|
| 183:41 | marks? What's the that this is wonderful marks. You can see these |
|
| 183:47 | just examples of what sedimentary processes quite and do to make this a non |
|
| 183:57 | mirror. And you can see that the imperfections could be minor or they |
|
| 184:04 | be more significant. You just don't . So, if you were trying |
|
| 184:08 | model this, you would model this a foot with variable uh imperfections. |
|
| 184:17 | has some sort of parameter in here would measure the amount of imperfection of |
|
| 184:22 | mirror. And that would depend, example on the characteristics of the ripple |
|
| 184:30 | . Or you might have some something in mind, but you would have |
|
| 184:34 | sort of parameter to describe the imperfection this mirror. And when that Parameter |
|
| 184:41 | is a perfect mirror and when it's than that, it's more uh it's |
|
| 184:48 | . So you can you can sort imagine modeling this if you had this |
|
| 184:53 | a PhD thesis to analyze this kind stuff, you can imagine that with |
|
| 184:59 | unknown parameter in there. So the the question, the answer to this |
|
| 185:06 | is obviously this is going to depend that parameter, so maybe it's significant |
|
| 185:11 | maybe it's not. So let's keep in mind as we uh go through |
|
| 185:18 | course because we are gonna find cases maybe it's important as a matter of |
|
| 185:28 | , one of them is right So this is real data from my |
|
| 185:34 | days and this is a converted A sea wave split spread gather. |
|
| 185:43 | . Uh this is not a common point gather, but because as we |
|
| 185:47 | about a converted wave has uh image which various as a function of offset |
|
| 186:01 | it's never in the middle. So this is gonna have a split spring |
|
| 186:08 | . And uh let's see here, is this is not a common midpoint |
|
| 186:15 | . It's a common image point gather split with split spread. And I |
|
| 186:24 | you before that because of the uh characteristics of the sea wave reflect a |
|
| 186:34 | coefficient, it should be a anti . So it should be every positive |
|
| 186:40 | here ought to look like a negative over here. So uh it obviously |
|
| 186:46 | , so somebody has multiplied one side the other by a minus one, |
|
| 186:50 | that it looks to be symmetric. okay, that's just uh for |
|
| 186:57 | if you're looking at it with your , now look at this here at |
|
| 187:02 | incidents and zero offset normal incidents, of energy here. So according to |
|
| 187:11 | formula that we just looked at earlier , that's got to be a |
|
| 187:17 | we've got to have zero converted energy normal incidence because as a p wave |
|
| 187:23 | straight down, it can't send a wave back up because it doesn't know |
|
| 187:28 | way the shear wave should be right or left. It's got to |
|
| 187:32 | zero here at this normal incidence, it's clearly not. So one thing |
|
| 187:40 | do is to uh deny the reality what we're looking at. So this |
|
| 187:48 | me of a story um you know you know the story about Galileo and |
|
| 187:56 | was persecuted by the church. He prosecuted by the church lawyers for making |
|
| 188:04 | heretical statement that the earth is not the center of the universe. And |
|
| 188:11 | that was uh obviously a criminal statement he was under house arrest for many |
|
| 188:19 | . I think he died in a in the house arrest. He wasn't |
|
| 188:25 | in prison and a dungeon and he executed. I think she lived out |
|
| 188:32 | final years under house arrest. And uh so while he was being |
|
| 188:44 | he I think he had a judge he didn't have a jury but he |
|
| 188:50 | uh an interrogator. It was called Inquisition. And so he had an |
|
| 188:56 | questioning him about this heretical belief. had the earth was not the center |
|
| 189:02 | the universe. I mean obviously the is at the center of the universe |
|
| 189:07 | God made us and he made the for us to live in. So |
|
| 189:11 | he made us at the center of universe. But here was Galileo saying |
|
| 189:17 | not true. So Galileo had with in the courtroom homemade telescope, he |
|
| 189:26 | a number of telescopes in his Uh And uh I had the privilege |
|
| 189:35 | look through one of them. It it was in uh the italian city |
|
| 189:45 | forenza which in english we call Florence there's lots of very interesting places in |
|
| 189:53 | including cathedrals and museums and one of is the Museum of the history of |
|
| 190:00 | and in that museum there is uh a number of telescopes made by the |
|
| 190:08 | of Galileo and his assistants. And was before he was in house |
|
| 190:14 | And um uh they haven't that the booths a range so that you can |
|
| 190:22 | your eyeball to the viewing piece to eyepiece of the telescope and looked down |
|
| 190:30 | very same look up the very same where Galileo looked hundreds of years ago |
|
| 190:36 | he pointed it at jupiter and he well of course of course. The |
|
| 190:43 | thing he pointed out was the moon found out a lot of interesting things |
|
| 190:47 | the moon. Um while we're talking the moon um do you know why |
|
| 190:59 | moon always presents the same face to Earth? Uh There's always the same |
|
| 191:07 | you look at the moon and there's good clear here of the moon always |
|
| 191:10 | the same. You can see with naked eye, you can see a |
|
| 191:15 | areas and dark areas, you can't much more with your naked eye, |
|
| 191:19 | just with a good pair of binoculars you might use for bird watching if |
|
| 191:24 | look at the moon, you can lots of detail, isn't it? |
|
| 191:32 | that it's because like um it's thicker that side, so the gravity is |
|
| 191:43 | , you're close and so we're gonna to the answer to that question |
|
| 191:47 | But uh it was a question that didn't really know in Galileo's time. |
|
| 191:53 | knew that the moon went around the , but they didn't know why it |
|
| 191:58 | show it's same face to the Now you think well it's it's spinning |
|
| 192:04 | its own axis just like Gareth is . And it must be that the |
|
| 192:08 | of the rate of spin is exactly same as the orbital right. So |
|
| 192:13 | it orbits it spins with exactly the period that shows exactly the same face |
|
| 192:20 | the Earth at all times Now you told us part of the answer, |
|
| 192:26 | talk about more of the answer uh what's your name? So that's one |
|
| 192:33 | the facts that Galileo pointed out is uh the moon in fact does orbit |
|
| 192:40 | Earth, it doesn't slide across the excuse me uh in Galileo's time. |
|
| 192:47 | did not know that the Earth was . No I think they didn't know |
|
| 192:51 | take it back, they didn't know the Earth was round because columbus had |
|
| 192:55 | that uh century before. So um didn't think of the moon as sliding |
|
| 193:01 | the night sky. He thought of moon as rotating around the Earth and |
|
| 193:08 | pointing the uh face of the moon the same direction of the earth. |
|
| 193:13 | he didn't um I didn't know why he could prove that in some detail |
|
| 193:21 | his telescope. Then he pointed his at the next brightest object in the |
|
| 193:26 | which is jupiter and by golly he see it was telescope, the moons |
|
| 193:35 | jupiter orbiting jupiter, They weren't orbiting Earth. So it's you know it's |
|
| 193:42 | in his name that jupiter was orbiting earth but here were some moons orbiting |
|
| 193:48 | which uh definitely established that the Earth not the center of the universe. |
|
| 193:55 | here is Galileo in the courtroom with telescope and the inquisitor and he says |
|
| 194:02 | you know you can just look through telescope and see for yourself that the |
|
| 194:08 | of jupiter orbiting jupiter, uh not Earth so right there that proves that |
|
| 194:14 | Earth is not the uh center of universe. So please declare me innocent |
|
| 194:20 | let me go about my life. that's not what happened. What happened |
|
| 194:25 | the inquisitor reply to Galileo saying I to witness the obscene spectacle of nature |
|
| 194:36 | reason. So he wouldn't look through telescope and perhaps he suspected that if |
|
| 194:42 | did a doubt might call into his about the Earth being uh the center |
|
| 194:50 | the universe. So in order to that doubt out of his mind, |
|
| 194:54 | refused to acquire the data. He to look through the telescope. Well |
|
| 195:02 | right there you see he had a and Galileo was saying well here's some |
|
| 195:10 | to check your theory. And he denied he was refusing to look at |
|
| 195:14 | data because he liked his theory and wanted to keep his theory. Now |
|
| 195:20 | that discussion about the moon back to figure that you're looking at here. |
|
| 195:27 | have theory that says that the amplitudes at zero offset should be zero should |
|
| 195:36 | known that you can see there's lots amplitude here. So we can either |
|
| 195:41 | what the inquisitor did and deny the to keep our theory intact or we |
|
| 195:48 | say there must be something wrong with theory. That's the scientific group. |
|
| 195:56 | must be something wrong with the theory the data always has primacy over the |
|
| 196:04 | . Now, the data could be . Somebody might have screwed up here |
|
| 196:08 | the data could be wrong. But know, we can investigate that and |
|
| 196:13 | have and this kind of data is uh it says it's common. It's |
|
| 196:21 | It occurs in cases like 10% or of the cases where you look at |
|
| 196:27 | uh it's not very common, but not very rare either. And it's |
|
| 196:35 | at odds with the theory. The definitely says we should have zero. |
|
| 196:42 | what could be causing these uh finite at normal incidents? So one explanation |
|
| 196:51 | imperfect reflections. So this energy is not from the expected reflection point, |
|
| 196:59 | from the funnel zone uh surrounding the reflection point. Maybe for these uh |
|
| 197:07 | and most layers are like that. see uh right in here, there's |
|
| 197:15 | uh that's a reflection event which is small and normal. So maybe this |
|
| 197:21 | doesn't have an imperfect mirror, but of these do have imperfect reflected. |
|
| 197:29 | you see what we needed to um we needed to have, we need |
|
| 197:37 | have this kind of data to see if this if this had been p |
|
| 197:42 | data with the same kind of imperfect down there, we would interpret these |
|
| 197:49 | that complication and we would interpret it by adjusting our the parameter delta Z |
|
| 197:56 | Z. But since we, the says this should be a hard |
|
| 198:02 | we are forced to to the conclusion our theory that we spent so much |
|
| 198:08 | and effort developing In the past two . Uh That's wrong somehow. That's |
|
| 198:16 | we made an approximation which we And this is a very good, |
|
| 198:22 | very good way to say, we need to go back and uh |
|
| 198:27 | what happens in imperfect reflectors. And we can see already intuitively that if |
|
| 198:33 | if the reflector is imperfect, then gonna have uh non zero conversion at |
|
| 198:42 | incidence anyway. And the strength of are going to depend upon the amount |
|
| 198:46 | imperfections. And we can we now a more elaborate theory with another unknown |
|
| 198:53 | in there, which is, you , the the imperfections in the theory |
|
| 198:57 | the imperfections in the mirror and we adjust that unknown parameter to match this |
|
| 199:03 | . But there's there is a problem problem that this explanation is implying that |
|
| 199:10 | all of these reflection events has that of imperfection all the way down. |
|
| 199:16 | maybe that's a bit of a you would think that uh if that |
|
| 199:20 | happening uh if it happens at all here would be very common in our |
|
| 199:27 | instead of partly common in our So I would say that most converted |
|
| 199:32 | data sets don't look like this. of them have zero or very minimal |
|
| 199:37 | here, normal lawsuits and this one uh any of them. So this |
|
| 199:45 | be part of the answer, but not convinced that's the whole answer. |
|
| 199:49 | I would say that our community of geophysicist has not uh coped with this |
|
| 199:58 | . Who really cares? I mean of the data we look at 99% |
|
| 200:02 | our data is not converted wave So do we really care about |
|
| 200:10 | Or is this just uh an academic here? Well let's think about |
|
| 200:19 | If um uh if these reflections are and if we're gonna have significant energy |
|
| 200:29 | from everywhere in the funnel zone, that gonna affect our ideas about Avio |
|
| 200:36 | we um we developed a B. . For p ways assuming perfect |
|
| 200:43 | But if they're not perfect, doesn't mean that our our Avio analysis is |
|
| 200:50 | ? Of course it does. Because know this additional convert a way of |
|
| 200:55 | that you can see right here. got to come from the other |
|
| 201:00 | We've got to have conversion of uh energy between the incoming and the outgoing |
|
| 201:06 | , all the energy has to add the same. Otherwise the reflective boundaries |
|
| 201:12 | gonna get hot down there. They get hot down there. So the |
|
| 201:17 | energy that you can see with your right here has got to come from |
|
| 201:22 | other outgoing waves and it would be miracle if none of this excess convertir |
|
| 201:28 | of energy came from reflected p It's just almost I worked through the |
|
| 201:35 | completely. But even even in the but I can think automatically it must |
|
| 201:43 | would be amazing if none of this energy here came at the expense of |
|
| 201:48 | reflected P wave which is our primary source and exploration. So this is |
|
| 201:54 | really important result that shows that are about the reflection process which is universal |
|
| 202:02 | our business is maybe oversimplified in a way. So solving this problem is |
|
| 202:10 | solve is gonna have big implications about leo analysis and it's another great um |
|
| 202:20 | for PhD thesis. So we have a few minutes late here. Uh |
|
| 202:30 | talk talk our way through all these it here in the bottom and since |
|
| 202:34 | of the above so be alert to . Which of these statements is |
|
| 202:37 | Go on. A in the That is unrealistic to believe that seismic |
|
| 202:42 | are perfect in our elastic discontinuities. true because the results are the results |
|
| 202:48 | a sedimentary process. Nobody has been there making a perfect plane. So |
|
| 202:55 | course that's true. Go on. actually every point on a reflector. |
|
| 203:00 | energy in all directions. Not just the angle of incidence. True, |
|
| 203:06 | true, go on. So we two that are true. So we're |
|
| 203:09 | for easy but we got to verify C and D. Are also going |
|
| 203:13 | see those distractions from within the first zone arrive at each receiver only slightly |
|
| 203:19 | . Yes. Okay but you you the name of monsieur. So don't |
|
| 203:25 | that s okay for now otherwise people think poorly of you. Just like |
|
| 203:32 | you pronounce the word if you say poison. Uh people will think badly |
|
| 203:38 | so I don't want your your your if people think badly of you they're |
|
| 203:46 | be badly of of the geology department U. Of H. So you |
|
| 203:53 | know gotta know how to pronounce croissant you have to know how to pronounce |
|
| 203:58 | . Go on to D. They received amplitudes to a degree that depends |
|
| 204:04 | the imperfections in the reflector. That's . Yeah so we got E. |
|
| 204:08 | all of the above good. Okay that brings us to the end of |
|
| 204:11 | and we'll take up on next um next friday at 1 30 Pick up |
|
| 204:21 | uh at this point. So now uh let's talk a little bit uh |
|
| 204:26 | that okay to start at 1 30 friday? Okay um Should we be |
|
| 204:33 | in person or uh remote? I'm with friday being in person. Just |
|
| 204:41 | my job is like not even 20 from the U. Of H. |
|
| 204:47 | so so let's let's do that. uh let's meet at room 2 13 |
|
| 204:55 | Friday. And then we'll play it ear for Saturday just like we did |
|
| 205:01 | . I think the rains are gonna still with us right next Saturday. |
|
| 205:05 | not sure anyway, so that's So and we'll take up some next |
|
| 205:10 | at 1:30 on campus at this so I'm gonna stop sharing. |
|