| 00:00 | is everybody seeing this now. So since the recording is in progress |
|
| 00:07 | , let me back up just a . And uh let's say first, |
|
| 00:11 | get rid of this. So this where we started. And uh this |
|
| 00:15 | where we left off yesterday, starting the discussion of two waves. Uh |
|
| 00:24 | I have it'll be okay, but lost my mouse. So uh two |
|
| 00:31 | are different because the surface in question in a bar hall is cylindrical, |
|
| 00:37 | flat. And of course it's not cylindrical, but it's uh it's close |
|
| 00:42 | to cylindrical that it makes sense to it in cylindrical coordinates, uh rather |
|
| 00:50 | Cartesian coordinates. And so we see um uh surface waves traveling up and |
|
| 00:59 | the bar hall, localized near the of the bar hall. We see |
|
| 01:04 | in all DSPs. And I'll just you of ES. P as a |
|
| 01:07 | seismic profile wherein the sources are at surface and the receivers are down |
|
| 01:14 | And of course we also see them sonic logs. And so uh there |
|
| 01:19 | many types of course, uh and they're called tube waves for obvious |
|
| 01:25 | And uh so now these are not we want to analyze in sonic tools |
|
| 01:36 | when you have a sonic tool in bar hall, you know, maybe |
|
| 01:41 | or break the Hughes or somebody has uh slowly the service and they're doing |
|
| 01:48 | of our companies don't have the capability do these kinds of logs ourselves. |
|
| 01:54 | we just pay one of the service do it. So, uh well |
|
| 02:06 | tool measures is not a tube wave it measures a body wave critically |
|
| 02:13 | And so we will learn more about that means in less than seven. |
|
| 02:21 | , so they all propagate in one . A polar down hall were both |
|
| 02:26 | they are analyzed using a cylindrical coordinate for obvious reasons. They decay exponentially |
|
| 02:33 | from the borehole wall into the formation also back into the mud. Because |
|
| 02:42 | have in any two boys problem, have uh the diameter of the bore |
|
| 02:50 | , the diameter of the cylindrical Uh that that's always going to get |
|
| 02:57 | our equations, we know that. so that is gonna lead to frequency |
|
| 03:02 | behavior because that borehole diameter provides um standard by which any particular frequency knows |
|
| 03:12 | it's high frequency or low frequency dependent whether its wavelength is greater than the |
|
| 03:20 | time. And as they're going up down, they reflect from every formation |
|
| 03:28 | . So let's just assume the mud continuous up and down the hall. |
|
| 03:33 | uh wherever there's a formation boundary and , which which was penetrated by the |
|
| 03:42 | that's the boundary and it reflects. if it's going up, those reflects |
|
| 03:47 | down and somehow transmitted and so And then here's something else you might |
|
| 03:51 | have thought of if we're doing this casing wherever there's a casing joint at |
|
| 03:58 | point, there's a double thickness of . And so it reflects off of |
|
| 04:03 | . And also um you know the itself is occupying the middle part of |
|
| 04:10 | borehole. And it's got a wire coming out the top but then it's |
|
| 04:15 | some sort of tool down in the and uh uh there's gonna be uh |
|
| 04:23 | changes in the two way behavior because changes in the tool diamond, maybe |
|
| 04:32 | the tool itself is maybe six inches and then the wire line is maybe |
|
| 04:39 | inch across. So right there there's diameter change in the tool which is |
|
| 04:45 | to affect the two waves going out and down. You can think that |
|
| 04:50 | it's propagating the partner which is in in the mud, it's going to |
|
| 04:55 | affected by whether or not there's a um right there so you can see |
|
| 05:01 | being pretty complicated. Yeah. Um most important to tube wave is a |
|
| 05:08 | called Stoneleigh wave because the only uh it but it should be called the |
|
| 05:16 | wave since it's like the Sheltie wave we talked about yesterday, remember the |
|
| 05:22 | wave is like, it's the only except that the upper medium is um |
|
| 05:28 | instead of air. And so that's situation in the borehole. So now |
|
| 05:33 | got a picture of half of the hall here. This is I'm going |
|
| 05:36 | assume the borehole is symmetrical and you see half the tool here and half |
|
| 05:42 | wire line here, pulling it up tube and it's being pulled up by |
|
| 05:47 | . Um Normally what they do is let it settle down to the |
|
| 05:51 | under some weight and then they pull up slowly and steadily. And uh |
|
| 05:56 | here is uh Uh two lens and wire line begins. So obviously the |
|
| 06:04 | wave is going to propagate differently up than it is here. And so |
|
| 06:08 | the cartoon you can see a bunch layering that's quite now an important |
|
| 06:18 | Mathematical complication comes from cylindrical geometry. let's just turn the geometry around so |
|
| 06:25 | looks like a layered halfway, a rarely way problem on a cylinder. |
|
| 06:30 | this looks pretty much like what the cartoon we started off with yesterday |
|
| 06:36 | a formation here. Never mind It's anti psychotropic and layered down |
|
| 06:40 | That in our simple analysis, we're going to consider that at all. |
|
| 06:45 | remember this is not flat. Like talked about, this is a cross |
|
| 06:50 | of roof. So I said that's our corner system is gonna look |
|
| 06:57 | It's gonna have uh actual coordinate and gonna have a radio coordinate and an |
|
| 07:05 | azimuth to the to the more whole . So we're gonna ignore the presence |
|
| 07:12 | the tool. And also the like so we're gonna look uh in |
|
| 07:17 | solutions like this. Remember when we the rarely way uh different really wave |
|
| 07:27 | love waves is really wave has displacement the plain of the figure. And |
|
| 07:32 | what we're gonna be looking at here way will be polarized in the |
|
| 07:42 | Z. Plane. Okay, so is a big difference in the |
|
| 07:48 | Uh In fact, we're gonna use we're gonna do very much like we |
|
| 07:54 | yesterday in the wave equation appears the . Um And so the application looks |
|
| 07:59 | this in a cylindrical coordinates. See part looks like a Cartesian part and |
|
| 08:07 | part looks like a shark apart. uh that's the whole thing looks |
|
| 08:13 | you know, driving that dishes outside scope of this course. You can |
|
| 08:22 | up in any in any book on physics. This definition awesome operator in |
|
| 08:34 | . And uh remind you here that this is uh in the two |
|
| 08:39 | Case there's no as mental dependence here we're going to look at waves which |
|
| 08:47 | independent as. So here's our it's wave equation on the left. Uh |
|
| 08:58 | this is gonna be further in the . And so here we're gonna have |
|
| 09:03 | p waves of parts in the fluid here's the the time derivative. And |
|
| 09:08 | is the space derivative. And uh gonna give uh rotation uh k overall |
|
| 09:20 | the fluid. We're gonna call decent of course uh had a body wave |
|
| 09:27 | through the fluid. It would be with that philosophy, but rarely waves |
|
| 09:32 | me the Stoneleigh wave in this uh tube wave is not gonna travel with |
|
| 09:38 | own philosophy, not this velocity. , so uh we're gonna we're gonna |
|
| 09:44 | the solution. So uh suppose that all are not uh a little bit |
|
| 09:53 | by this notation. So let me tell you what it is that by |
|
| 09:59 | zero, in the case of that standard notation, for what they |
|
| 10:04 | mathematician called a modified vessel function of zero. Okay, now, um |
|
| 10:12 | correspond to uh and uh we're doing flat problem with Cartesian coordinates. These |
|
| 10:23 | correspond to signs and Cozzens, but and Cozzens don't really work in the |
|
| 10:30 | geometry. So we have to use basis functions. Um They call modified |
|
| 10:38 | function. So, vessel was one these mathematicians in the 19th century and |
|
| 10:44 | are modified in a way to be . I don't know what, how |
|
| 10:49 | modified, but you can look them in a handbook, just like you |
|
| 10:52 | look up science and frozen. So your mind, you should think of |
|
| 10:57 | like science and cosign and uh tabulated . You can look them up and |
|
| 11:05 | functions of a non dimensional variable. the non dimensional variable uh or it |
|
| 11:12 | that uh that here we have a um coefficients and we're going to determine |
|
| 11:21 | from the boundary condition. Uh just much like we did yesterday. And |
|
| 11:28 | so uh you can see here uh have the radius and we have the |
|
| 11:36 | along along the bar. Oh by way, you can see from the |
|
| 11:39 | of this exponential functions that it's wiggling way along the borrow. It does |
|
| 11:45 | travel in any direction but in the of the world. And it's got |
|
| 11:52 | a wave number, component Gsfc. here's the radio component of that same |
|
| 11:58 | number. So uh same that same vector, so the length of the |
|
| 12:05 | square of the length of the victors by the pythagorean there, just like |
|
| 12:10 | um yesterday and that's related to the velocity, just like we did |
|
| 12:19 | And so uh so you can see G. Is a function of of |
|
| 12:25 | . So here uh with every omega gonna be a different uh G. |
|
| 12:32 | um here and here and so together are gonna make up, we're gonna |
|
| 12:38 | able to add together uh spectrum a like this to find the answer for |
|
| 12:47 | problem. Even the most complicated. , so now we're looking in the |
|
| 12:56 | as with the railing wives, the is neither curl free nor divergence free |
|
| 13:02 | of the boundary conditions, which we go over again. I don't think |
|
| 13:07 | we just mentioned curl free part will the wave equation for the scale of |
|
| 13:12 | . And I see this has this the scale of potential for the rock |
|
| 13:18 | up here. This is the scale potential. Uh And then it's gonna |
|
| 13:23 | a divergence free part which will obey wave equation for the effective potential in |
|
| 13:29 | rock. And so this has got rock p wave velocity here and a |
|
| 13:36 | shear wave velocity here. So you to see how this is all very |
|
| 13:43 | again. I want to think for to think of these as elastic |
|
| 13:47 | Wave is going to travel with the wind velocity. Now. Uh we're |
|
| 13:57 | uh you gonna uh say that uh we did before, we can uh |
|
| 14:06 | when we were doing the stone, flat Stoneleigh problem yesterday we decided that |
|
| 14:11 | only needed the transverse component of this . We called it side to its |
|
| 14:17 | to uh the other two vectors. In this case that transverse vector is |
|
| 14:24 | call that transverse component is gonna be side signify 20 in the so um |
|
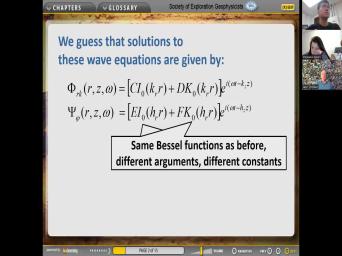
| 14:38 | So we're gonna do like we did , we're gonna guess the solution and |
|
| 14:42 | the guests. So uh careful for potential for the scalar potential in the |
|
| 14:51 | . We got the same two best vessel function with different arguments. So |
|
| 14:56 | is the uh radio component of the way vector. And here is the |
|
| 15:03 | component. This is traveling in like before in the Z. Direction |
|
| 15:09 | It's got different constants and uh And otherwise it's just like what we |
|
| 15:17 | at before, in the foot for uh Thank you. Like component vector |
|
| 15:27 | . It's similar same to a vessel , modified vessel function with non dimensional |
|
| 15:36 | given by the radius and rate of part of the h. Each wave |
|
| 15:46 | here is the two more constants. see this is getting complicated. Um |
|
| 15:58 | are not gonna follow through this analysis the detail we did yesterday. Um |
|
| 16:09 | these uh these these these guesses will the wave equation. If the wave |
|
| 16:16 | have the length, the length of K. Wave vector is going to |
|
| 16:19 | related to the the velocity, wave velocity and rock. And the |
|
| 16:26 | of each wave vector is very similar for the sure loss. All these |
|
| 16:35 | together we uh all three of these wave vectors have to have the same |
|
| 16:42 | axel component. And it's gonna be pleasure minus omega over the Stoneleigh way |
|
| 16:48 | Alaska, christian wonder what we did . Boundary conditions are continuity of stress |
|
| 16:55 | displacement of the borehole, daughter, stress and displacement on the actors. |
|
| 17:05 | along the actors. We cannot have infinite stress uh at the action. |
|
| 17:13 | gotta go smoothly to uh some finite . And then uh as uh as |
|
| 17:22 | the wave continues to the other half the bar hall past the actress, |
|
| 17:28 | will change again and again reach the condition at the other side. Now |
|
| 17:39 | way out into the uh into the Uh the stress and displacement has to |
|
| 17:47 | to zero. We didn't say that for the flat problems that we did |
|
| 18:03 | . I don't think that's required. flat problems certainly didn't use it. |
|
| 18:11 | that will be important here because of 600%. Now suppose you had a |
|
| 18:20 | . Uh then that complicates things. there's yet another set of solutions for |
|
| 18:26 | let's enter equations for inside the tool . And so normally when people do |
|
| 18:32 | , they do not attempt to find solution for a real tool is too |
|
| 18:37 | . So they assume uh at this in the analysis, they assume the |
|
| 18:44 | is a solid uh solid uniform solid any machinery inside the tool. And |
|
| 18:53 | has a radius, they know the of the tool. And uh so |
|
| 19:00 | makes a complication. As you can maybe a significant country complications as we're |
|
| 19:06 | going to deal with that. So you uh when you do this um |
|
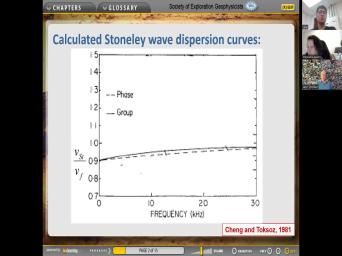
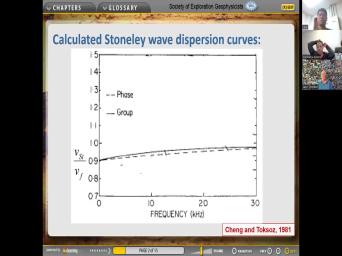
| 19:13 | this is the kind of answer you . So here is the Stoneleigh wave |
|
| 19:17 | a as a fraction as a ratio washing in the floor as a function |
|
| 19:26 | frequency for a given um for a instance of course. And um you |
|
| 19:37 | see here we have the phase velocity calculated for that model like this and |
|
| 19:44 | group velocity is calculated like this. this is uh citing paper by Cheng |
|
| 19:50 | Tacos 1981. So um pretty old 40 years old. So let me |
|
| 19:56 | tell you uh such uh interesting fact these uh Tacos was a professor at |
|
| 20:05 | . I. T. Which is in massachusetts. And Uh it was |
|
| 20:11 | very prominent your physicist now retired still by the way. Um and the |
|
| 20:17 | he's alive is because he married a wife about 10 years And he was |
|
| 20:25 | famous professor at M. IT for years. I think he retired about |
|
| 20:30 | years is a bit older than me so he may be retired 15. |
|
| 20:39 | um so um Chin was I think was a student and he was such |
|
| 20:47 | good student that he became his associate M. I. T. And |
|
| 20:52 | ran a consortium at M. Eight . I. T. For many |
|
| 20:56 | now Cheng was just elected president of S. E. G. Uh |
|
| 21:02 | month. So that's interesting. Uh assistant surpassed the master. So in |
|
| 21:10 | days checking and was the boss and was the subordinate. But when Cocteau's |
|
| 21:18 | he had never been president of the . But um but Cheng just was |
|
| 21:25 | president of the S. And Uh last a month ago. And |
|
| 21:33 | by the way he is the editor the journal Geophysics. I don't remember |
|
| 21:40 | another time when we had one guy was the president elect of the society |
|
| 21:50 | the editor at the same time. the way the scG works is we |
|
| 21:54 | a president elect and he's sort of the vice president except there's also a |
|
| 21:59 | president, but he's gonna inherit the automatically next year unless he works to |
|
| 22:06 | something unethical or so something like I don't think that's gonna happen. |
|
| 22:12 | he's gonna uh 99.9% probability he will the president of the ScG next year |
|
| 22:22 | he will be the first chinese president the ScG. Very interesting. And |
|
| 22:29 | have lots of members of course in . And of course we have um |
|
| 22:34 | of chinese geophysicists in this country and in europe. And uh and we |
|
| 22:41 | lots of chinese students in this So um let me just interrupt |
|
| 22:48 | Mr wu are you a member of S. E. G. Yeah |
|
| 22:54 | you've got to be both of, have to be members of the professional |
|
| 22:59 | . And I encourage you to also members of the local affiliate society, |
|
| 23:05 | Geophysical Society of Houston. And uh encourage you both to participate actively in |
|
| 23:14 | local society and to what extent is in the international society as. So |
|
| 23:21 | will be good for you. Professional it. Okay so uh Cheng uh |
|
| 23:29 | when they did this 40 years ago they were both living in Boston. |
|
| 23:34 | and I should I should tell you taxes retired, uh they needed somebody |
|
| 23:40 | to run the consortium. The consortium called Earth Resources Laboratory. And had |
|
| 23:49 | know about About six or 10 students it had maybe a couple of |
|
| 23:56 | And the major professor was Texas. after Tacos retired, they appointed some |
|
| 24:05 | professor to one of the uh to the consortium. And um then I |
|
| 24:12 | he retired and uh made an unconventional uh to be an interim director of |
|
| 24:23 | consortium while they were searching for a director. And the the interim director |
|
| 24:29 | the former executive director that is they paid um She was a high level |
|
| 24:38 | person and then she took care of day to day running of the consortium |
|
| 24:43 | the director is uh being a And so they asked her then to |
|
| 24:50 | the acting director of the consortium, she did very capably for about a |
|
| 24:56 | or two while they did a search a new director. And then once |
|
| 25:01 | new director came on board, she resigned of course as director of the |
|
| 25:10 | . But she did such an outstanding in that role that she was elected |
|
| 25:15 | years ago to be the president elected . And she is now the current |
|
| 25:21 | of ScG. Actually, she was until thursday last thursday, her term |
|
| 25:27 | . And um so she is now president Sug and it doesn't mean that |
|
| 25:37 | is free of all ties to E. G. There is a |
|
| 25:43 | sequence of important roles that she has perform for the S. E. |
|
| 25:50 | . For the next five years like of important committees. So she she's |
|
| 25:56 | I think she's sitting now today on nominations committee for the S. |
|
| 26:01 | G. And in a few years will be the chair of nominations. |
|
| 26:06 | also I think she's sitting on the and awards committee in a few |
|
| 26:10 | she will be the chair of that uh because she is a former president |
|
| 26:19 | several years of declining important responsibilities for president. So that means that um |
|
| 26:31 | have two recent um graduates, two uh insertion. Uh My g who |
|
| 26:43 | now leading this society, her name ANna Shaughnessy and his name is Arthur |
|
| 26:50 | both excellent cheer physicist. And uh step down from that role on thursday |
|
| 26:59 | do is on the last day of convention, they meet at noontime and |
|
| 27:06 | officially hand over the responsibilities from the president. Uh and the old executive |
|
| 27:14 | . And the old board gets handed to the new people who have been |
|
| 27:19 | elected throughout the summer. And so I think we have we always have |
|
| 27:26 | , well it's not complete turnout, people who continue in their previous roles |
|
| 27:33 | then some uh turn over their roles really elected people. So that all |
|
| 27:39 | on thursday at lunchtime while we were lunch, they were doing this |
|
| 27:46 | And then uh the old uh administration and has a drink in the uh |
|
| 27:55 | the bar and congratulate themselves for having a good job. And then the |
|
| 28:01 | board has a short business meeting and they uh german and then they have |
|
| 28:08 | serious business meeting, I think this , this coming week we're going to |
|
| 28:13 | it and then monthly thereafter. So the way the sug as your work |
|
| 28:19 | the way. But when I was scG president, we didn't have a |
|
| 28:24 | of directors. All we had is meeting five people, you know, |
|
| 28:30 | , vice president. And so we that that was not good, That's |
|
| 28:37 | an appropriate governance structure. So we uh that was 19, no, |
|
| 28:45 | was the year 2006 I became And during that year we launched a |
|
| 28:55 | for reforming the uh sug governance. and it took several years for that |
|
| 29:01 | mature because you have to decide what want to do is to educate the |
|
| 29:08 | and then you have to have a for the membership. And then, |
|
| 29:12 | know, it takes a while, what we did. And the new |
|
| 29:17 | started happening, I think about 1000 mine. That's so we've been running |
|
| 29:24 | that pretty well. Uh there's some exceptions pretty well ever since. And |
|
| 29:34 | the new board, you set of has just taken office and uh in |
|
| 29:43 | business very shortly. Okay, so to science. Uh here we have |
|
| 29:49 | phase and group velocities. And you we talked yesterday about how those different |
|
| 29:58 | each other. And I think it's common that those two velocities are similar |
|
| 30:04 | not identical. And you see the way velocity is a little bit less |
|
| 30:10 | the mud velocity. And uh look here at zero frequency. Uh the |
|
| 30:19 | and group velocities are the same And also at various type treatments, they're |
|
| 30:25 | same and in between they're not the . So look at the band we're |
|
| 30:29 | about this is Kilohertz. So these are too high for seismic waves if |
|
| 30:36 | launch a wave like this, uh 10 kHz from uh surface source. |
|
| 30:46 | wouldn't go very far because of Um um in the earth. Remember |
|
| 30:53 | told you, I think I told that insinuation you can think of is |
|
| 30:58 | constant in terms of of energy loss site. And so high frequency waves |
|
| 31:08 | more cycles per meter than the low waves. So these high frequency waves |
|
| 31:13 | many cycles before they get down into uh more than a meter or |
|
| 31:18 | So they just die up. of course, um A source like |
|
| 31:24 | think about a source like dynamite impulsive that generates all all frequencies including these |
|
| 31:32 | these high frequencies. Most of them out. And so the only ones |
|
| 31:36 | propagate down thousands of feet and come thousands of feet to our reporters. |
|
| 31:42 | are lower frequencies in the seismic say between five hertz and 100. |
|
| 31:50 | it's uh 100 times 1000. it's 100 times less than wave theory |
|
| 32:03 | wave theory. And uh everything uh analysis comes through regardless. Now there's |
|
| 32:13 | um kind of mhm Really wait, another kind of tube ways which is |
|
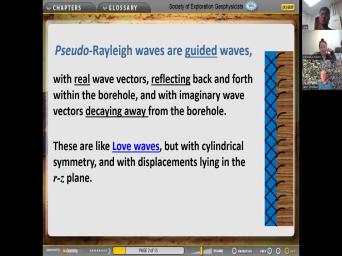
| 32:22 | of like love ways and these are pseudo railing ways. Um and so |
|
| 32:28 | have real vectors, just just like the love problem that we had you |
|
| 32:32 | here uh wavefront echoing back and forth the fluid. Uh And uh in |
|
| 32:40 | solid you can see exponential decay. these have um or stir they're uh |
|
| 32:50 | not propagating in in here with as here is a ray as array and |
|
| 33:01 | can be certain that in the mud uh it's polarized in this direction, |
|
| 33:10 | not polarized, transverse. Like uh it's uh in this direction, but |
|
| 33:16 | it's bouncing back and forth at an in the in the mud. And |
|
| 33:28 | uh similar in lots of ways to love waves which we so this is |
|
| 33:37 | same diagram as we saw before except you see right here there's just covered |
|
| 33:48 | covered up stuff in the this figure a white panel. So you wouldn't |
|
| 33:53 | distracted. And now you see there is the whole thing. And so |
|
| 33:59 | is what we looked at before. then the pseudo really waves are um |
|
| 34:05 | have different branches here. And you see for frequencies, her frequency is |
|
| 34:13 | about changing the hearts in this The pseudo really wave doesn't propagate at |
|
| 34:21 | . And for uh uh huh good uh as a velocity which decreases with |
|
| 34:33 | rapidly and then look, it turns and increases again. So whenever you |
|
| 34:41 | uh you know, dispersion curve like , whenever you see a case where |
|
| 34:52 | locally independent or frequency turns around and back up, uh that's gonna mean |
|
| 35:01 | a lot of energy is going to concentrated in this frequency band in the |
|
| 35:06 | . And this was first discovered by guy named Harry. So here is |
|
| 35:13 | synthetic size program that shows all these . So, let's look and see |
|
| 35:17 | we have here is the p wave we didn't talk about but we will |
|
| 35:24 | about that um seven very low, low amplitude here is the shear wave |
|
| 35:33 | by the way, there's very stuff here which uh these are the pseudo |
|
| 35:40 | railways, which we just mentioned, you can see uh growing in um |
|
| 35:45 | amplitude. The uh the later ones growing inactive and you can see and |
|
| 35:54 | see that this is a little bit frequency and this is a little bit |
|
| 35:59 | frequency here, and the stony waves then following along behind. Just like |
|
| 36:12 | just like I said here, the waves are gonna be slower and most |
|
| 36:16 | the time most. And the the where the maximum and uh that's a |
|
| 36:29 | that's called the area maximum. And is happening um with these frequencies and |
|
| 36:36 | exactly the same frequencies as you saw the previous slime because it's the same |
|
| 36:44 | . Yeah, that's a very idealized . I would say that I call |
|
| 36:49 | difficult, but not impossible if you motivated, you could work your way |
|
| 36:59 | that um yourself, I think this Arthur Cheng's PhD thesis Watson. Uh |
|
| 37:07 | in those days it was pretty advanced . Um but you could probably work |
|
| 37:12 | way through it uh if you were , but then we got to recognize |
|
| 37:21 | in the real case uh Warhol is gonna be cylindrical. Uh And |
|
| 37:29 | it might not be vertical, it be d created towards the horizontal direction |
|
| 37:34 | maybe even uh in the horizontal and it uh So that's assuming the layers |
|
| 37:42 | all horizontal. For now it will a encounter. The borehole wall is |
|
| 37:48 | be uh nice entropic because of that . And that's gonna make it |
|
| 37:56 | Furthermore. Think about this. Think the problem that we had in the |
|
| 38:04 | , which we talked about his first with a simple sedimentary, simple sedimentary |
|
| 38:16 | , which is uh sitting in a field science saluted by gravity and stress |
|
| 38:23 | the uh scratching all the way down the vertical stress is going to be |
|
| 38:31 | than the horizontal stress as we talked in the real world, uh we're |
|
| 38:36 | have in that uh sedimentary sequence, gonna have a borehole. So it's |
|
| 38:43 | gets into her job analyzing stress She's gonna have she's gonna be dealing |
|
| 38:51 | uh data taken down home. And as soon as you introduce a more |
|
| 38:59 | into a stressed solid that affects the , you know, that introduces a |
|
| 39:05 | surface inside this stress solid where the shear stresses vanish at that cylindrical uh |
|
| 39:18 | cylindrical surface. So what that does it concentrates, it changes the distribution |
|
| 39:25 | simply because of the fact that you in there, a stress free |
|
| 39:30 | And suppose it's not um exactly Suppose it's uh as opposed to as |
|
| 39:39 | bit shoot its way through the through the rock, perhaps it didn't |
|
| 39:50 | a perfectly cylindrical. Okay. And suppose that the uh initially not only |
|
| 40:02 | manmade complications, but suppose that the stresses are not equal in this |
|
| 40:09 | So all of those factors mean that this redistribution of stress caused by the |
|
| 40:17 | hall can be complicated. And in it concentrates, concentrates some of the |
|
| 40:24 | of stress near the bar hall In some cases those complicated stresses change |
|
| 40:34 | shape of the bar hall. Uh called borehole breakouts and pieces of |
|
| 40:43 | of the borehole break off and fall the borehole because of this stress concentration |
|
| 40:51 | you know, depending on the rock ? So some rocks are strong and |
|
| 40:55 | doesn't happen, other rocks are weak it is come have pieces of the |
|
| 41:03 | the formation right there, four whole break off and fall into the |
|
| 41:10 | And normally uh they get extracted as are happening, you know, uh |
|
| 41:16 | are being uh pulled out and removed and the whole bit is being replaced |
|
| 41:25 | so on. So normally what happens those things get disposed of? So |
|
| 41:30 | don't really have pieces of rock in borehole. But um over there and |
|
| 41:39 | so so Stephanie's doing her borehole She should be alert to maybe the |
|
| 41:49 | that maybe the two horizontal stresses in borehole are not the same. |
|
| 41:55 | we uh we detect these bar hall . There's a tool which is called |
|
| 42:06 | caliper tool, that's what it's it goes down uh measures the shape |
|
| 42:12 | the bar hall as it goes And as it passes one of these |
|
| 42:16 | , it notices that for a whole inner is different in one direction than |
|
| 42:22 | another direction. So that's part of caliper law. And so Yeah, |
|
| 42:30 | been in business a long time since 1930s and has dozens and dozens of |
|
| 42:36 | measurements that they can sell to Uh So the service of course. |
|
| 42:43 | um one of those is caliber tool it's run fairly frequently so that you |
|
| 42:49 | blindly assume you know what question. . Um Is this also because we |
|
| 42:59 | this one test at work it's called miniature vein. Um I'm not sure |
|
| 43:05 | you're familiar with it. Would this kind of related to that? Cause |
|
| 43:09 | it's called like a soil saber? we um we only do it with |
|
| 43:14 | tube samples. Um and we have put the saber in and turn it |
|
| 43:19 | it measures the the sheer failure um the in the moment of failure for |
|
| 43:26 | only do it for clay and we got like this huge job in for |
|
| 43:31 | a pipeline. And yeah we just this it's a soil saber that measures |
|
| 43:38 | shear stress of when it fails. have to do remolded and then like |
|
| 43:43 | received. So I don't know if am not familiar with that. No |
|
| 43:48 | think it's really interesting. Uh So should familiarize yourself in a serious way |
|
| 43:54 | it and uh and also familiarize yourself the assumptions that you make when you |
|
| 44:03 | the data that you're gonna come back . Some kind of a data. |
|
| 44:07 | I'm not sure what it's gonna look but uh it's not what the customer |
|
| 44:11 | . You want that data to be in some way and you should make |
|
| 44:16 | that you understand what assumptions your company making as it does that interpretation. |
|
| 44:24 | so I'm not familiar you know uh testing companies have are been around for |
|
| 44:34 | long time but they're constantly thinking about they can do differently to uh help |
|
| 44:42 | customers and the customer standing at the of the bar hall looking down and |
|
| 44:47 | what's down there. And so uh like yours help them understand better what's |
|
| 44:54 | there. And it can be important a lot of reasons and I am |
|
| 45:00 | familiar with that particular. Okay, here's another real world issue. I |
|
| 45:11 | told you about one type of drilling , borehole breakouts. Another type is |
|
| 45:16 | we call mud cake. So as uh the driller is drilling, he's |
|
| 45:23 | in the bar whole um uh borehole . And he can adjust the density |
|
| 45:30 | that mud by adding or extracting solid at the top and circulating it |
|
| 45:38 | And so he likes to maintain. inside the bar hall it's easy to |
|
| 45:44 | the pressure inside the Warhol, it's that uh integration of all the pressure |
|
| 45:53 | to the density of the mud all way up to the surface. And |
|
| 45:59 | so he likes to maintain the pressure the bar hall at all depths to |
|
| 46:07 | a little bit higher than the natural fluid pressure in the formation as he's |
|
| 46:15 | because he doesn't want the formation starts come into the bar. He wants |
|
| 46:20 | while he's drilling. And so he he adds enough solids to the mud |
|
| 46:27 | make sure the pressure at all depths the hole a little bit higher and |
|
| 46:33 | formation pressure. What that means is he's going to be losing more whole |
|
| 46:40 | into the formation because the pressure is in the mud in the borehole. |
|
| 46:46 | the formation fluids as the formation mud into the surrounding formations. The ferocity |
|
| 46:57 | a tendency to filter out the particles the mud. So clogs up the |
|
| 47:03 | in the formation, gets clogged up blood particles. And the uh the |
|
| 47:10 | is happy with that because what that is the club, uh blood particles |
|
| 47:16 | in the uh in the formation in the outer inch or so of |
|
| 47:21 | formation wall are gonna reduce the So he loses less mud in the |
|
| 47:27 | as it progressively chokes up the ferocity silent particles from the mud. And |
|
| 47:35 | that uh that um cylindrical um interval formation just outside the uh Warhol which |
|
| 47:51 | clogged with mud particles, we call mud cake but jake. And so |
|
| 48:00 | in the two great problems that we talked about, we didn't have any |
|
| 48:06 | cake, we didn't have any anomalous physical properties close to the uh Warhol |
|
| 48:13 | . We just had the formation. of course for realistic problem you want |
|
| 48:18 | have in your model in your analysis some representation of the mud cane. |
|
| 48:24 | might be like an inch or so uh walk with reduced porosity and so |
|
| 48:36 | velocity because of the particles. Yeah there might be tortoiseshell modes now. |
|
| 48:50 | I have to say something about Oh normally when we um have a |
|
| 49:01 | tool in the more home. Normally it does is it puts a pulse |
|
| 49:07 | sound from the tour um out from tool towards the borehole wall and it's |
|
| 49:14 | same in all directions. We call a monopoly source. It's going to |
|
| 49:18 | a P wave wave. Of course propagates through the mud towards the borehole |
|
| 49:25 | . And it'll have a suitably high tool designer will arrange so that emitting |
|
| 49:33 | waves through the but with appropriate velocities we'll talk more about what that means |
|
| 49:45 | yourself. But then starting about 30 ago they um developed another kind of |
|
| 49:56 | of Leipold source which does not radiate equally in all directions. What it |
|
| 50:05 | is it emits a P wave in direction with a positive pulse and at |
|
| 50:11 | very same time it sucks in mud the other side. So what happens |
|
| 50:16 | the p wave propagates out the other or the negative polarity. Okay, |
|
| 50:22 | when those waves hit the uh borehole uh one of them kicks the borehole |
|
| 50:29 | to the left and the other one the borehole right wall to the right |
|
| 50:36 | that makes a traditional way of the itself is uh It's been in a |
|
| 50:45 | way and that deformation travels up and the more whole uh with its own |
|
| 50:52 | , uh which international mode um as says here and then what uh the |
|
| 51:02 | they do that is because further up bar hall, they have receivers and |
|
| 51:08 | receivers receive their especially designed to receive partial modes. And we'll talk in |
|
| 51:17 | seven about why they did about 30 ago. It was a big advance |
|
| 51:23 | a reason. That's obviously gonna make sorts of complications for the tube waves |
|
| 51:29 | well. And then uh we've ignored ice hockey. Of course, a |
|
| 51:35 | complication would have to include an eye . So that's all I want to |
|
| 51:42 | about two boys. So, uh do a quiz here. Let me |
|
| 51:48 | to you. Uh Miss Del Uh we got a B C and |
|
| 51:54 | says all of the bus. So soon as you see that you're gonna |
|
| 51:57 | alert, that d might be the , but maybe not. So, |
|
| 52:01 | question says, the quasi cylindrical shape a four hole naturally introduces uh a |
|
| 52:09 | a one day propagation of surface, that correct? Yes. And being |
|
| 52:16 | , is that correct? Yes. so the applause in operator in cylindrical |
|
| 52:22 | has solutions which are not plane but our vessel functions. And so |
|
| 52:27 | C. So we got a B C are all true. So the |
|
| 52:32 | . Now, long question, true false. Read it for yourself. |
|
| 52:37 | , I'll read it realistic really waves the Earth's surface like we discussed yesterday |
|
| 52:45 | out in two dimensions, meaning that amplitude decreases rapidly with austin uh losses |
|
| 52:54 | the two horizontal directions. By Sudo rarely waves on a borehole sort |
|
| 53:00 | spread out in one dimension only along borehole as we talked about so that |
|
| 53:05 | amplitude decreases more slowly with lawsuits. these statements true or false? |
|
| 53:15 | Yeah. I call that trip. are good now. So that brings |
|
| 53:22 | to the end of the of the concerning surfaces. So we've learned uh |
|
| 53:34 | we thought after studying body waves. that's all good. Uh P waves |
|
| 53:38 | S waves were done but now we out that there are more solutions complicated |
|
| 53:45 | uh because of the surface of the . And what makes it complicated is |
|
| 53:52 | the boundary conditions which we did not and discuss before uh work so that |
|
| 53:59 | waves travel with surface wave velocities not not VP not Bs but the surface |
|
| 54:05 | velocities more complicated and more over And then we talked about the particular |
|
| 54:14 | waves. Hello waves and we talked worlds and uh how uh similarities coming |
|
| 54:26 | there's a surface there but there's also um by the cylindrical insurance. And |
|
| 54:38 | all of this has prepared us now this topic, reflections and refraction which |
|
| 54:46 | uh the most important part of our in this business. Um Sure, |
|
| 54:58 | we're gonna do at this point is this is a good time for a |
|
| 55:04 | yes, Excellent planning. So let's for uh break for 15 minutes and |
|
| 55:12 | come back at 9:45 and I'll uh my audio video in the interim and |
|
| 55:24 | be getting and I'll see you in minutes topics floor. Look at these |
|
| 55:32 | that we've already covered here. It's of like the basics and this is |
|
| 55:37 | very important, reflection and refraction is of the dominant role that reflections play |
|
| 55:43 | exploration, geophysics. I should remind that reflections are not so important for |
|
| 55:50 | seismology and global seismology, they're much interested in re fractions And but because |
|
| 55:57 | that, when you get done with , uh you'll think, okay, |
|
| 56:02 | all there is. Uh that's uh the important stuff. But look what's |
|
| 56:07 | next. A bunch of complications, of different complications. And then discussion |
|
| 56:14 | topics which we've ignored so far, have we've ignored so far the boards |
|
| 56:21 | the rocks, we've ignored the fact Attenuation and we've ignored the fact that |
|
| 56:26 | ice age. So that reminds but we are going to deal with |
|
| 56:31 | because of Mr Einstein. So, has on her wall in that |
|
| 56:39 | she has a quote from, I this is my favorite quote from |
|
| 56:42 | everything should be made as simple as , but not simpler. And of |
|
| 56:47 | she was talking there about the formulation the most basic laws of the |
|
| 56:53 | but we can apply this, lose to our business as well. Uh |
|
| 56:58 | we have looked at so far as applications of simple ideas and now we |
|
| 57:06 | uh and that was good according to , but if we stop there, |
|
| 57:11 | violating the wisdom of Einstein, because would be uh too simple an analysis |
|
| 57:20 | sufficient to understand our date. so that I want to um start |
|
| 57:29 | next topic, reflections and refraction. , so can I get some feedback |
|
| 57:40 | ? Uh people see the introductory slide less than six? No, we |
|
| 57:48 | see the outline from the last Okay, so what I have to |
|
| 57:54 | is um I have to get Stop sharing. Start sharing. |
|
| 58:04 | and I think maybe you didn't even the quote from Einstein. Uh am |
|
| 58:10 | correct? No, I just thought were reading it. Yeah, so |
|
| 58:14 | a quote from Einstein, Can you that? Okay, everything should be |
|
| 58:19 | as simple as possible, but not . Okay, so now I'm gonna |
|
| 58:24 | stop sharing and start sharing. Didn't that right before, so now you |
|
| 58:35 | see the interest lied for less than , is that right? Yes. |
|
| 58:43 | , so uh so here's what we're learn in this lesson, you'll um |
|
| 58:54 | be able to explain to other what are the boundary conditions at reflecting |
|
| 59:00 | , how these results in its simple for normal instance, planer us much |
|
| 59:07 | complicated formula for obliquely. So this what we normally have. This is |
|
| 59:11 | kind of data that we normally look , where the source receiver offset. |
|
| 59:16 | means the waves are traveling obliquely through medium, oblique to the to the |
|
| 59:22 | the reflector. And so that's an thing. And uh very complicated |
|
| 59:29 | But we do not follow Einstein's We do not uh think in terms |
|
| 59:35 | these complicated formula, but we simplify equations for the common case of weak |
|
| 59:42 | on either side of the reflecting And when we but we also need |
|
| 59:49 | consider the special case of the free . And we have to uh we |
|
| 59:57 | to understand the special case when the is very large. Uh See back |
|
| 60:03 | here, we started with normally instant and when my father was a |
|
| 60:09 | performing back in the thirties and the um uh that's all they looked |
|
| 60:16 | They didn't have the idea early on they should have a separation between the |
|
| 60:22 | and offset and everything was more primitive and and so as they learned over |
|
| 60:27 | years, they said, hey, have source receiver offsets. Uh and |
|
| 60:35 | impact those reflect those reflectors were at angles. And will that be |
|
| 60:41 | And uh I think you probably already why that's useful. Uh but ever |
|
| 60:49 | then we've sort of operated on the that the, the angles of incidents |
|
| 61:00 | not zero, but they're not very . And so we can often get |
|
| 61:04 | with assuming hyperbolic move out and then we wanted to do further offsets. |
|
| 61:11 | see the progression here, We wanted do further offsets so that we needed |
|
| 61:16 | have non hyperbolic move out corrections. now here we're gonna uh think about |
|
| 61:24 | happens when the angle of incidence is large. And then we also need |
|
| 61:30 | think about what happens uh when the wave is not a plane wave. |
|
| 61:36 | I right up here, it says waves, but you know that actually |
|
| 61:41 | waves are all, all of them . So what impact does that have |
|
| 61:48 | our analysis? And then truth to is not true that all reflecting interfaces |
|
| 61:55 | perfectly uh straight. Uh not only they not flat, they're they're also |
|
| 62:02 | . For example, if you have dipping flat interface, that's a complication |
|
| 62:08 | we talked about a little bit But what happens if the interface is |
|
| 62:13 | ? So, uh, you know um reservoirs are frequently contained within anti |
|
| 62:21 | structures means its structure in the surface the dome. And the structure gets |
|
| 62:27 | off to the sides and the oil at the top of the dome because |
|
| 62:31 | a lighter density than the bride. it kind of works its way to |
|
| 62:36 | top of the antique line. So there, you should be thinking |
|
| 62:44 | if it's a curved surface, can get away with ignoring that? And |
|
| 62:49 | only about the way uh only about on flat interface. And the answer |
|
| 62:58 | , well, you'll see the Okay, so that's the program in |
|
| 63:04 | . So the first thing is boundary . So, Uganda conditions at a |
|
| 63:10 | elastic innocence. So let's think about uh this scalar wave equation for the |
|
| 63:18 | potential looks like this. We've seen so many times now and you know |
|
| 63:23 | this velocity uh the way it's gonna a p wave velocity here, since |
|
| 63:29 | dealing with a scalar wave equation. this velocity turns out to be the |
|
| 63:34 | of the waves, not the velocity the particles within the wave velocity of |
|
| 63:39 | wave itself. And that's notation as derived it, that's a conclusion. |
|
| 63:45 | we first introduced this symbol as notation this ratio where M is K plus |
|
| 63:52 | thirds new. And we talked about how he never appears by itself in |
|
| 63:58 | wave equation in in a wave Always in the combination with K plus |
|
| 64:05 | new. So that's why we give a name. Mhm. We also |
|
| 64:11 | from previous work and solutions are going be a sum of plane wave terms |
|
| 64:15 | this. So they can be going any direction that's determined by the wave |
|
| 64:21 | K. You can be going up down. And because of this, |
|
| 64:26 | hear it oscillates. It does not increase with time uh to grow infinitely |
|
| 64:38 | small. It oscillates because of I and also we talked about the |
|
| 64:43 | that uh this is a complex number the data of course are gonna be |
|
| 64:48 | . So we talked about how in end when we some of these things |
|
| 64:52 | , we're always going to end up a real observable, but it's very |
|
| 64:58 | for us to talk using this complex , not have to we don't have |
|
| 65:06 | um consider that the sign and the sign solutions uh This way because separately |
|
| 65:17 | all gonna sum them up later. is the relationship between the vector and |
|
| 65:27 | frequency? Uh Mind you, it affects the magnitude of the way affected |
|
| 65:36 | of these things of these components Only the magnitude and um is a |
|
| 65:45 | wave velocity and the angular frequency. , suppose such a way that incident |
|
| 65:54 | elastic, this company, here's the wave vector. It's gonna be solving |
|
| 66:02 | this equation in the upper medium and uh anticipating a later result, some |
|
| 66:09 | it's gonna transmit down here. So so we uh say that uh that |
|
| 66:15 | of a way propagating in the lower , it's gonna have a very similar |
|
| 66:20 | and the main and the difference is here uh the physical parameter is different |
|
| 66:26 | uh it's gonna turn out to we have to specify for this |
|
| 66:33 | both the velocity and the density in . So we can expect to find |
|
| 66:43 | wave solution just like we uh showed slide and they're gonna have coefficients in |
|
| 66:50 | spectral coefficients family of solutions on both . And uh we are going to |
|
| 66:57 | those coefficients, determine those professions, that Bill Bay boundary conditions right |
|
| 67:04 | Okay, obviously we're gonna call this Z people zero at three equals now |
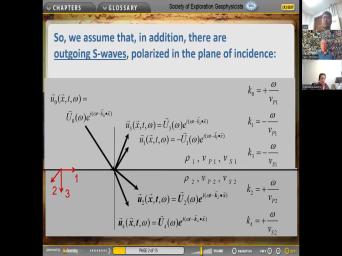
|
| 67:12 | we have an interface here. Uh interface has a normal uh normal vector |
|
| 67:19 | in the X direction in this case of that surface. Uh the problem |
|
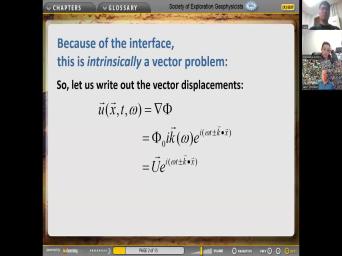
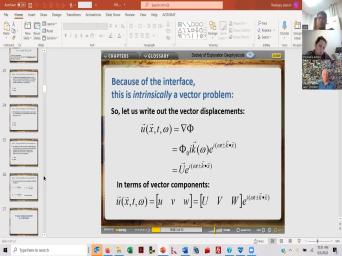
| 67:25 | intrinsically a vector problem. So let's out the vector components which are the |
|
| 67:32 | of that Scaler. And so when make this gradient operation on the |
|
| 67:37 | it uh takes the derivative of this function and it uh primitive uh brings |
|
| 67:46 | the exponential function because of the magical of the oil number E. And |
|
| 67:52 | in front of it here we have . And vector K which comes from |
|
| 67:57 | differentiation of this part of the expo of course this part is independent of |
|
| 68:03 | . So that was so we're gonna this rector here with Scaler uh platoon |
|
| 68:13 | an imaginary uh oh two minus one here and vector K. Here gonna |
|
| 68:20 | all that together vector U. Upper you And um it's got uh um |
|
| 68:32 | components like that. So the three of the vector locus you are given |
|
| 68:36 | hair and notice here that uh you written without a vector markets uh order |
|
| 68:45 | then for the uh the amplitude part it out this part here uh uppercase |
|
| 68:51 | . V. And W. And this one shows the exponential factor separately |
|
| 68:56 | this one doesn't. Yeah. So boundary conditions are we going to apply |
|
| 69:02 | ? So these boundary conditions, I remind you are not additional ideas, |
|
| 69:08 | can prove that these are the right conditions by analyzing the wave equation |
|
| 69:14 | not something new that will spring on . Uh And so the result of |
|
| 69:20 | kind of analysis says that the displacement be continuous across the interface at all |
|
| 69:26 | . Otherwise the material would be torn the way, that's not the kind |
|
| 69:29 | solution we want. And uh so it is, all these components must |
|
| 69:36 | continuous secondly, the stress components of towel I three stress venture, that |
|
| 69:45 | all the components of the stress which aligned with the interface must be |
|
| 69:53 | If that weren't true, the vertical of stress which appears in the wave |
|
| 69:58 | would be interested. And so the at the surface would be infinite. |
|
| 70:03 | don't mind if there's a finite uh a finite acceleration of that service. |
|
| 70:12 | don't mind if the service wiggles up down in response to the way, |
|
| 70:17 | just don't want to be instantly um Um as you understand that uh grading |
|
| 70:26 | stress is the acceleration and so um the gradient has a jump in, |
|
| 70:33 | there's a discontinuity then right there at interface, the gradient of stress would |
|
| 70:38 | infant acceleration would be infant and have . And so here we have the |
|
| 70:46 | are all uh these five components of stress factor of the stress tensor must |
|
| 70:54 | continuous across the boundary and putting in law. Uh 13 components of |
|
| 71:04 | That's uh cookie and stiffness tensor or 13 for the first two industries, |
|
| 71:12 | as we have here and all the and all the else. Uh multiplying |
|
| 71:17 | all the epsilon chaos uh Nine different on the right here in general. |
|
| 71:23 | gonna simplify of course. Uh That's is putting hooks law in and the |
|
| 71:30 | thing down here for the other. , so there's still real. Is |
|
| 71:38 | statement true or false? I feel it's fall. You are correct. |
|
| 71:49 | continuity of stress and displacement. Very for students to forget that and think |
|
| 71:57 | and strain uh trips off the tongue easily, but that's not what we |
|
| 72:04 | that we just showed that stress and . So that statement is false about |
|
| 72:10 | . Is that true or false, . And why is it false? |
|
| 72:25 | it, Read it carefully. Uh it a discontinuity? Say it |
|
| 72:37 | I didn't hear you. Oh no, it's true. Yeah, |
|
| 72:43 | one is true for the display shin but now here's the core, here |
|
| 72:49 | the corresponding question about stress and that's I think you were thinking about when |
|
| 72:53 | first answered false. So this one false because only certain components of stress |
|
| 72:58 | to be continuous. Uh Those components are aligned with the surface itself in |
|
| 73:06 | to have a 31 of the at least one of the indices of |
|
| 73:11 | stress uh is included in that So so those components, the five |
|
| 73:17 | of stress which are have one of indices or three, those have to |
|
| 73:26 | continuous. And we didn't say anything the other components. Okay, so |
|
| 73:33 | that we understand the boundary conditions, think about the simplest case. Um |
|
| 73:39 | the simplest case because we we are to have rocks on either side of |
|
| 73:43 | boundaries. So the simplest case you know, have air up |
|
| 73:47 | but for an interface inside the earth we're going to consider um normal. |
|
| 73:58 | so uh we have only the displacement also gonna be vertical. So we're |
|
| 74:04 | call that lower case w and it's be a function of position time and |
|
| 74:09 | gonna have its own frequency. We change that later, but uh frequency |
|
| 74:17 | zero. And uh we know it's plane wave solution. So the solution |
|
| 74:23 | like this with uh an amplitude um the uppercase w which might also be |
|
| 74:35 | function of omega. And how are two items related together? Well, |
|
| 74:44 | we are gonna say that Kcm zero in mega zero divided by the |
|
| 74:51 | That's the same velocity we have and we have a plus sign. |
|
| 74:55 | what that means is that um uh with this minus sign, with this |
|
| 75:05 | sign. Uh This means that the is going down as time increases. |
|
| 75:13 | got to have X3 increasing in order keep the phase constant. And so |
|
| 75:20 | that means that this wave is going like it showed here. So this |
|
| 75:26 | sign and this one here uh gotta , we have to have the right |
|
| 75:33 | are right here. Now let's assume the boundary conditions that we just said |
|
| 75:41 | a reflected and transmitted wave and that a guess which we are gonna validate |
|
| 75:49 | . So the upcoming wave is gonna like this. Now, let's uh |
|
| 75:54 | look carefully. We got subscript one everywhere. We distinguish between the incident |
|
| 76:00 | and the reflected wave. And we a minus sign here, where we |
|
| 76:05 | corresponding a plus sign here. So uh is a standard convention. Let's |
|
| 76:11 | so that the um um displacement is well, we're gonna use that as |
|
| 76:23 | convention. We could choose another convention I got to tell you that over |
|
| 76:27 | years, many people have tried to creative at a point like this. |
|
| 76:32 | and they've always gotten into trouble. we're gonna follow the standard conventions have |
|
| 76:37 | minus sign out here and a minus here, but Uh the K one |
|
| 76:45 | gonna be negative. So together with minus sign, and this minus sign |
|
| 76:51 | the wave is traveling couples. And now here is the transmitter wave |
|
| 76:57 | we're gonna have subscriptions to everywhere. again, this is going to have |
|
| 77:03 | positive. Um not gonna have an minus sign here, just like we |
|
| 77:10 | here, because these waves are traveling , these two are traveling down. |
|
| 77:14 | that that means we're gonna want to a plus sign here, just like |
|
| 77:19 | had here. And again, we the minus sign here in the |
|
| 77:24 | But again, we have plus sign , just like we did here, |
|
| 77:28 | pay attention to uh screw up any these sign conventions get into trouble. |
|
| 77:35 | this is um a consistent set of . Yeah. What we need then |
|
| 77:47 | we need to solve for these two W one, W two. And |
|
| 77:51 | uh frequency Omega one. And we're use the boundary conditions here to match |
|
| 77:59 | solutions on this side. And on side, stop that. Um at |
|
| 78:09 | surface, which is uh X equals . The tangential components of displacement are |
|
| 78:15 | zero just by symmetry. This is vertically traveling p waves. So that's |
|
| 78:20 | , but for the normal part we to add together the displacements in the |
|
| 78:28 | part that's incoming and um reflected and those have to be the same as |
|
| 78:36 | single. Uh That that song here gonna be the same as single wave |
|
| 78:45 | war medium. And you notice here no Z here appearing no X three |
|
| 78:50 | because we were soon X 340. we can find a solution to this |
|
| 79:00 | at all times only if the frequencies all the same. So let's just |
|
| 79:05 | the subscription and all that will So this will be the incoming wave |
|
| 79:11 | frequency omega and absolutely necessary that reflected transmitted ways have to have the same |
|
| 79:21 | . Then uh we can divide out exponential terms and I just want to |
|
| 79:29 | back here so that that some comes some of this thing plus some of |
|
| 79:37 | thing and the minus sign is already explicitly. That's why this minus sign |
|
| 79:43 | here. Okay, now the continuity stress. So uh let's talk about |
|
| 79:53 | 13 stress and uh oh So what says is uh 13 stress. You |
|
| 80:13 | mhm carry out the sum from hook's and you find the only terms in |
|
| 80:19 | are surviving are the ones which have three here and 13 year. These |
|
| 80:26 | all the same because of the symmetry . That gives you a two right |
|
| 80:30 | summing those two together and the common for this component of uh tensor is |
|
| 80:38 | not the common name in two component , it's a C 55 because 13 |
|
| 80:45 | 31, both of them up to five. When we switch to the |
|
| 80:50 | components Rotation and the definition of strain given like this. And so this |
|
| 80:57 | that it's got here you one that's in the horizontal direction, we know |
|
| 81:02 | zero because of this is normal so that 10 and this is a |
|
| 81:09 | in the one direction. So that's a zero. So I got uh |
|
| 81:13 | plus zero here. So never mind this stuff. It all gets multiplied |
|
| 81:18 | zero right here and parenthesis. And that's gonna be true for each |
|
| 81:24 | incident mode reflected and transmitted mode and same thing down here for 23 |
|
| 81:32 | And for the 33 express we carry the sum and uh so we get |
|
| 81:37 | 3311 term, that's a non zero in the tensor and all that. |
|
| 81:45 | uh and to index notation we're gonna that C 31 and here's a C |
|
| 81:53 | coming from this C 33 coming from and the epsilon terms are gonna involve |
|
| 82:02 | in the one direction. So that's be a zero here are changes in |
|
| 82:05 | two directions. That's gonna be And the only thing that survives after |
|
| 82:09 | this um something and so on is one in the three direction And the |
|
| 82:15 | name for this sensor, This matrix . So that's got to be continuous |
|
| 82:23 | the area. Yeah street in the wave. So here is uh super |
|
| 82:30 | here stands for incoming and we've got . So here's the incoming displacement in |
|
| 82:37 | vertical direction. And it um it applying the launch monitors em in the |
|
| 82:44 | medium. So all we're doing is this equation, the incident wave in |
|
| 82:51 | upper medium. And so uh we adopted the uh notation that this vertical |
|
| 83:01 | is given by more case W and zero reminds us that's the incoming |
|
| 83:11 | And from the previous page we're gonna that is a lowercase W This |
|
| 83:17 | Uh Thank you here and let me . Right when we do distributive, |
|
| 83:35 | down out of the exponential of minus K. Zero minus I K. |
|
| 83:41 | that appears here. So collecting all together. Uh Now what I wanna |
|
| 83:52 | is uh change uh notation, know M1 is uh You can be represented |
|
| 84:01 | terms of density and velocity in this we know that K-0 can be represented |
|
| 84:06 | terms of frequency and velocity in this . These are old ideas for you |
|
| 84:14 | . And uh collecting terms we get a density times velocity of the first |
|
| 84:22 | and here's the frequency right in here do that similar for the other two |
|
| 84:28 | . And it looks very similar. uh in a sign here which comes |
|
| 84:34 | our previous conventions. You can verify for yourself, the minus sign |
|
| 84:39 | that comes from our previous convention, that for yourself. And then what |
|
| 84:46 | have to have the stress that stress the incident way plus the stress from |
|
| 84:50 | reflected way that's happening in the upper and low medium. We have this |
|
| 84:58 | combining with the first equation we got displacement continent, we find this |
|
| 85:05 | So the ratio of the reflected the incident amplitude given by this difference |
|
| 85:13 | by this sum. And that is we call the p wave reflection coefficient |
|
| 85:22 | , correspondingly we have the transmitted Anderson by the incident amplitude is given by |
|
| 85:30 | minus this. And we call that transmission coffee abnormal answers. So these |
|
| 85:38 | should be familiar to you, although might have forgotten the derivation. So |
|
| 85:45 | derivation that I gave you um is good one. And it depends up |
|
| 85:50 | our making the right um conventions for the various minor signs have to show |
|
| 86:01 | notice here that the frequency has uh out this frequency hidden inside here and |
|
| 86:12 | inside here. Um No uh but frequency already canceled out at this |
|
| 86:19 | All of these have the same So these results are independent of |
|
| 86:24 | That's really important. So the reflected is gonna come up with the same |
|
| 86:33 | as the uh incident media. And when you add together all the plane |
|
| 86:39 | like this, that means the the reflected wave is gonna look just |
|
| 86:45 | incident wave. Except that it's gonna uh why not? Instead of going |
|
| 86:52 | ? And but it has the same of the wave, it's gonna have |
|
| 86:56 | different amplitude, it'll have its amplitude by this. And so this is |
|
| 87:01 | be a normally a small number because this product in the Uh upper medium |
|
| 87:10 | going to be pretty similar to this in the lower media and the difference |
|
| 87:14 | gonna be small compared to the And this is normally going to be |
|
| 87:19 | small number of the order of 10% less. And it could be positive |
|
| 87:24 | negative C. Haven't said here, are these is bigger. Now this |
|
| 87:32 | we call them peaks and we give the conventional notation uppercase Z. So |
|
| 87:39 | the previous result in this way Z . P. To the upper |
|
| 87:45 | zp two in the lower media minus . P. One in the upper |
|
| 87:51 | divided by the sun. And it's for you to remember which which of |
|
| 87:56 | is which the incident medium has the sign in china. So this jump |
|
| 88:03 | delta Z. P. Simply this you can recognize this sum is |
|
| 88:10 | Yeah. Normally the reflection coefficient is lot less than one. So normally |
|
| 88:20 | the transmission coefficient is functionally equal to because this number is small. Not |
|
| 88:29 | . And that's a good thing if we had most of the energy reflected |
|
| 88:34 | only a small part transmitted. That be bad because we couldn't see very |
|
| 88:39 | into the earth. And lucky for normally the reflection coefficient is small and |
|
| 88:47 | , so most of the energy continues past. Mhm. Perfect. So |
|
| 88:55 | other words like that one at a time. So here's our results. |
|
| 89:03 | you notice that if the lower uh impedance is greater than the upper impedance |
|
| 89:10 | uh jump is uh greater than And so the reflection coefficient is greater |
|
| 89:18 | and the transmission coefficient is less than . However, if the jump in |
|
| 89:27 | negative then the reflection coefficient here is be negative. That happens when Z |
|
| 89:34 | two is less than zp one. uh slower uh lower impedance below, |
|
| 89:42 | mp and survive. So in that the reflection purpose is negative. And |
|
| 89:48 | the transmission coefficient right here is greater one more amplitude goes down and comes |
|
| 89:57 | . How is this possible? So uh Miss del rio, have you |
|
| 90:04 | considered this straightforward consequence of these equations which you're presumably you're familiar with this |
|
| 90:13 | right here and both these results. did you ever think that when you |
|
| 90:20 | uh negative jumping and beating, you're have a transmission car efficient? Greater |
|
| 90:28 | one, like it says here or goes out than comes in. Have |
|
| 90:33 | ever thought about that? Does does it trouble you? Little |
|
| 90:39 | Yeah, it is weird. but it's so easy to see where |
|
| 90:44 | comes from. And you know that the Earth there's lots of alternating velocities |
|
| 90:54 | , and alternating densities as you go through the layers. So this must |
|
| 90:58 | a lot. Well, like you , it's weird. So let's think |
|
| 91:04 | uh just how weird this is. , uh, let's think about the |
|
| 91:09 | density. The energy density has is in this way. And uh we |
|
| 91:17 | about this um, several lectures I won't repeat that. Just remind |
|
| 91:21 | of what we have on the left a scale or by the way, |
|
| 91:25 | , this you is now energy, displacement. And I need to use |
|
| 91:30 | different location. The same notation we before for energy density. And now |
|
| 91:38 | forgot when I wrote it this that it's um, uh it looks |
|
| 91:43 | much like the displacement coefficient there just find 10 minutes ago, I'll go |
|
| 91:51 | and change. But this is the stiffness um, sensor that we had |
|
| 91:58 | and the same strains we had And this is a scalar. And |
|
| 92:01 | we have to do sums over I J and eminent lots of sons. |
|
| 92:06 | so, uh, these vertically traveling waves for each mode, it all |
|
| 92:14 | . So it looks like this. got only 33 strains. And we |
|
| 92:18 | only the C 3333, right So that's true for each moment. |
|
| 92:25 | so putting in right here, the common name for C. 333, |
|
| 92:31 | in right here the definition of Uh and then taking this derivative, |
|
| 92:36 | got an I. K. Um like a w. And it's squared |
|
| 92:42 | we have this product here. And that square makes a -1 and multiplied |
|
| 92:48 | this minus. So here's a Right here we put in the definition |
|
| 92:54 | em in terms of velocity. And here we put in the definition a |
|
| 92:59 | terms of they got, he seeing all that out, we get |
|
| 93:08 | omega rho omega squared divided by two . Um So that's the energy gen |
|
| 93:21 | each mode and from the square of frequency and the square of the uh |
|
| 93:30 | uh amateur. And um right here have uh solitary factors, also inside |
|
| 93:39 | invention of the first pound. And see where the two. So that's |
|
| 93:45 | energy density. Now we ask about energy flux for his mouth, so |
|
| 93:49 | uh that uh energy density is traveling this philosophy. And so uh energy |
|
| 93:57 | is going to be given by this part will just drive. So |
|
| 94:06 | we're gonna ask, is that energy across the boundary concern. We have |
|
| 94:11 | same amount of energy coming in as out downwards. And uh you're saying |
|
| 94:21 | wrong, we have to have the on the left hand side of the |
|
| 94:25 | flux and the and the reflective flux On the upper part of the medium |
|
| 94:33 | , is that equal to the transmitter in the lower media? If it's |
|
| 94:38 | equal then that means that energy is to be left behind at the |
|
| 94:44 | And if all the definition means the is gonna be heating up because of |
|
| 94:49 | incidence of this way. So that better find out that these um um |
|
| 95:00 | works out. We better find that flux on one side equal fox on |
|
| 95:05 | other side. So putting in the results that we just found uh same |
|
| 95:14 | mark here, uh huh The same that we just asked, it was |
|
| 95:23 | and then simplifying that equation uh by for yourself here and work out the |
|
| 95:31 | figures out, you will see the to this question right here is |
|
| 95:35 | we get the same energy flux on sides of this equation. Whether or |
|
| 95:41 | The transmission car fishing is lasting So energy is conserved within the |
|
| 95:50 | The same amount of energy is going the surface as coming out of the |
|
| 95:55 | , reflected and transmitted. So the does not yet hot, does not |
|
| 96:01 | cold. All the energy is retained the um in the wave. And |
|
| 96:11 | what that means is that uh the that the amplitude in the transmitted wave |
|
| 96:18 | be bigger than the aptitude and the incident wave, that's okay because it's |
|
| 96:26 | energy flux is dependent on this. uh this expression here? No it's |
|
| 96:38 | the amplitude. Uh it's the energy is important, you see right |
|
| 96:43 | this product same as we have And um so the fact that we |
|
| 96:56 | higher aptitude going out on down is a problem using this energy. |
|
| 97:08 | Wait, so MS del rio, this true or false? Careful, |
|
| 97:26 | is true. This is the weird . Yeah, this uh this is |
|
| 97:31 | so weird. This is sort of definition. Um uh The first part |
|
| 97:36 | it is the definition here. It the direction of propagation is given by |
|
| 97:40 | gradient of the phase. Yeah, uh I just say is now reading |
|
| 97:49 | carefully and um so it's a trick here, The gradient of the |
|
| 98:01 | Since with negative the way advances in direction of increasing spatial coordinates, uh |
|
| 98:09 | increasing X three. Um uh that is true. Mhm Go back |
|
| 98:25 | review previous slides and see that ingredient negative. Yeah, the wave advances |
|
| 98:35 | the direction of increasing That's true. might want to review previous items |
|
| 98:47 | Um is this true? The attitude a continuous plane wave is given by |
|
| 98:52 | magnitude At the time space position where phase is zero. Okay, so |
|
| 99:01 | think we didn't talk about that What I want to do at this |
|
| 99:05 | ? Go back out of this, did something bad here. So let |
|
| 99:14 | share the screen. Can you see screen again? Yes and select people |
|
| 99:28 | here And so we can use this slide uh you can see where slightly |
|
| 99:53 | . And so here is our it's creating the phase vector and the |
|
| 99:58 | this thing up here. So if zero then the uh the amplitude of |
|
| 100:03 | waves, simply by the amplitude of vector here and talking on the scale |
|
| 100:08 | components only traveling in the X3, this only and this is zero. |
|
| 100:13 | this is because phase is zero, d to the zero. So that's |
|
| 100:19 | one answer. The answer to the is that's false. Um So did |
|
| 100:34 | miss something, explain your reason? , phases zero. I'm sorry, |
|
| 100:41 | was thinking about everything. Never it's true. So when we have |
|
| 100:45 | zero here, that means each of zero, which is one. And |
|
| 100:49 | that means that and at such a , such a place of action, |
|
| 100:56 | the the amplitude of the wave is to the stellar amplitude that we have |
|
| 101:01 | here. Okay, fine. so I'm gonna go in presentation uh |
|
| 101:21 | excited. That one. Yeah. is measured in the same direction as |
|
| 101:30 | way affect. Yeah, that's If the deficit is positive, the |
|
| 101:35 | at Phase zero is parallel to the that no matter what direct. So |
|
| 101:39 | I want you to go back and at our our sign conventions where we |
|
| 101:45 | minus signs scattered around here and there decide for yourself whether this is |
|
| 101:51 | If all I think it's true. I if I recall correctly, that's |
|
| 101:56 | . And you verify for yourself, Stephanie whether or not this is true |
|
| 102:02 | by looking carefully at sign convention that showed on those. Yeah, this |
|
| 102:12 | important. You gotta get this one , tell me which one it is |
|
| 102:27 | . Yeah, a lot of I have to get this one |
|
| 102:32 | Um This one is it's the minus top minus has got to be on |
|
| 102:50 | and it's gonna be either this one this one. And you got to |
|
| 102:53 | the difference here. It all is has uh the incident medium here and |
|
| 102:59 | medium here. So you're right, lot of pressure but you did. |
|
| 103:05 | , okay, so um that's an problem. But it's not our |
|
| 103:11 | We've we've got to find almost all our data is obliquely incident. So |
|
| 103:17 | situation and we got an incident way looks like doesn't So now the difference |
|
| 103:22 | is that a zero is a vector the amplitude of it Is given back |
|
| 103:29 | or make our VP one that's a way upon at some angle. Theta |
|
| 103:38 | um You know what uh Uh it's 1030 is that now passed into I |
|
| 104:02 | this is a good time for us take a quick break. Um Want |
|
| 104:07 | go back to this right here. take a 10 minute break And come |
|
| 104:13 | in 10 minutes and we'll take up topic which is going to be |
|
| 104:18 | So it's a good time for a . So I will um stop sharing |
|
| 104:27 | I will stop my video here. , So I assume that both of |
|
| 104:36 | can see the screen, give me feedback. Ok, so now this |
|
| 104:43 | uh an important topic for us. I'm gonna put us into presentation mode |
|
| 104:51 | here's the situation where we have uh same uh medium above and below and |
|
| 104:59 | have this wave incident and we talked how this is uh uh has uh |
|
| 105:06 | vector k zero up here. And the length of it is given by |
|
| 105:11 | omega over V. P one. reflected wave is going to be over |
|
| 105:17 | somewhere and we don't know yet that theta one is not equal to theta |
|
| 105:24 | , We're gonna discover that. And length of this vector uh is gonna |
|
| 105:30 | um uh have the same minus sign uh and as we have the form |
|
| 105:36 | have a minus sign here and we have the minus sign here and we're |
|
| 105:41 | have a transmitted wave similar with the plus sign here as here. Same |
|
| 105:47 | sign. Had put a plus sign . Okay, so what we have |
|
| 105:52 | decide then is uh the magnitudes of vectors and the angles because we already |
|
| 106:01 | these omegas, all these omegas have be the same. So let's first |
|
| 106:07 | the issue of the angles. So is the incident wave coming in and |
|
| 106:12 | the wavefront looking like that and the is given here. So uh the |
|
| 106:18 | . So think of this as the of the one peak of the |
|
| 106:22 | And remember this is uh plane wave goes on forever. Science and |
|
| 106:29 | And uh so think of um this one of the peaks and this is |
|
| 106:35 | next peak. And so it's traveling distance in the time delta T. |
|
| 106:43 | it's traveling at three P one. notice as it does, so uh |
|
| 106:47 | wavefront is sweeping across the boundary uh because of the angles involved, it's |
|
| 106:54 | equal to the uh this length here by the sine of this angle, |
|
| 107:01 | trigonometry. So we call this the velocity, which is the actual velocity |
|
| 107:09 | the wave divided by the sine of angle. And uh that is equal |
|
| 107:13 | one over the horizontal slowness. That's definition of horizontal appears. So in |
|
| 107:24 | to match these boundary conditions for all ones and at all times the apparent |
|
| 107:30 | must be the same for all So uh this is the same for |
|
| 107:35 | this is the incident mode, reflected and transmitted mode, they all have |
|
| 107:42 | have the same apparent velocity. And is a special case of Snell's |
|
| 107:50 | So then uh oh, sign of the incident angle is given by extra |
|
| 108:04 | the sign, this is the sign the incident angle. This is the |
|
| 108:08 | of the reflected angle and this is ratio of velocities coming from this |
|
| 108:14 | And so in the upper medium that is the incident velocity and the reflected |
|
| 108:19 | . These are the same in the medium. So that's a one. |
|
| 108:23 | so the sign of the of the mode is equal to the sine of |
|
| 108:27 | mode. Uh so the way it at equal angles. So um that's |
|
| 108:39 | to you or you know that this is why why that's true. |
|
| 108:44 | the sign of the uh transmitter wave going to be different because this ratio |
|
| 108:51 | not equal to one. So here's some examples. And so here we |
|
| 108:57 | a case where the velocity is continually . And uh I got this slide |
|
| 109:05 | professionally in our department and because Snell's as required, this is the statement |
|
| 109:12 | Snell's law in this situation. So the angle is continually increasing in this |
|
| 109:19 | because the velocity is continuing increasing. here here is a case where it's |
|
| 109:25 | decreasing uh as you put down is . So the wave is diving. |
|
| 109:30 | neither one of these situations is very Comments. So let's look at a |
|
| 109:39 | where we have uh some slow So V two is a slow layer |
|
| 109:44 | before is a slow layer following the . And so now the wave looks |
|
| 109:49 | of like this one when it reaches top of this slow layer that refract |
|
| 109:54 | . Then when it goes into another layer, reflect upwards then downwards again |
|
| 110:01 | we four are slower and upwards. uh raft bends down in the slow |
|
| 110:08 | . So that's uh the way the vectors work and the angles work, |
|
| 110:15 | it only affects the wave vectors, the amplitudes of the various smokes. |
|
| 110:20 | we've also got to have continuity of displacement and stress. Uh not all |
|
| 110:27 | but simply these components of stress. that makes two equations here. Two |
|
| 110:34 | here, add them up. Makes equations and all but we have only |
|
| 110:38 | for two free parameters left, which the amplitude of the reflected wave and |
|
| 110:43 | amplitude of the um transmitter wave. so you can't have uh just can't |
|
| 110:53 | these four equations with just two free . And so the proposed solution is |
|
| 111:00 | gonna work, simply not gonna So what we have to do is |
|
| 111:05 | have to assume that in addition there's outgoing share ways. So notice here |
|
| 111:11 | have this uh vector uh shows the um shear wave you three. And |
|
| 111:18 | looks like all these others except that it's got a K three here and |
|
| 111:26 | U. Three attitude vector here. you know that this this vector here |
|
| 111:34 | gonna be uh perpendicular to K3. perpendicular to to you one but it's |
|
| 111:43 | to its own Uh propagation vector. it lies in the 1 3 plan |
|
| 111:51 | . And so uh uh we have all three for all three waves in |
|
| 112:00 | upper media. We have uh these with the corresponding losses, incident wave |
|
| 112:09 | a P wave. That's this one . And so it's related to the |
|
| 112:13 | with VP one that reflected P wave uh involves VP one but it's got |
|
| 112:23 | minus sign here by convention because it's upwards. And uh here is the |
|
| 112:30 | way in the upper media, it's the same minus sign because it's going |
|
| 112:35 | . But it's got a V. . One down here. Sure. |
|
| 112:38 | velocity, shear wave in the upper down here, we have the same |
|
| 112:45 | wave as we had before. And we have a sure way also polarized |
|
| 112:50 | this plane with a wave vector given with plus omega three. S. |
|
| 112:58 | notice the way we've arranged the notation . Oh, industries. Uh even |
|
| 113:07 | are going down 02 and four. are all even The indices for the |
|
| 113:14 | going rates are off one and The wave vectors for the down going |
|
| 113:21 | have a plus plus wave vectors. Wave numbers for the growing waves have |
|
| 113:29 | and of course we have we have include V. S. One here |
|
| 113:34 | V. S. Too but we have that before so we're going to |
|
| 113:40 | able to find solutions only if Snell's extends to all the mod. So |
|
| 113:45 | the apparent velocity for the same for incident wave, reflected P wave, |
|
| 113:52 | P wave, reflected S. Wave transmitted s way so horizontal. Another |
|
| 114:00 | to write this is in terms of horizontal uh slowness, uh whatever the |
|
| 114:08 | velocity is given by this for all and so that's going to determine the |
|
| 114:14 | . So I got some movies for here. Uh you have these movies |
|
| 114:20 | the blackboard I think. Let me if you don't have that. So |
|
| 114:25 | I'm gonna do at this point is thank you. Stop sharing and share |
|
| 114:52 | screen, I wanna show. No want to do that. Um What |
|
| 115:04 | want to do. Yes I'm gonna my zoom. If I lose the |
|
| 115:15 | connection don't worry I'll be back I'm gonna minimize it for Mhm. |
|
| 115:24 | um I lost your knock here, this screen, this screen, this |
|
| 115:40 | and the screen and now I'm gonna the movie. Sure. Mhm. |
|
| 115:57 | can't play in the movie. Oh I'm hoping you can still hear me |
|
| 116:31 | now. For some reason the movie not play. Um So let me |
|
| 116:37 | the other movie to see if that's work and that one says it's not |
|
| 116:52 | . Okay folks I have a problem that I can't show you these movies |
|
| 117:07 | it's a formatting issue. The movies good, I will figure out uh |
|
| 117:13 | sure these movies are playable, I assumed they were playable there. Uh |
|
| 117:19 | format. Um But I have to into that so meanwhile I'm gonna go |
|
| 117:27 | here. So did you all see fumbling now? You probably didn't see |
|
| 117:32 | fumbling around but you heard me fumbling and so I will have to um |
|
| 117:38 | the movies to you uh later and make sure I have workable files and |
|
| 117:45 | sure that you have the right files the out. Uh So where are |
|
| 117:53 | on the blackboard? There should be the same as where you found these |
|
| 118:02 | and if they're not there it means I forgot to put them. But |
|
| 118:05 | okay. I probably would have put inoperable files so I'll sort this out |
|
| 118:12 | over lunch, I'll sort this out be okay. Those are interesting |
|
| 118:19 | Um and uh so we'll get it you. So uh what I want |
|
| 118:28 | do now is share my screen right . Yeah um can you see this |
|
| 118:43 | slide which is where I left you uh so I will also solve the |
|
| 118:52 | problem or lunchtime I use and so gonna put this into mm presentation |
|
| 119:00 | Yeah, so or solving those. so what we're gonna do is put |
|
| 119:10 | guests that I just showed you with five ways incoming and to reflected in |
|
| 119:17 | transform implement the wave equation using those equations for plane waves and solve the |
|
| 119:28 | . So this was done for the time a long time ago and the |
|
| 119:32 | time they did it they got wrong we didn't have a consistent set of |
|
| 119:42 | conventions. And so you might have a little bit irritated by the sign |
|
| 119:47 | that I used. But if you those sign conventions you end up with |
|
| 119:52 | right answer. And uh right answer found by these two. These two |
|
| 119:59 | not considerate. I have a picture of zipper. It's um and um |
|
| 120:06 | equations can be found in many modern . For example the textbooks by AKI |
|
| 120:11 | Richards. Uh So uh do you this textbook, AKI and Richards? |
|
| 120:23 | . So um I know these AKI is now retired from M. |
|
| 120:27 | and richards is now retired from They're both my friends. And uh |
|
| 120:34 | is sort of the standard textbook and and I think 09 was the second |
|
| 120:41 | And the first edition was sometime back the 80s. And so um um |
|
| 120:51 | , do you have this book? do not but I'm going to get |
|
| 120:56 | . It might be a bit advanced you. Uh So but you can |
|
| 121:00 | it cheap on amazon uh and get hard copy edition. Not not a |
|
| 121:07 | copy. And so uh everything that done in this course uh is consistent |
|
| 121:13 | what they show over there. And it's um it's focused on global |
|
| 121:22 | not on exploration technology, but it's a very useful tax standard tax |
|
| 121:30 | So, here is the answer as by AKI and Richards for the p |
|
| 121:35 | reflection coefficient. So look here, a mess this is, or mess |
|
| 121:41 | . And got so much notation. the notation is all um uh listed |
|
| 121:51 | here and it's got layers of So it's got a little uh small |
|
| 121:56 | , A, B, C, D. And then big letters |
|
| 121:58 | F, G, H and And they're scattered all over here. |
|
| 122:02 | this is such a mess that when look at this, your eyeballs roll |
|
| 122:08 | the back of your head. And so um this um was so um |
|
| 122:22 | that for years and years explorations, businesses would not touch it and there's |
|
| 122:30 | reasons not to touch it. Uh can talk about it just without understanding |
|
| 122:36 | really, it involves all six elastic . So three on each side of |
|
| 122:40 | boundary. And but it's a non number. Of course, the reflection |
|
| 122:46 | has to be non dimensional. So must mean that you have to you |
|
| 122:49 | rewrite this in terms of these non parameters. So the ratio of one |
|
| 122:55 | to the other. And then you imagine lots of ways to non dimensional |
|
| 123:00 | , the velocities. Uh here is one of them where you uh invite |
|
| 123:04 | one of these uh four velocities by one. So So there are four |
|
| 123:14 | scattered through there. You can see it's independent of frequency. So it's |
|
| 123:20 | we said uh frequency is going to out of a reflection and it's not |
|
| 123:29 | obvious, but it might be fun you to verify that at normal |
|
| 123:34 | it reduces to the previous result. all those complications go away at normal |
|
| 123:40 | . And it would be a fun for you to prove that to |
|
| 123:47 | Furthermore, if all the angles are , it's the reflection coefficient is |
|
| 123:52 | And uh um all the reflected wave will have the same phase as the |
|
| 123:58 | way. So, I want to back and look at that. We |
|
| 124:02 | all these angles in here, so look real. How could they not |
|
| 124:06 | real? Uh angles here and we've more angles here. And uh you |
|
| 124:12 | that all the angles are frozen There's no uh sign angle in here |
|
| 124:18 | . And uh all those areas. , of course they're real. How |
|
| 124:22 | they not be real? Well, gonna find out that it might be |
|
| 124:26 | of these are not real, not Cozzens. Uh in some instances, |
|
| 124:34 | the incident angle is always gonna be incident angle. So that means no |
|
| 124:38 | of the incident angle is gonna we're gonna find cases where these other |
|
| 124:43 | are not real. Isn't that So that comes later. Now the |
|
| 124:53 | law is given by this and remember we did not require uh we didn't |
|
| 124:58 | to know what the reflection coefficient is for um uh in order to define |
|
| 125:06 | the angles are. So for p angles here it is and solving this |
|
| 125:13 | the transmitted ankle sign data to equal sign of the incident angle with this |
|
| 125:18 | ratio. Yeah so I suppose that lower medium is faster than the |
|
| 125:24 | Um So this ratio is bigger than and then suppose that the sine of |
|
| 125:30 | angle is pretty large uh as we , so so far that incident angle |
|
| 125:38 | be anything. So let's choose a angle so that when you multiply it |
|
| 125:44 | um uh by this ratio which is than one, that means that the |
|
| 125:51 | of state A two is bigger than . You can imagine for large incident |
|
| 125:57 | with uh fast medium over a slow , you can have the case where |
|
| 126:05 | formula implies the sign of state into is bigger than one, wow. |
|
| 126:11 | so the Kassian uh co sign is in terms of the sign in this |
|
| 126:18 | . So if this thing is bigger one then uh we have a negative |
|
| 126:23 | underneath the square root sign. So co sign of data to under these |
|
| 126:29 | is gonna be imaginary, wow. remember we just uh just back here |
|
| 126:38 | said if all the angles are real the reflection coefficient. But now we |
|
| 126:43 | the case right here for some of angles are complex. And in particular |
|
| 126:49 | you have a complex co sign data that uh have a complex angle then |
|
| 127:01 | that case the post sine of that is pure imagination, otherwise it's pure |
|
| 127:07 | . But if in this circumstance you the case uh full sine theta two |
|
| 127:13 | imaginary. Yeah, where does that ? It happens in large large |
|
| 127:20 | And so what how how large is ? Well the where the incident angle |
|
| 127:26 | transitions from real to complex is at place where the sign data to uh |
|
| 127:32 | data to is one. So that to an incident sign at some critical |
|
| 127:39 | multiplied by this velocity ratio. So is that critical angle? It's that |
|
| 127:45 | where the sign is the sign of incident prayer triangle is given by this |
|
| 127:51 | relation. So at incident angles greater this. Many interesting phenomenon occur both |
|
| 128:01 | the reflected and transmitted light. So we don't look at these post critical |
|
| 128:09 | but maybe we should and I'll show , we'll talk more about that right |
|
| 128:19 | so far, we have ignored the of the incident away from and that's |
|
| 128:28 | um and we talked only about plain . Okay, so imagine a curving |
|
| 128:34 | from Mr fourier mr Fournier has guaranteed us that we can describe this curved |
|
| 128:43 | as the summer plain whites. And uh imagine um heard way from advancing |
|
| 128:55 | a certain direction, there's a ray perpendicular to the wave front. So |
|
| 129:01 | an oblique ray and a curving away and that at that particular angle where |
|
| 129:07 | raid direction uh say uh data zero the front. Ordinary front, it's |
|
| 129:19 | be a sum of plane waves. the dominant term in that sum is |
|
| 129:26 | uh the main way, which is parallels and away from that point perpendicular |
|
| 129:32 | the right in the sun. The term is the plane wave um perpendicular |
|
| 129:41 | to the way from tangent to the from at that point. And then |
|
| 129:46 | the other uh terms and that some needed to transform the uh the |
|
| 129:53 | that dominant plane wave into a serving , dominant term is for myself. |
|
| 130:00 | as it impacts a planer um plainer , like we just talked about, |
|
| 130:07 | we needed to talk about was the uh the interaction of that dominant plane |
|
| 130:17 | with the surface. And that's what been doing up to this point. |
|
| 130:21 | . And that works for us for of our data, all we have |
|
| 130:25 | think about these plane wave reflection. fishing's even though we never have plane |
|
| 130:31 | in our data because in the foray uh for the third wave front as |
|
| 130:38 | hits the wave at the circus that I'm gonna determine that for you. |
|
| 130:44 | is um anyway, cleaner way answer the service. So uh we can |
|
| 130:54 | can neglect the rest in most cases close to the source, uh the |
|
| 131:03 | re strong and we might have to include more terms uh there in the |
|
| 131:10 | process close to this source. But we're not worried about reflections close to |
|
| 131:17 | source uh near surface. Normally we're worried about that, but beyond the |
|
| 131:25 | angle near the critical angle, uh have to make a correction uh as |
|
| 131:32 | consider reflections near a critical angle, need to also consider this courage. |
|
| 131:41 | uh so in what follows, we uh add on the assumption that as |
|
| 131:50 | continue to look at a plane wave and transmissions means we're not very close |
|
| 131:56 | the line. Now we saw before very complicated expression or um for the |
|
| 132:12 | coefficient here is the expression for the coefficient in that same situation p down |
|
| 132:18 | incident and transmitted, you can see a lot um simpler, but it |
|
| 132:24 | involve uh the incident angle of And these these coefficients F and D |
|
| 132:32 | were um defined previously and the velocity over the lower medium here, but |
|
| 132:39 | right here, it's got the density the incident meeting. So we figured |
|
| 132:46 | now this is not equal to one reflection coefficient except the normal incidents in |
|
| 132:54 | , you gotta use this term instead was. Now these transmitted waves are |
|
| 133:01 | called refracted waves refracted because you if you're doing an optical experiment or |
|
| 133:07 | shining light on a um for example them um piece of glass, uh |
|
| 133:18 | light transmits into the glass at a angle and all of that is incorporated |
|
| 133:26 | the design of eyeglasses and contact lenses everything like that. And so those |
|
| 133:33 | who design their design those kinds of , all their waves refracted waves and |
|
| 133:41 | the same as this transmitter. Now this is the 21st century, we |
|
| 133:48 | have to consider uh converted coefficient. the version upon reflection. The proficient |
|
| 134:00 | noted like this. See for conversion for incident and expert converted reflected. |
|
| 134:08 | that formula is given by this in of the previous notation. And you |
|
| 134:14 | see immediately from this because it's got sign data out in front, multiplying |
|
| 134:20 | else that's gonna be zero at normal , a normal instance sine theta |
|
| 134:26 | So the conversion coefficient is zero and instance. And furthermore you can see |
|
| 134:32 | if scientist is positive, that's gonna one sign to the conversion coefficient depending |
|
| 134:39 | all this other stuff. We don't necessarily that this minus sign results in |
|
| 134:46 | negative conversion contribution depends on all this stuff. Well but for the same |
|
| 134:54 | In the opposite direction uh we have have a negative uh signed data. |
|
| 135:00 | . So in that case uh immediately that version coefficient is going to be |
|
| 135:07 | symmetric? I have one Uh one for positive process and the other sign |
|
| 135:16 | negative. Normally in our business we consider the transmitted car efficient conversion, |
|
| 135:29 | from P two s and transmission. don't see much of that away in |
|
| 135:35 | data. Um so that's not clear particularly not there. When we first |
|
| 135:44 | looking at ocean bottom, seismic converted 30 years ago. What? Um |
|
| 135:51 | the conclusion that we come to actually at a lot of converting data set |
|
| 135:57 | away of datasets over here? One the most of our converter wave energy |
|
| 136:05 | our horizontal components uh receiver. Most that is coming from conversion upon reflection |
|
| 136:14 | transmission. So we have here a . Is this true or false? |
|
| 136:23 | angles of the outgoing ways are determined Snell's law through the equality of the |
|
| 136:30 | velocity in all these different modes. Stephanie, is that true or |
|
| 136:37 | The statement is true but the equation wrong. So false. Okay, |
|
| 136:42 | uh yes, the statement is true uh equation is false because actually we |
|
| 136:53 | the same horizontal slowness in all So very good. That was a |
|
| 136:58 | question. Now um is this true false the exact plane of my reflection |
|
| 137:07 | can be written in terms of these non dimensional qualities. So the density |
|
| 137:19 | , isn't it supposed to be P over P. One and then the |
|
| 137:23 | for the last term has to be 12. So it's false. No |
|
| 137:27 | it's not true. It's different than I showed you. But we can |
|
| 137:32 | this normalization in lots of different And so so this is one. |
|
| 137:37 | we have to do is we have end up with three non dimensional velocities |
|
| 137:43 | one non dimensional density. So uh this will do it different from what |
|
| 137:49 | did before. Maybe in some cases might be better because this cheer wave |
|
| 137:55 | ratio here is a p wave velocity . And so then here is a |
|
| 138:02 | . P V. S velocity ratio the upper meeting. So this would |
|
| 138:05 | work okay for false. Since all terms and the expressions for the exact |
|
| 138:12 | wave reflection cards are real. The itself is really to a far uh |
|
| 138:22 | it's not true because the predicate here uh is false. It's not true |
|
| 138:29 | in general that all of the terms real. I just show you post |
|
| 138:34 | reflection um uh some of those times not real. So that means that |
|
| 138:40 | itself is not real in all in the general case. So uh |
|
| 138:50 | complexity is hidden within the notation. that's why it looks like it should |
|
| 138:55 | real. But if you go back our discussion of post critical angles, |
|
| 139:01 | see those uh, those post critical of those post critical angles are appearing |
|
| 139:07 | this expression that we looked at those are imaginary, then coefficient itself is |
|
| 139:14 | to be complex. So go back check the, check the equations |
|
| 139:22 | I'm gonna ask you to do a bit of mental arithmetic. So let's |
|
| 139:28 | a case at a sediment salt The incident wave is coming in with |
|
| 139:35 | , which is not uh not uh of typical for p wave velocities in |
|
| 139:43 | . Made a round number here, kilometers a second. And inside the |
|
| 139:48 | , it's a lot faster. So for easier, I think I'm gonna |
|
| 139:52 | it for uh kilometers. Uh remember formula for the critical angle and |
|
| 140:04 | yes. Which of these answers is best answer. Three degrees. I |
|
| 140:13 | hear it 30 30 degrees, Because the sine of 30 degrees is |
|
| 140:19 | half. Which is this ratio So this is wrong on its face |
|
| 140:24 | that's not an angle, that's the . So, uh 30 degrees. |
|
| 140:27 | that's pretty small angle. Um uh , uh, let's not jump to |
|
| 140:37 | conclusion that all of our data has be less than period degrees because this |
|
| 140:42 | an unusual interface. Most of our don't have uh, this big difference |
|
| 140:49 | and uh so uh furthermore uh sediments interface, you've got to consider that |
|
| 140:59 | , the incident velocity might be bigger this and the velocity in assault might |
|
| 141:05 | less than this. So, uh is not a hard limit here, |
|
| 141:13 | even in the case of a sediment interface. But it shows that it's |
|
| 141:18 | you need to worry about. If have, if you're looking at data |
|
| 141:22 | there's a salt body down there, might be that some of those uh |
|
| 141:28 | angles are most critical. Yeah, us now go on to um the |
|
| 141:39 | , which is uh one that we um think about more deeply. So |
|
| 141:49 | previous results were exact but they're almost for us because real walks are usually |
|
| 141:54 | exactly ice and tropic, as we to make that reasonable and Real walks |
|
| 142:01 | not exactly elastic either. As we to make that result, real interfaces |
|
| 142:07 | usually not planer and incident waves are curved. So that's potentially a problem |
|
| 142:14 | us. Not included in the So called exact analysis and real face |
|
| 142:20 | are not isolated from each other but close to other interfaces. So the |
|
| 142:25 | , let's are interfering the wave reflected the bottom interface is going to be |
|
| 142:32 | in just a little bit after the look reflected from the upper interface. |
|
| 142:37 | two letters are gonna interfere with each and make problems unless we deal with |
|
| 142:44 | . And here is the main reason we don't use those um equations is |
|
| 142:50 | can't get our minds around. They're too complicated. So what we're gonna |
|
| 142:55 | is find an appropriate approximation. most often the appropriate approximation is the |
|
| 143:03 | between the upper medium and lower medium elastic contracts. Furthermore, we're gonna |
|
| 143:11 | that the incident angle is not so that we have to worry about the |
|
| 143:15 | critical angle that we deal with that . And for now we're going to |
|
| 143:21 | that the media are actually profit perfectly and well separated from other interface. |
|
| 143:27 | these limiting assumptions, the crucial one actually this one right here. That's |
|
| 143:32 | make a big difference for us. notice that we never measure reflectivity as |
|
| 143:41 | function of angle. Never ever. we measure received amplitudes as functions of |
|
| 143:49 | . So we have to convert what receive into uh idea into other quantities |
|
| 143:58 | are suitable for analyzing using the reflectivity . So, our first challenge is |
|
| 144:07 | convert offsets to incident angle. What means is we're going to need to |
|
| 144:13 | what is the velocity field in the overburden above. The reflect is not |
|
| 144:19 | be uniforms. So the rays are going to be straight in the |
|
| 144:23 | They're gonna be curving down through the following Snell's law and they're gonna hit |
|
| 144:29 | uh we're gonna hit them reflector at angle that we don't know uh without |
|
| 144:36 | the calculation and how do we do ? Well, we trace rays through |
|
| 144:40 | velocity model to determine what incident angle to what sources say was. So |
|
| 144:50 | this convolutional convolutional description of wave Most of these items in here make |
|
| 145:00 | dependent uh variation of the amplitude. let me quiz you on this. |
|
| 145:08 | Stephanie, let's start at the start over here. And uh so |
|
| 145:14 | is the source of strength? It here, it's a function of |
|
| 145:23 | Uh Why is that? So give a couple of real world reasons why |
|
| 145:31 | source strength is gonna be a function angle from your comments. Mm I |
|
| 145:44 | know. Um Well okay so let turn to Utah Utah give us an |
|
| 145:57 | of something we do to make an dependent source. Yeah, that's a |
|
| 146:12 | one. So on land we're gonna vibrating uh the ground, we don't |
|
| 146:18 | dynamite much anymore on land and we by the way when I was |
|
| 146:23 | Standard practice. But now we use . And so normally we use vertical |
|
| 146:31 | . And the reason for that is want to concentrate the uh the p |
|
| 146:36 | coming off that vibrator are gonna have attitude near vertical. Of course you're |
|
| 146:42 | have some attitude at oblique angles. of course they're also gonna be generating |
|
| 146:48 | waves but uh we designed them vertically maximize the um the amplitude and vertical |
|
| 146:58 | near vertical direction. But there is variation. And as you go from |
|
| 147:03 | oblique to horizontal, it has to less and less amplitude in the, |
|
| 147:09 | the outgoing waves from, from a . So Utah give me a marine |
|
| 147:25 | advice the so I'm I'm having a time Utah hearing you because of audio |
|
| 147:53 | I think on your end. So me take up the, the idea |
|
| 147:58 | you have an air gun towed behind uh, the acquisition vessel. And |
|
| 148:06 | and we normally, we normally have than 11 air gun. We have |
|
| 148:10 | array of air guns, uh maybe dozen of them uh in an |
|
| 148:14 | And the, the uh the geometry the array is designed. So that |
|
| 148:19 | the timing of these different air guns designed to maximize the p wave um |
|
| 148:27 | amplitude in the vertical direction, near directions. And so there again the |
|
| 148:33 | function is going to be a function takeoff angle. Now there's another effect |
|
| 148:39 | , some of the energy from this gun array goes down and some of |
|
| 148:45 | goes up towards the surface. It off the uh, off the surface |
|
| 148:51 | comes back down again with a little following the direct uh waves downwards. |
|
| 149:00 | so the amount of the delay depends um uh take off angle from the |
|
| 149:07 | . So if it's, it's truly , you get one delay. And |
|
| 149:12 | it's let's say uh 20 degrees uh you're following a 20 degree rate upwards |
|
| 149:18 | then downwards that delay is going to a little bit longer. So the |
|
| 149:23 | between the uh red wave and uh so called source ghost which comes from |
|
| 149:32 | reflection off the surface. That's that interference is going to be angle |
|
| 149:38 | for that reason. So there's another of how we have angle dependent |
|
| 149:44 | So uh uh Wavell, it might angle dependent but let's ignore that. |
|
| 149:53 | the downward propagation operator, there's a of complicated stuff hidden inside here. |
|
| 150:02 | Stephanie, tell me why this uh propagation and see we haven't even gotten |
|
| 150:07 | the reflector yet, we're propagating downwards as the wave goes downwards uh is |
|
| 150:16 | amplitude changing as a function of ray or is it the same for |
|
| 150:24 | You know, it's going to be off with different uh amplitudes because of |
|
| 150:28 | source here. Um but as it down, is changing amplitude further um |
|
| 150:37 | a function of angle, What are effects in this um propagation? Um |
|
| 150:48 | which which could modify the uh And for two, as a function |
|
| 150:55 | angle Stephanie you can probably think of couple, I mean, wouldn't the |
|
| 151:03 | be like decreasing? Yeah of course will be decreasing. Uh from geometrical |
|
| 151:11 | and also decreasing from attenuation and that's be um that's going to be um |
|
| 151:21 | of those are gonna be dependent upon length. And so uh forgiven um |
|
| 151:28 | receiver offset, the path links are be longer for the old lee um |
|
| 151:34 | than for the um normal incidence. , naturally because of those effects that |
|
| 151:42 | amplitude over here is going to depend offset because of this. What's happening |
|
| 151:51 | ? No, not what's happening I mean in addition to what's happening |
|
| 151:55 | . So uh Utah, can you me another example of an effect happening |
|
| 152:01 | this propagation downwards which affects the amplitude a function of angle, I would |
|
| 152:18 | because of the 39. So the unusual from bird at a same |
|
| 152:26 | increase the image. That's right, right, that's over in a in |
|
| 152:31 | real case, the overburden is never . So what that means is that |
|
| 152:37 | going to be at every uh interface the one we're interested in, there's |
|
| 152:44 | be a transmission coffee. And so transition carp fishing is going to vary |
|
| 152:48 | a a a. Yeah, so then what what as a result |
|
| 153:02 | these and similar things for everyone? can you mute your things. Thank |
|
| 153:21 | . Okay, so um uh what just learned is that inside this propagation |
|
| 153:29 | , there's a lot of uh amplitude with offset which has nothing to do |
|
| 153:35 | the reflectivity. So that's in our . So we gotta keep that in |
|
| 153:40 | . So uh uh furthermore, uh some processing which is happening here, |
|
| 153:49 | what this is about and so um very common. So what uh if |
|
| 154:00 | an interpretation geophysicist, you're gonna be at data which has been uh previously |
|
| 154:08 | on by somebody else in the processing and uh they might have affected the |
|
| 154:15 | also. So uh when they make image, uh you know when you |
|
| 154:22 | an image all the amplitude information is , but but if you make a |
|
| 154:29 | image gather, so you you uh all the different offsets, uh getting |
|
| 154:38 | to stack them together to make a image. That comment image gather has |
|
| 154:47 | an offset variation uh which might have affected by whoever did the processing. |
|
| 154:55 | uh these days he's gonna be he's be doing his best to make two |
|
| 155:00 | preservation during the construction of this common gathered. But uh that impact he |
|
| 155:12 | on the amplitudes is gonna depend in crucial way on how well he's able |
|
| 155:17 | pre to preserve the amplitudes. And it's gonna be different for every imaging |
|
| 155:29 | . And so I'm not gonna talk further here. But uh what I |
|
| 155:34 | conclude is that if you're in charge an HBO project and they give you |
|
| 155:40 | data, uh you need to talk the imaging experts to uh understand what |
|
| 155:49 | think they have done in the computer uh these amplitudes. So that apparent |
|
| 156:00 | effect may or may not be something , it might be a artifact, |
|
| 156:07 | only propagation effects in the overburden but processing effect in the processing. So |
|
| 156:15 | learned today. Now most of us commercial software for analyzing amplitudes. Maybe |
|
| 156:26 | uh provided by Hampton Russell, Maybe provided by food grow, maybe you |
|
| 156:32 | your in house stuff. Uh So each of these uh software packages uh |
|
| 156:40 | a set of procedures, usually including . And these procedures are designed to |
|
| 156:47 | for many of the propagation effects that talked about so that the resulting normalized |
|
| 156:53 | give the reflection coefficient as a function . So they're trying to do is |
|
| 157:00 | rid of all this stuff so that yield this reflection coefficient as a |
|
| 157:07 | These procedures are usually oversimplified, just criticize those people uh without giving any |
|
| 157:16 | uh saying it's oversimplified. But even , I'm going to assume for the |
|
| 157:22 | they are adequate for the purpose, shortcomings they have. Uh Let's not |
|
| 157:28 | about that yet. So here is the exact expression without all the |
|
| 157:36 | So, I left room down here uh removing all the notation. Um |
|
| 157:43 | is the same formula, the exact which you can find in Aachen Rich |
|
| 157:49 | we're gonna reformulate it exactly in in terms here, we're gonna uh get |
|
| 157:56 | non dimensional density by defining the density provided by the averages and similarly for |
|
| 158:06 | and for Gs. And then we're find uh gonna have this this average |
|
| 158:13 | ratio. So three non dimensional velocities one non dimensional density and it's just |
|
| 158:22 | bunch of algebra to put these to um this expression into where the before |
|
| 158:35 | parameters are. Not those defined by richards, you know, VP one |
|
| 158:40 | VP two and so on. These non dimensional, that's just a bunch |
|
| 158:44 | algebra. And then we're going to the case of weak classic contrast by |
|
| 158:50 | that these fractional differences. Yeah, have three fractional differences, density, |
|
| 158:58 | P and V. S are all than one, a lot smaller. |
|
| 159:04 | then we uh thank you. Taylor of uh this expression and we assume |
|
| 159:15 | all the terms in the taylor expansion have these differences to more to the |
|
| 159:21 | power than one. Those are So we're gonna end up in uh |
|
| 159:25 | a simple expression only the first um first power of these three quantities. |
|
| 159:36 | that's this, I think you can that that's really made a substantial |
|
| 159:43 | So we have uh simple, simple and we have all the material complexity |
|
| 159:52 | uh inside these core functions which are by these expressions here. So let's |
|
| 159:59 | at the first one until these are or two in our first this is |
|
| 160:03 | normal incidence reflection. This is exactly we determine previously today. And then |
|
| 160:11 | got a gradient turn which is our hear that appears here, it multiplies |
|
| 160:21 | sign dependence uh science, great dependence their here. Now look how this |
|
| 160:26 | a range for for zero angle of . These two terms go away and |
|
| 160:32 | left with this one for small This is a small non zero |
|
| 160:37 | And see this is even smaller because assuming that the sine squared of theta |
|
| 160:42 | small. That means the tangent squared theta is also small. So we |
|
| 160:46 | neglect this at normal incidents are at angles and that's a clever thing to |
|
| 160:52 | it like this. And so this is given by this and you see |
|
| 160:57 | it's got in there, not only jump in VP, but also the |
|
| 161:01 | in density, jump in share jump in density or shooting inside |
|
| 161:08 | jumping density is appearing in the gradient jump in Sure. Model is given |
|
| 161:16 | ingredients jump in VP itself is given here and in the current term. |
|
| 161:23 | this is different from this one because one contains the density as well. |
|
| 161:30 | to get here, we also use two uh relations from general calculus, |
|
| 161:38 | in Z jump in Z P is to jump in and VP. And |
|
| 161:44 | plus the jump in density, all are normalized that you show here and |
|
| 161:50 | the jump in mu is given in of the jump nvs and density like |
|
| 161:57 | , and you of course you're going recognize that this jump in uh VP |
|
| 162:04 | given explicitly right here. That's that's jump in VP. And here's the |
|
| 162:09 | value of V. P. So now this is a foreigner we can |
|
| 162:24 | with. This is simple enough for to uh to understand. Uh And |
|
| 162:29 | is in fact the standard way of at at Avio amplitudes in terms of |
|
| 162:36 | simplified expression for um reflecting. But other ways to do it. For |
|
| 162:45 | , you might be you might uh somewhere the reflectivity grading is given in |
|
| 162:54 | of physical properties like this, where is now the jump in Parsons ratio |
|
| 163:00 | Parsons ratio is non dimensional. So don't have to divide by average Parsons |
|
| 163:07 | in parcels ratio followed by this complicated here involving junction Parsons ratio and jumps |
|
| 163:14 | density. It also involves the average ratio here here. So now this |
|
| 163:23 | uh quite simple if we have average ratio is 1/3. All the thing |
|
| 163:30 | away. So the second part of is right. This is quite |
|
| 163:34 | but that's commonly not true in all of rocks. For example, if |
|
| 163:39 | velocity ratio of the average velocity ratio a number like three. And this |
|
| 163:44 | typical of shallow marine sediments. Yesterday talked uh Stephanie's elected number two for |
|
| 163:51 | . You can uh again, uh that's again for yourself, what happens |
|
| 164:01 | the velocity ratio is two? What you get gonna get for the approximate |
|
| 164:06 | ? It's going to be different from but it's not gonna be one |
|
| 164:10 | This is a more typical number for marine sediments. And in that case |
|
| 164:15 | expression this term does not go away the results of this, which is |
|
| 164:23 | um find this term with this And you get this which is arguably |
|
| 164:34 | no more simple. And the straight uh statement from right here, we're |
|
| 164:43 | talk about it in these terms. I want to show you one more |
|
| 164:47 | that you might see in lecture. might see the great intern given in |
|
| 164:52 | of the jumps in the LeMay I'm going to claim that again, |
|
| 164:58 | is more complicated than the first phone lectures. So now using that um |
|
| 165:10 | Previous expressions for intercept great encouragement, can find these um jobs directly here |
|
| 165:21 | jump in VP jumping, rope jumping . S. In terms of the |
|
| 165:27 | and the intercept and the grading We use these these terms here to |
|
| 165:38 | this. And in some cases you , well this is what we really |
|
| 165:44 | . You really want these jobs in parts. So it looks easy, |
|
| 165:49 | it's difficult in practice because of the here are those same three relationships. |
|
| 165:56 | this is the one we probably want know most the jump in VP but |
|
| 166:00 | curvature is usually the worst determined of of the Avio activist, usually this |
|
| 166:09 | current return is very poorly determined. that's bad what we want. It |
|
| 166:15 | upon what we, what we have confidence. Best determined uh of these |
|
| 166:23 | parameters is innocent and it's frequently not ours, but usually impossible to |
|
| 166:31 | the grating. Yeah, be absolutely honest with you. We don't really |
|
| 166:42 | these three observables. And why is ? It's because the seismic trace has |
|
| 166:47 | unknown scale factor. Usually somebody before ever see the day that some traces |
|
| 166:54 | have been re scaled to lie somewhere plus or -1000. So if you're |
|
| 167:01 | on your workstation and you're looking at seismic session, you put your mouth |
|
| 167:05 | not a seismic section on seismic You put your mouse over any |
|
| 167:10 | And uh it's gonna come back with number probably between plus or minus |
|
| 167:16 | But reflect activities usually are much Four orders of magnitude smaller. So |
|
| 167:23 | we can determine our certain ratios such the ratio of the gradient to the |
|
| 167:28 | . In that case the unknown scale cancels out. So this is uh |
|
| 167:34 | is the number that we can And with great uncertainty, we can |
|
| 167:42 | the non dimensional uh curvature. But of the uncertainties, you rarely see |
|
| 167:49 | analyzing this. So we usually have one reliable seismic amplitude attribute which is |
|
| 168:07 | relative value of the intercept. Before we should go any further or |
|
| 168:16 | should recognize that that we don't really to find physical properties. What we |
|
| 168:21 | want to find is highly. So not get um let's not get overly |
|
| 168:31 | . Um Finding these property jumps what we want to find is |
|
| 168:37 | And so we know that hydrocarbons are common in the subsurface, there are |
|
| 168:42 | . So let's use a V. . To find these anomalies. So |
|
| 168:51 | consider only the intercept and ingredients. here's the intercept the agreement and we're |
|
| 168:55 | do it for these two occasions. sedimentary interfaces where there's brian on both |
|
| 169:02 | of the interface. That's the normal . That's going to be happening in |
|
| 169:07 | all reflect that you see are gonna reflections off of brian brian interface. |
|
| 169:14 | some of them are going to have carton on one side of the |
|
| 169:18 | Let's look at the uh special case there's gas on the other side because |
|
| 169:23 | is really a lot different from brian the physics department. And so normal |
|
| 169:32 | interface, here's our two expressions for ingredients and based on laboratory data art |
|
| 169:43 | a bunch of rocks and measure their . P and V. S and |
|
| 169:48 | the in their density and reduce the modules. And normally and then pick |
|
| 169:53 | of those at random. And normally gonna find that this uh this difference |
|
| 170:00 | here, it's so big that the term dominates the first. So that |
|
| 170:06 | that the ingredient has the same algebraic as the second term and that means |
|
| 170:13 | has the opposite uh algebraic sign on intercept because of this minus sign. |
|
| 170:21 | reading has algebra sign opposite to that's the normal text. But for |
|
| 170:30 | grind gas energies Looking at the same equations, this term is gonna be |
|
| 170:36 | and we're going to learn about that from in lesson eight. You see |
|
| 170:43 | again, if it's the same mythology both sides of the interface, um |
|
| 170:50 | this term is gonna consider dominating. term is gonna be zero. So |
|
| 170:54 | algebraic sign of the ingredient is gonna the same as this, which is |
|
| 171:00 | be the same as this. So such interfaces the algebraic sign has the |
|
| 171:08 | , it is the same for the and the interest and the real world |
|
| 171:14 | be complicated. For example, there be a little ology difference as well |
|
| 171:18 | a different across property. Yeah. . Well let me show you uh |
|
| 171:35 | software with a particular example. This software from BP. And this is |
|
| 171:41 | this is not Bp secrets. It's published uh and uh my friend did |
|
| 171:48 | analysis and what what this is a D. Analysis. And so what |
|
| 171:53 | see here is uh two D. section so that it's an image and |
|
| 172:01 | never mind how they made an But you know that behind every one |
|
| 172:05 | these image points there lies a gathered midpoint gather. Common image point gather |
|
| 172:12 | this is all pretty flat line. these common midpoint gathers, uh pretty |
|
| 172:18 | approximations to common image gather and um that's not showing you what you see |
|
| 172:29 | the result um some flattening those gatherers summing them up to make uh point |
|
| 172:38 | the image. Remember that every point this image has behind it again. |
|
| 172:44 | so when the interpreter first brings this , you don't see any colors here |
|
| 172:48 | this is blank. And all you is is the uh oh is the |
|
| 172:58 | ? And let's look over here and what we have. This is a |
|
| 173:01 | plot where we have the uh the and the great on this cross |
|
| 173:07 | And when he first brings this up all black. So then what he |
|
| 173:11 | does is he notices, wow, at this attitude anomaly right here in |
|
| 173:15 | middle. Uh is that gonna is that due to hydrocarbons or is |
|
| 173:22 | due to something else? Some length anomaly in the service? We're gonna |
|
| 173:28 | to find that out. So the thing he does is he draws uh |
|
| 173:32 | box around the anomaly. And as as he completes the yellow box |
|
| 173:38 | every point interior to the yellow box lights up over here, all these |
|
| 173:44 | are yellow and these points here on cross line, give that intercept. |
|
| 173:51 | the gradient lying behind every one of points inside the yellow box and you |
|
| 173:57 | see it's a diffuse cloud of yellow . So the next thing the interpreter |
|
| 174:10 | is he draws an interior green doesn't matter what the shape is, |
|
| 174:16 | according to his expert, um there are no hydrocarbons inside here. |
|
| 174:23 | all of these, all of these here are simply brian brian interfaces caused |
|
| 174:30 | um uh with a logic contrast across boundaries. And he could have gone |
|
| 174:36 | also, he just chose this and soon as he completes this yellow |
|
| 174:40 | this green box, some of these here turned green. These are |
|
| 174:46 | these are not still yellow and but got some green points here and notice |
|
| 174:51 | the green points form a tight cloud the middle of this diffuse cloud and |
|
| 174:58 | has this orientation, it's an elongated uh in the Yeah, second quadrant |
|
| 175:09 | the fourth part. Remember how, you used to name these in |
|
| 175:13 | So this is this is the first or both of these things are positive |
|
| 175:18 | and by the way, why not is zero, this is the |
|
| 175:21 | So all these are positive here. are positive here. Over here, |
|
| 175:26 | intercept is uh negative over here both negative and over here the ingredient is |
|
| 175:34 | . So this is order 123 and and literal. Odjick um plowed always |
|
| 175:42 | oriented like some and then he notices the interpreter notices that uh he's got |
|
| 175:51 | bunch of yellow points outside here and here. Uh and these are these |
|
| 175:58 | contain hydrocarbons. It guarantees that these points have no hardcovers. And hear |
|
| 176:07 | often this has a negative slope to tight elongated clown. Now he uh |
|
| 176:16 | works so now what he does is he's gonna select on the cross plan |
|
| 176:23 | points here. And as soon as completes, as soon as he selects |
|
| 176:28 | on the cross plot, the corresponding show up over here. Now, |
|
| 176:34 | is the important part because if these these uh these were these points were |
|
| 176:40 | . Now he's uh selected them. now they're purple. If those things |
|
| 176:45 | from all over here, it would be noise. But you see, |
|
| 176:49 | don't come from all over there, from the top of the structure. |
|
| 176:54 | there's a pattern there. And that's and he immediately suspects that these points |
|
| 177:06 | the top of the structure um correspond anomalous fluids, i. E. |
|
| 177:17 | . And how do we know they're ? We don't know that until we |
|
| 177:21 | at the cross plant. And so have a vo characteristics uh with negative |
|
| 177:32 | , intercept and negative uh negative intercept negative grading. Yeah, he was |
|
| 177:43 | by a simple minded theory that says these terms are all in the third |
|
| 177:48 | should be um uh I think it's a Class three anomaly. Not |
|
| 177:54 | Somebody made a classification, but look , we got uh these are probably |
|
| 177:59 | same anomaly here. Uh Nature doesn't like classifications. It's uh has smooth |
|
| 178:06 | and so these are probably the same . And this is probably the |
|
| 178:11 | the bottom of the anomaly. It's those, but these are more interesting |
|
| 178:15 | the bottom is flat and the top uh structure. So um by the |
|
| 178:26 | , I don't know whether this is time series or gets here, I |
|
| 178:32 | know that uh similar results or time . That's So what we've done is |
|
| 178:44 | found that the anomalous points in the plot correspond to the top of the |
|
| 178:49 | in real space. So we've been by and by the way, this |
|
| 178:54 | exactly what we uh decided back Uh we took this miniaturized expression for |
|
| 179:07 | reflectivity um or efficient. And then applied reasoning to those reflectivity curves and |
|
| 179:17 | found out that if there's a if comes from a a brine gas |
|
| 179:23 | yeah, yeah, reflectivity should have same physical sign. Uh So the |
|
| 179:31 | and the intersect and that's what we found right here. Same algebraic sign |
|
| 179:38 | the intercept and the gradient. And analyzing the reflectivity, that's what we |
|
| 179:45 | . But this is data. right. Who knows what um uh |
|
| 179:54 | other effects might be here. These received amplitudes. These are not |
|
| 179:59 | These are if you look at every of these uh it's a big |
|
| 180:05 | See the intercept here as dimensions that up to 5000 here and -5000 |
|
| 180:12 | So these are big numbers. It be uh reflectivity is, this is |
|
| 180:19 | data but guided by the period for ease. We have uh been able |
|
| 180:26 | empirically locate on harmless shows in the . So this is uh not a |
|
| 180:34 | conclusion but it does substantially lower the . So we call this the qualitative |
|
| 180:41 | your program often works even though there many cases which uh don't correspond to |
|
| 180:49 | kind of analysis and those always puzzled . Uh so let me pause at |
|
| 180:58 | point and tell you the following Um um so this analysis I gave |
|
| 181:09 | was from D. P. Uh was uh those grassroots published and the |
|
| 181:18 | part of the 21st century after repeat America. Well um uh they come |
|
| 181:30 | from chemical analysis. Sin was Emma heritage guy. I was an and |
|
| 181:38 | fact I am the the inventor area . So that's an interesting story which |
|
| 181:49 | will now tell you. So I Amoco in um she in 1980, |
|
| 182:01 | when I joined aven and I joined in the rock physics department in the |
|
| 182:07 | physics section of the geophysics department of research center in Tulsa. So the |
|
| 182:16 | department was in the Houston and new and Denver and uh and regional offices |
|
| 182:24 | . Research center was impulse. So joined um chemical at a time when |
|
| 182:35 | uh well business was moving and um there are lots of small oil companies |
|
| 182:45 | are hiring hiring experienced people away from major oil companies by offering them larger |
|
| 182:55 | often including royalty. So if you're experienced guy working for Amoco you get |
|
| 182:59 | offer from uh from a small company and they say well we're going to |
|
| 183:04 | your salary by 50%. And if you make successful recommendations on where |
|
| 183:10 | are grill you're gonna get like a of the disk of that discovery. |
|
| 183:18 | that can, that can be pretty money. You could get rich by |
|
| 183:24 | a good geophysicist. Whereas uh continue work for a big work on being |
|
| 183:30 | hammock, oh you're gonna be comfortable you're not gonna be rich. So |
|
| 183:36 | were hiring away the experienced people and the major companies were replacing the experienced |
|
| 183:43 | with new hires and so they would recruiters to the universities like and all |
|
| 183:49 | universities in the, in the oil , which is what we call the |
|
| 183:54 | , Oklahoma and lucy and museum. those universities uh getting regular visits from |
|
| 184:03 | recruiters from the major oil companies and up the graduating seniors as fast as |
|
| 184:09 | could. That's right. And that enough. So they started expanding their |
|
| 184:17 | activities eventually they got as far north new york where I was teaching in |
|
| 184:21 | state University of new york and I teaching of course uh curiosity and uh |
|
| 184:31 | birth of deep interior of the earth earthquakes. So that's what I was |
|
| 184:38 | . And also the rock properties of very deep rocks. They got up |
|
| 184:45 | my university and they liked the quality the graduates that they were producing and |
|
| 184:50 | they would hire some and then next they would come back with those same |
|
| 184:57 | new hires in tow now with one experience and they would make friendly greetings |
|
| 185:03 | all their friends who are not yet . And and they would give a |
|
| 185:10 | showing all the exciting stuff they've been at the oil company in the previous |
|
| 185:17 | . And I'm sitting there in the thinking, you know, uh why |
|
| 185:22 | these kids have all the fun? I could do that. So |
|
| 185:26 | when the recruiter uh I said okay who wants to join us? Uh |
|
| 185:33 | year I held up my hand and they said, oh well we hadn't |
|
| 185:38 | about how in faculty, but let's . And so we did talk and |
|
| 185:42 | I got an offer to join Amoco's Center in Tulsa, roughly double my |
|
| 185:50 | salary. So uh my wife and had to decide whether we wanted to |
|
| 185:57 | this or not at this time. was also working as a staff member |
|
| 186:01 | the university and she was actually much famous at that time than I |
|
| 186:07 | She was uh she was the premed premed adviser and she was exceptional. |
|
| 186:16 | was amazing at getting and graduating premed into medical school and she was famous |
|
| 186:26 | over the Northeast for her success. in fact she was the President elect |
|
| 186:32 | the Society of Premed advisers there for Northeast. And the university was so |
|
| 186:38 | of her work. They were advertising the high school seniors come to come |
|
| 186:44 | new york, we will get you medical school, you don't have to |
|
| 186:49 | your family's money at a private school Columbia. And that was really working |
|
| 186:55 | that was the only accepted in those the top 7% of the students from |
|
| 187:01 | high schools in New York. So you had to be a straight a |
|
| 187:04 | to get into the State University State University of New York at |
|
| 187:11 | It was all the public I've been school were good and those are the |
|
| 187:17 | of graduates we were producing for the companies from the geology department. Now |
|
| 187:23 | had this offer to join um ethically Tulsa or not. And it was |
|
| 187:30 | problem because she was not famous. wife was not famous in Oklahoma. |
|
| 187:35 | was famous in the Northeast and I know anything at all about the oil |
|
| 187:41 | . What I knew about was deep furthermore, I had a tenured |
|
| 187:48 | I had a lifetime job um at in New York. And what America |
|
| 187:55 | offering me was a 30 day But we decided that we would give |
|
| 187:59 | a try. And so we went Tulsa and um um one of the |
|
| 188:06 | things that happened one we had an office in New Orleans and then and |
|
| 188:19 | we were exploring in the gulf of . Uh we're partners with mobile on |
|
| 188:30 | certain play in the gulf of So you've got to understand that an |
|
| 188:34 | company, it has various temporary partnerships various other oil companies uh with respect |
|
| 188:42 | certain specific um prospects. So at time a major oil company like chemical |
|
| 188:51 | be involved in a dozen or two partnerships with other oil companies. Each |
|
| 188:58 | focused on a certain area. In case we were focused on a certain |
|
| 189:03 | in the gulf of Mexico. Uh uh only partner was mobile and in |
|
| 189:11 | partnership like this, one of the is designated as operating partner. And |
|
| 189:16 | others are support partners. So we the only support partner in this hall |
|
| 189:23 | . They were the operating and so a certain required some data and in |
|
| 189:30 | days oil companies did most of the in house. So at a certain |
|
| 189:35 | in the processing mobile guy calls up Amoco partner says, hey ralph come |
|
| 189:43 | over. I want you to look our our processing on this prospect. |
|
| 189:52 | the Amoco guy, they set a and time the american guy walks down |
|
| 189:56 | street in new Orleans and they reach other. You know their friends, |
|
| 190:00 | been colleagues for a long time, have a cup of coffee, they |
|
| 190:03 | some gossip. And then the mobile rolls out on the table uh two |
|
| 190:09 | . Cross section uh printed on paper those days and probably in color color |
|
| 190:19 | advance party from black and white to . And he rolls it out and |
|
| 190:24 | says this is where we are so in the process. And um uh |
|
| 190:33 | look at it and uh this is the first time they've seen an image |
|
| 190:39 | this. Uh This is a better they've seen before because processing department has |
|
| 190:44 | working and refining velocities and so So they have a pretty good |
|
| 190:49 | And then the the beef. Then mobile guy takes a second uh paper |
|
| 190:57 | it out on top of the first is this is the Monet diagram for |
|
| 191:01 | Monet plot showing the shear wave problem it's got a lot of different colors |
|
| 191:08 | it. But the Amoco guy's jaw because he knows this is a marine |
|
| 191:13 | , they are not receiving any share arrivals. And so he's amazed that |
|
| 191:19 | has this uh shear wave section. guy sees on the Amoco face surprised |
|
| 191:27 | he realizes that by mistake he has some proprietary mobile technology which he should |
|
| 191:35 | have shown to this amicable. They the operators, they have no obligation |
|
| 191:41 | show the results of proprietary systems. this? So he makes a |
|
| 191:50 | He says, oh, this must something else. He rolls it out |
|
| 191:53 | puts it away, must be some of mistake. And they go on |
|
| 191:56 | the meeting following the standard agenda. the MMO guy knows that he has |
|
| 192:03 | something that's dynamite. So as soon he gets out of the meeting, |
|
| 192:06 | runs back to the office, tells boss, those guys at mobile, |
|
| 192:11 | know how to uh huh they know to get sharing properties in a marine |
|
| 192:19 | , wow. So uh, that's in the day and so 8:00 the |
|
| 192:24 | morning, my boss has fallen up Tulsa brains and the project gets assigned |
|
| 192:31 | me because I'm new in the Everybody else has their plateful of other |
|
| 192:36 | . Uh, and they were supposed make progress on those projects. My |
|
| 192:41 | is not yet full because I'm new the house. That comes to |
|
| 192:44 | So very quickly I uh, figured , I think one of the things |
|
| 192:49 | I did was I went to high richards and uh, it's right there |
|
| 192:53 | , spelled out in terms which are too different than what I've showed here |
|
| 192:59 | without the hydrocarbon, um, which we talked about just half an |
|
| 193:09 | because arcane richards were deep Earth curiosity driven, not utility driven. |
|
| 193:16 | so they didn't know or care much the oil business but they had most |
|
| 193:20 | the analysis that I showed you So I very quickly I realized the |
|
| 193:27 | argument that I just showed you in last um half pounds. I didn't |
|
| 193:35 | the software example of course much months and we didn't even have the word |
|
| 193:42 | . B. O. In those we had a different name for this |
|
| 193:47 | inside. Mm but we realized that we uh analyze our amplitudes as a |
|
| 193:56 | offset, maybe it gives a clue to what's down there. In |
|
| 194:02 | so we can do better than making image. We can tell you something |
|
| 194:06 | the physical characteristics of what's down there particular. Maybe we can tell you |
|
| 194:11 | or not hydra apartments are really there you see an anti client in the |
|
| 194:16 | service image, you know that um hydro counts might be there. That's |
|
| 194:24 | detection of hydrocarbons. This was potentially detection of amplitudes by looking at |
|
| 194:35 | direct detection of heart departments by looking the amplitudes as they vary with officer |
|
| 194:42 | dynamite. So immediately what Amoco did they scrambled the team of experts and |
|
| 194:47 | went down to new Orleans and they an office off site from the |
|
| 194:53 | they're in a warehouse somewhere. They close and they got a bunch of |
|
| 195:01 | and medical data for they had previously required in the gulf of Mexico and |
|
| 195:06 | had drilling results from those episodes and were successes and some are not. |
|
| 195:13 | so now we look at the data lay behind those drilling operations and we |
|
| 195:21 | that that uh where the drilling had discovery of harder conference, the corresponding |
|
| 195:30 | data had what we now call positive in it. We hadn't known previously |
|
| 195:36 | look for it. Now we did we saw immediately that if we only |
|
| 195:42 | wells which have positive Avio will have better success, It will be 100% |
|
| 195:48 | it's much better success rate. So , this uh analysis with a secret |
|
| 195:58 | offsite in your on that was accomplished just a few weeks and we realized |
|
| 196:05 | we now have a way to do action and higher departments before drilling from |
|
| 196:11 | data. Not foolproof but really useful . And so immediately then the project |
|
| 196:22 | in Tulsa was taken away from me I was in new hire and uh |
|
| 196:28 | important new development like this couldn't possibly left in the hands of a new |
|
| 196:34 | . So they gave to one of old guys, cancel him out of |
|
| 196:40 | previous projects, gave him this So, um as a result, |
|
| 196:46 | didn't make any more progress in the for the next 30 years. There |
|
| 196:54 | a problem which I saw even in days, which is clearly indicated in |
|
| 197:01 | example that we're looking at there is problem. Um Let's look at bubble |
|
| 197:09 | trend here, We have a tight and we have no hydrocarbons anywhere inside |
|
| 197:15 | green box, but the slope is steep. Something is wrong. |
|
| 197:22 | remember that. This is received amplitudes . This is got in it. |
|
| 197:27 | of the effects of propagation and everything in there in these amplitudes. And |
|
| 197:33 | what we're analyzing. And we're calling uh reflectivity gradient and intercept, but |
|
| 197:39 | not, it's received aptitude Grady and the slope in the figure is about |
|
| 197:47 | -5. You look here, you see it's about the slope of -5 |
|
| 197:53 | it goes down five units for every unit. It goes silent For laboratory |
|
| 197:59 | . We expect about -1. So wrong? Well, and the reason |
|
| 198:10 | wrong is because we've neglected all those effects on amplitude coming from other effects |
|
| 198:19 | um propagation effects. And we ignored that. We applied our reasoning for |
|
| 198:27 | , not to reflectivity data but to amplitudes. So there's a magic way |
|
| 198:34 | correct for all that to what I power point process. So I'm gonna |
|
| 198:40 | this file this image right here and gonna grab it with my mouse right |
|
| 198:46 | and press everything further. So that's I've done here. So now now |
|
| 198:53 | are compressed compressed vertically. And look the little logic trend has about my |
|
| 199:00 | . So how about that? But all the uh anomalous points are still |
|
| 199:06 | and they still collect over here at top of the structure. So we |
|
| 199:12 | for all of our many mistakes and pathology trend with a correct slope just |
|
| 199:18 | compressing damage. And the anomaly is anomalous. Amazing. So uh uh |
|
| 199:27 | we we found here is a way uh look at a non lowest places |
|
| 199:33 | the earth in terms of amplitude And it successfully defines fluid anonymous by |
|
| 199:48 | . Even though we've made serious We didn't correct for propagation effects very |
|
| 199:56 | . Maybe not at all. And we neglected an eye socket. Now |
|
| 200:01 | about this. We're analyzing amplitude variation a function of offset. It means |
|
| 200:08 | variation as a function of angle, we're assuming that the velocity does not |
|
| 200:13 | everything. We know that in the of ours. He does very |
|
| 200:18 | That is uh um local anisotropy. shouldn't we really be analyzing the reflectivity |
|
| 200:29 | anti psychotropic instead of the tropics. , and they took the project away |
|
| 200:39 | me in the same week. when as they were uh probably finding |
|
| 200:49 | Avio really does conventional Ariel and we have today still today. And basically |
|
| 200:55 | same way as we did then it does reduce risk, But at the |
|
| 201:02 | in the same week when we came that conclusion for certain and and Amoco |
|
| 201:08 | 1980, or 81 maybe before you were born in, we understood |
|
| 201:17 | Uh and uh but I thought in same week, I ask myself these |
|
| 201:23 | . Can we do better if we if we don't neglect and I |
|
| 201:28 | we aspire to doing better if we to avoid these mistakes, the answer |
|
| 201:32 | yes. And we'll talk we'll talk that election. Now, let's see |
|
| 201:40 | , I'm probably good. So the as we talked about is the property |
|
| 201:49 | the interface. You know, it's those deltas ease and delta V's and |
|
| 201:53 | muse in there. It's not a of either medium. It depends on |
|
| 201:58 | different differences. So many people in profession find it easier to consider the |
|
| 202:05 | properties themselves rather than these interface So that the layer properties can be |
|
| 202:11 | from the inner properties via a process we call seismic inversion. Now, |
|
| 202:16 | a bit of a fancy term that does not the same as mathematical |
|
| 202:21 | but that's what we call it. we end up with layer properties, |
|
| 202:26 | inner property. So we don't say doing this, we don't say that |
|
| 202:31 | uh this year marvelous jumps across that . We say the share market has |
|
| 202:40 | value in the upper layer and then other value in the lower. So |
|
| 202:45 | a computation, which has its own . And that's all I'm gonna say |
|
| 202:51 | that, except that you will learn about that inversion. And of course |
|
| 202:57 | A B L. I think you that in this sequence here, You |
|
| 203:01 | have somebody talking about a B Um in an entire force you'll learn |
|
| 203:08 | things like that. But everything you here will apply to those computed layer |
|
| 203:14 | . So let's have a quick quiz and then uh have a break. |
|
| 203:23 | in a common reflection point, common midpoint gather conversion to offsets two |
|
| 203:29 | requires an accurate estimate of velocity, above and below reflecting interface. |
|
| 203:35 | is that true or false? Huh didn't hear you, What do you |
|
| 203:40 | ? True. Well now let me you, why do we need to |
|
| 203:44 | the velocities below the reflecting interface for purpose? We're converting offense to |
|
| 203:51 | So why do we need the uh velocities below to make this conversion? |
|
| 204:05 | it something to do with smells? , I know it's something to do |
|
| 204:09 | the fact that this conversion here all the angles uh involves the rays that |
|
| 204:16 | down and back up and they never below. So we don't know uh |
|
| 204:22 | this computation, converting our sense we do not need to know the |
|
| 204:27 | below the reflecting interface. In fact gonna learn opens when we do the |
|
| 204:32 | Avio analysis but for converting assist we don't need to know this. |
|
| 204:38 | the answer to this one is So this I would say this is |
|
| 204:41 | a trick question but it's a question does uh require you to read it |
|
| 204:48 | and think it through and decide whether of these points which are mentioned |
|
| 204:55 | this conversion, this accurate estimate above below. Are those all necessary to |
|
| 205:02 | this? And the answer is false you do not need to know the |
|
| 205:06 | below in order to convert process. next question, if your analysis is |
|
| 205:16 | done on migrated pre stacked gatherers to or maybe, well, no, |
|
| 205:27 | gonna go with maybe because when we the migration, we got a better |
|
| 205:31 | , but who knows what we did the amplitude. So uh, answer |
|
| 205:36 | question about what did we do to amplitudes in the migration? You gotta |
|
| 205:43 | to your local experts and he will you whether or not he has confidence |
|
| 205:47 | those migrated applications. And if he thought about it. And then you |
|
| 205:53 | , well, I'm not even gonna at this until you give me a |
|
| 205:55 | answer than that. And so then week or two or three later, |
|
| 205:59 | gonna come back and he said, , um, uh, I think |
|
| 206:04 | attitudes are pretty good in the after . So you can go ahead and |
|
| 206:09 | at pre stank migrated priest and gather you might face something bad. He |
|
| 206:15 | , oh my God, I didn't what I was doing to the |
|
| 206:18 | So the best answer for this is because it depends upon this other |
|
| 206:26 | doing his job well. And you want to just assume he did his |
|
| 206:31 | . Well, you want to talk him about it and say, |
|
| 206:34 | ralph, when you do these what did you do to the attitude |
|
| 206:39 | you're given to? Okay, number in this little rise expression, the |
|
| 206:49 | wave properties appear where intercept graded both term. All is it both of |
|
| 207:01 | ? Well, okay, so we saw it explicitly in the |
|
| 207:06 | We saw the jump in mu explicitly the grading. Now tell me where |
|
| 207:11 | saw uh in the innocent the intercept you remember is the one we actually |
|
| 207:17 | ourselves. That's the delta Z over term. And yeah, so you |
|
| 207:25 | say, well, the busy includes VP and the VP includes K plus |
|
| 207:30 | thirds mu but that's not fair because , that four thirds mu always appears |
|
| 207:37 | combination with K. So we call , give it a name and we |
|
| 207:41 | it M. And so I'm going say that there are no shear wave |
|
| 207:45 | inside the intercept, but only in gradient. And then uh in the |
|
| 207:50 | term, the same logic appears to , the answer, oops, the |
|
| 207:55 | is b okay, before The grading , the R two term, maybe |
|
| 208:03 | in terms of portions ratio. Although expression is either, you know, |
|
| 208:09 | any additional approximation. Although this expression either more complicated or contains further assumptions |
|
| 208:17 | the former looked at. So the to that is uh true. That's |
|
| 208:22 | true statement. And you can go to the previous slides too. So |
|
| 208:31 | easy to estimate. Uh I don't this word, that's easy to estimate |
|
| 208:38 | sheer property jumps at the interface by simple algebraic combination of Avio gradient |
|
| 208:44 | Is that true or false? I like nothing in this lecture was |
|
| 208:49 | So like on the. Okay. . So I gave you actually a |
|
| 208:55 | but the formula, the formula and the curvature. And so the curvature |
|
| 209:01 | never well determined. So the answer looking for here is false. Well |
|
| 209:07 | , that's what I was thinking. was like nothing looks good because it |
|
| 209:11 | easy With a simple combination. But fact the 90s because what you rely |
|
| 209:17 | is the curvature, which is Next question. The relationship between Avio |
|
| 209:25 | grade. It depends among other things whether or not the food cut that |
|
| 209:30 | across the interface. Is that Yeah, that one is true. |
|
| 209:37 | that is the basic answer. That's basic reason why a vo is so |
|
| 209:42 | in our business that this gradient the changes and the inter ship changes |
|
| 209:49 | But uh the relationship between the interception changes. If there's a fluid content |
|
| 209:56 | , then you're likely to have the to have the same sign as the |
|
| 210:01 | the intercept. That is if it's then with offset it gets more positive |
|
| 210:08 | , that's more negative, and that's we call positive, a video signal |
|
| 210:14 | a food content change and it doesn't . Uh 100% of the time that |
|
| 210:21 | happens so commonly. That is a good way to reduce the risk, |
|
| 210:29 | Oh, really? Okay, so is a good place for us to |
|
| 210:38 | . Yeah, it's 12 30 so stop right here and pick up here |
|
| 210:42 | 1 30 we'll go through to 5 . And I noticed that we didn't |
|
| 210:47 | any rain yet, but I think rain is still coming, so I'm |
|
| 210:51 | everybody's safe at home, so I'm uh stop sharing here. |
|