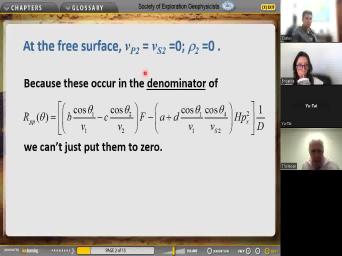
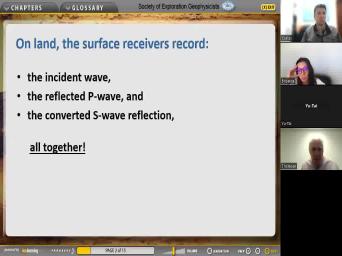
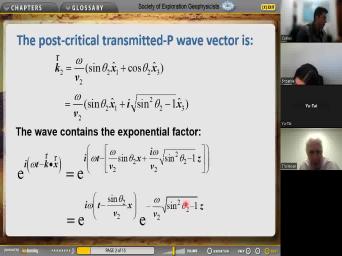
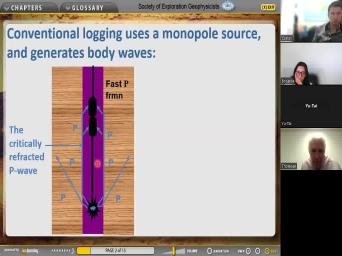
| 00:00 | Right. And Oh OK. Um this is where we finished. So |
|
| 00:22 | um this is where we finished this . And so what we need to |
|
| 00:34 | is to uh uh find these four . So we have uh two |
|
| 00:48 | this one right here and this one here and two angles. This |
|
| 00:53 | we can this one. OK. , uh of course, uh this |
|
| 00:57 | new for us, right? We , we had, we didn't have |
|
| 01:00 | angles to determine in the previous example it was normal incident. So |
|
| 01:05 | let's see what we do. Uh consider the issue of the angles. |
|
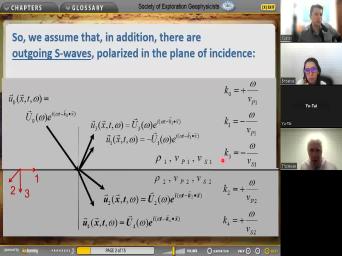
| 01:09 | here is our incoming uh ray. here is the uh those uh vectors |
|
| 01:15 | zero. I just repeated it here show uh uh that's the wave |
|
| 01:21 | Uh And uh so the wavefront is like this and here is the expression |
|
| 01:26 | the um uh for the plane And uh so this uh uh wavefront |
|
| 01:35 | , is hitting the intersection right The next wavefront, you know, |
|
| 01:40 | is a periodic wave. So next is following here. And um um |
|
| 01:46 | a short time, this wavefront is move up to here following this |
|
| 01:51 | And so the intersection point is gonna moving along this way. You see |
|
| 01:56 | intersection point moves faster, the wavefront horizontally along the interface with an apparent |
|
| 02:09 | given by this. Here's the apparent , it's the uh the actual velocity |
|
| 02:16 | by this arrow uh divided by uh sine of the angle. So here's |
|
| 02:21 | uh the sine of the angle And so uh uh sine of the |
|
| 02:26 | is uh less than one. And the apparent velocity is faster than the |
|
| 02:31 | real velocity that uh uh is one the ray parameter P sebas which we |
|
| 02:39 | before. So now, in order match the boundary conditions at all XS |
|
| 02:47 | at all times, the apparent velocity be the same for all these modes |
|
| 02:52 | the zero mode in uh incoming. uh the uh the one mode uh |
|
| 02:58 | and the two mode transmitted uh uh all have to be the same, |
|
| 03:03 | call that a concert guy who won piece of X. So this is |
|
| 03:09 | special case of Snell's law that we uh saw before. Uh So, |
|
| 03:14 | it leads to these uh uh uh equations for the sign of the reflected |
|
| 03:21 | is uh uh uh solving this equation . It's a sign of the incident |
|
| 03:26 | times VP one or VP zero. of course VP one is the same |
|
| 03:30 | VP zero, it's the same So that's that this ratio is a |
|
| 03:35 | . So it says reflected uh angle incident angle. The transmitted angle is |
|
| 03:40 | because of this ratio is not So I have a little movie here |
|
| 03:47 | uh uh built by uh my U H colleague uh Iving Lee uh a |
|
| 03:56 | years ago. And so uh uh shows what happens when um all the |
|
| 04:02 | the successive uh as you go deeper deeper, uh the uh velocities get |
|
| 04:08 | . And so that's more or less happens uh in the earth is not |
|
| 04:14 | what happens, but this hardly ever where the uh of the velocities get |
|
| 04:22 | uh smaller and smaller that hardly ever . But if it did, Snell's |
|
| 04:28 | would um lead to diving waves like . So this is a more a |
|
| 04:33 | typical um situation where we have some which are uh uh are slow and |
|
| 04:42 | which are fast. And so in case like that, it grows |
|
| 04:46 | So, so in the, the the slow layers, it bends down |
|
| 04:51 | then the fast layers, it bends , slow layers bends down. So |
|
| 04:55 | see that uh uh uh there's, can expect in most cases, there |
|
| 05:01 | be more f fast layers than slow . So uh generally, the wave |
|
| 05:07 | , will bend up. Now, law only affects the wave vectors. |
|
| 05:13 | does not affect the amplitudes. So , we've also got to have uh |
|
| 05:19 | not of two components of uh displacement two components of stresses. Remember that |
|
| 05:27 | the uh in the, the normal case, we only had to consider |
|
| 05:32 | Z displacement. And now we have consider also the X displacement. So |
|
| 05:36 | have uh four equations here coming from , but we only have 24 parameters |
|
| 05:45 | , we have uh uh the uh amplitude of the reflected wave and the |
|
| 05:51 | of the transmitted wave. And so can't solve four equations with only two |
|
| 05:59 | . So this problem uh uh uh proposed solution that we provided does not |
|
| 06:07 | . So let's have a more um proposal, let's put in there not |
|
| 06:15 | um uh reflected P and uh but reflected S and not only transmitted B |
|
| 06:23 | also transmitted S OK. So more , more plane waves you see |
|
| 06:30 | more uh uh wave numbers. So is the length of the incoming wave |
|
| 06:36 | . That's the length of this vector given by uh uh omega over VP |
|
| 06:42 | here is the length of the reflected and the minus sign uh uh indicates |
|
| 06:47 | going up. And so uh here uh another upcoming vector but it's um |
|
| 06:55 | L to vs one, the sheer in the upper media. See right |
|
| 07:00 | , we've specified, we're gonna have , one also specified above and vs |
|
| 07:05 | below and simulate two waves going So we can find solutions if and |
|
| 07:12 | if Snell's law includes all different So the ray parameter, horizontal |
|
| 07:19 | all these modes is called ray parameter . So that's the inverse of the |
|
| 07:25 | velocity and related to all these individual with the signs of the various |
|
| 07:32 | OK. So I've got some movies and uh let's see here. I |
|
| 07:39 | , I don't remember whether I uploaded movies. I, I think I |
|
| 07:43 | not. OK, be on I will uh I will upload the |
|
| 07:49 | um uh tonight and then you can at them um during the week and |
|
| 07:56 | can talk about them next week. have a movie for Rage and a |
|
| 08:01 | for Wave Front. So um um sorry about that. I forgot to |
|
| 08:08 | that. OK. So I, , I'll do that tonight. |
|
| 08:17 | So now what we have then is uh these four equations now with more |
|
| 08:24 | . Matter fact, I didn't uh count them up. But uh |
|
| 08:28 | we, we do have enough enough now to uh uh to uh oh |
|
| 08:35 | . So here we have four equations four are not before we had two |
|
| 08:40 | . Now, we have um four and the two extra unknowns are the |
|
| 08:46 | of the two sheer way before we only a uh uh amplitudes for the |
|
| 08:54 | yeah, uh for the reflected and p wave. Now we have two |
|
| 09:00 | unknowns for the sheer wave. And so we have four operations and four |
|
| 09:05 | . And there's lots of opportunities like said before to make the mistake in |
|
| 09:10 | conventions. And for years and uh the literature was wrong on its |
|
| 09:16 | a century ago. But the correct uh uh uh uh are now called |
|
| 09:22 | not Zurer Equations. And they can found in many modern textbooks. My |
|
| 09:29 | is the one by A and Uh uh I suppose that um uh |
|
| 09:37 | students here don't know Arne Richards but I think uh uh uh you |
|
| 09:42 | , do you have this book? . And Richards. Yeah. Uh |
|
| 09:47 | , uh uh it's a good book uh they clearly discuss the reasons for |
|
| 09:55 | of these various conventions on sign where minus signs go, they discuss that |
|
| 10:02 | in, in detail and by fully the conventions, they avoid the |
|
| 10:08 | This is a picture of Mr He died about in 1930 I |
|
| 10:17 | Um um but he uh uh was brilliant German um mathematician physicist. And |
|
| 10:26 | he hi his name is given right . So these are the exact equations |
|
| 10:33 | the incident of an uh plain incident . And also by the way, |
|
| 10:37 | , he showed the uh equations for incident uh SV waves and for in |
|
| 10:44 | uh uh sh waves, he did all and uh done it correctly. |
|
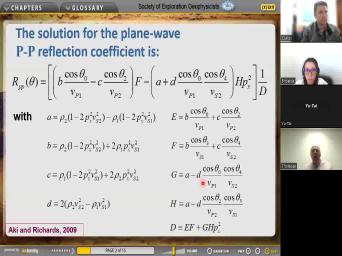
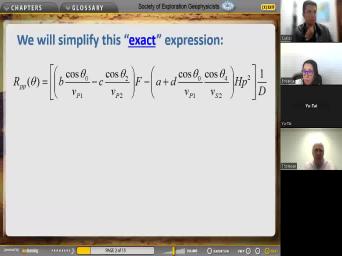
| 10:51 | so let me show you what the looks like, well, it looks |
|
| 10:57 | a mess. This is only the results for the P for the PP |
|
| 11:03 | , incoming P and outgoing P And so we have a complicated formula |
|
| 11:10 | . And uh everywhere in the formula see terms which are defined down |
|
| 11:15 | So here's B defined and C is down here and F is defined over |
|
| 11:21 | . And so you see lots and of notation and hidden inside here. |
|
| 11:27 | Here's one more and uh uppercase G down here. What a mess. |
|
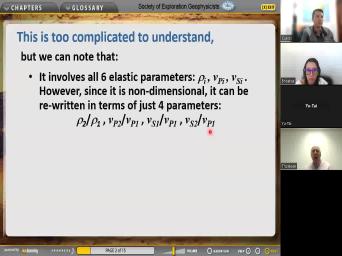
| 11:33 | so um uh furthermore, uh I think when you look at |
|
| 11:39 | you, you think that for goodness , I can't understand that and don't |
|
| 11:45 | um um this skirt, nobody understands including and Richards. I think uh |
|
| 11:54 | think ay is now dead and Richards a few years older than me. |
|
| 12:01 | . Uh but it really is too . But if you look at that |
|
| 12:06 | , it involves all six elastic parameters is density velocity and sheer velocity on |
|
| 12:14 | sides of the interface, but it's dimensional, it's a reflection coefficient, |
|
| 12:20 | has no dimensions. So it must then that uh means six parameters appear |
|
| 12:30 | non dimensional form. And so uh uh so uh uh uh uh in |
|
| 12:38 | only on the ratio of these two and these three ratios of excuse me |
|
| 12:46 | um depends on these uh this ratio densities and these three ratios of |
|
| 12:56 | Now, you could choose to normalize velocities in other ways you see |
|
| 13:01 | I've normalized uh all three velocities with one. So you could do it |
|
| 13:08 | way. But uh uh you got end up with three non dimensional measures |
|
| 13:13 | velocity and one non dimensional measure of . And uh that's makes four independent |
|
| 13:24 | . And furthermore, you noticed in previous uh expression there is no |
|
| 13:30 | And so of course, there's no because when you look at the cartoon |
|
| 13:37 | the problem, there is no characteristic and there's no characteristic time. So |
|
| 13:45 | means there's no characteristic wavelength and no frequency. So it's got all the |
|
| 13:54 | of frequency that's really important because what means is, you know, what |
|
| 14:02 | doing is we're analyzing only uh one at an incoming plan way. But |
|
| 14:09 | course, our data doesn't look like our data has wavel lists which are |
|
| 14:15 | localized in time. And the, time localized wavelengths are sums of these |
|
| 14:24 | waves which go on forever. Uh near the arrival time of the |
|
| 14:29 | they reinforce uh uh constructively at uh , at, at longer times and |
|
| 14:37 | distances, they interfere destructively. So , you know, wavel, which |
|
| 14:46 | know, is a compact wavelength is up of these infinite plane ways. |
|
| 14:54 | since they all reflect uh uh with same uh parameters independent of frequency, |
|
| 15:00 | don't have to analyze an incoming we analyze an incoming plane wave and |
|
| 15:06 | we add them all up subsequently. when we add, yeah. |
|
| 15:11 | so when we add, uh if add them up uh to make an |
|
| 15:15 | wave, we get an incoming add them up to get the external |
|
| 15:22 | uh uh the, the reflected it's the same wavelength because they add |
|
| 15:27 | in the same way, that's really , that we have to only analyze |
|
| 15:33 | plane wave component. Even though we that that's not a realistic uh um |
|
| 15:39 | description of what's going on. We that we can always do the fourier |
|
| 15:45 | composition afterwards. So we only have consider the uh the single plane wave |
|
| 15:56 | . So if you look closely at uh uh previous uh uh formula, |
|
| 16:01 | reduces to the previous result at theta zero. Let's, let's just go |
|
| 16:06 | here. It's so oops, so thing. But at normal incidence, |
|
| 16:15 | got um coate equals one. So term is here co two. this |
|
| 16:22 | gonna be for uh uh transmitted wave that's also gonna be a one |
|
| 16:28 | but we have some things which go here. See here. Hm. |
|
| 16:35 | Yeah, yeah, look at this in normal incidence PX equals zero. |
|
| 16:42 | uh uh uh uh A is gonna zero. And uh let's see. |
|
| 16:49 | Well, you, you can go here uh recognizing that at normal incidence |
|
| 16:54 | equals zero. A lot of these go away and you can do the |
|
| 16:59 | for the algebra for yourself uh after and you'll find that at normal incident |
|
| 17:05 | data equals zero, this thing reduces the result that we had before. |
|
| 17:12 | , that's good news. So we this right? And we did the |
|
| 17:15 | one right now. This is an thing. If all the angles are |
|
| 17:25 | , this reflection coefficient is real. , the reflected wavelength will have the |
|
| 17:31 | phase and the same shape as the wavelength. So let's go back here |
|
| 17:39 | . OK. So look at, you see anything that's imaginary in here |
|
| 17:44 | all these angles? Of course, angles are gonna be real. Uh |
|
| 17:49 | everything here looks like it's real. I um before we think that this |
|
| 17:57 | a closed subject, let me point to you that we will discover later |
|
| 18:05 | this afternoon cases where some of these , some of these uh trigonometric functions |
|
| 18:15 | not real. I mean, they real, don't they, what, |
|
| 18:18 | could be more real than the cosine an angle? We learned this in |
|
| 18:24 | trigonometry and uh uh uh in high . But I, I can, |
|
| 18:31 | can tell you that hidden within stuff already developed, we've already developed uh |
|
| 18:38 | ideas which are gonna lead to surprising including making some of these trigonometric functions |
|
| 18:52 | under certain circumstances. So when I this right here says, if all |
|
| 19:01 | are real, I know you're thinking , of course, the angles are |
|
| 19:04 | but turns out they're not, of , in some cases, we're gonna |
|
| 19:10 | the angles are complex. Isn't that ? OK. So keep that in |
|
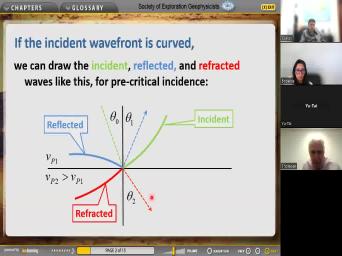
| 19:21 | . So here is Nels Law for two waves, incident and transmitted P |
|
| 19:26 | angle. So this is uh um the, the apparent velocity for the |
|
| 19:32 | uh for the incident wave and the velocity for the transmitter wave. This |
|
| 19:38 | a statement of uh uh I mean of Snell's law. And so uh |
|
| 19:47 | look like any particular uh surprises We solve this for the transmitted |
|
| 19:52 | Sine 32 looks like this. suppose we have a case where VP |
|
| 20:01 | is bigger than BP one. So fraction is more than one. Now |
|
| 20:08 | that suppose this fraction is two and sign data is 0.7 sine theta zero |
|
| 20:23 | 0.7. You, you can imagine we have an infinite angle coming in |
|
| 20:28 | uh uh a large angles. So sign of that infinite angle is 0.7 |
|
| 20:34 | that times two. It's easy to where you have a lower medium which |
|
| 20:40 | twice as fast as the other So two times 0.7 is 1.4. |
|
| 20:47 | we just kind, we just imagine case where the sign of the angle |
|
| 20:54 | the lower medium that is bigger than . How can we have a sign |
|
| 20:58 | bigger than one. That's what it here. If we just imagine the |
|
| 21:03 | , a plausible case where the s the transmitted angle is bigger than |
|
| 21:08 | I get this, the cosine is the square root of one minus sine |
|
| 21:13 | . So if this is bigger than cosine, theta is imaginary. |
|
| 21:20 | Suddenly that expression which we looked at not inserts two slides ago, it |
|
| 21:27 | complicated. but now we see it's complicated because some of those Trigon meric |
|
| 21:33 | might be imaginary, might be Just think what that can mean. |
|
| 21:42 | , uh put that on hold for moment, don't think what that |
|
| 21:46 | We are gonna consider what that means shortly. Now where, where, |
|
| 21:56 | does this happen? It happens when uh uh theta uh zero is big |
|
| 22:02 | . So the angle where it, the uh transmitted angle transitions from real |
|
| 22:07 | complex happens where the this angle theta is one that happens at a certain |
|
| 22:15 | angle for the infinite angle um uh for Anderson's law. And so uh |
|
| 22:23 | uh when, when the incident angle is bigger then thrown here, that's |
|
| 22:31 | we're gonna get this uh a strange where the sign of the transmitted angle |
|
| 22:38 | bigger than one uh for bigger And you can imagine we have uh |
|
| 22:50 | angles like that in our data all time. Now, uh uh le |
|
| 22:54 | le, let's just think here uh we normally design our survey such |
|
| 23:01 | uh uh the angles at the uh uh target horizon are something like somewhere |
|
| 23:09 | 30 degrees and 45 degrees. Uh , uh we, we fix the |
|
| 23:15 | length of our bread such that the the angle of incidents at the target |
|
| 23:26 | is somewhere between 3045 degrees, maybe bit bigger, maybe a bit |
|
| 23:31 | but, you know, in that . But think what that means that |
|
| 23:35 | uh for the same maximum offset from targets, for shallower reflectors, the |
|
| 23:44 | angle could be a lot bigger than degrees. And there you're likely to |
|
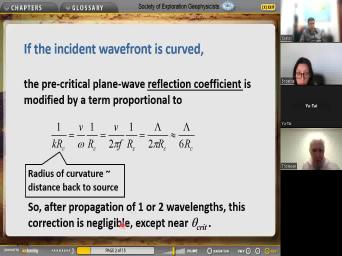
| 23:51 | the kinds of uh phenomena that are from this post critical reflections. |
|
| 24:03 | we don't even have to go out far before we get into trouble because |
|
| 24:08 | the angle of incidence, it gets be close to the critical angle, |
|
| 24:12 | even at the critical angle yet, it gets close to the critical |
|
| 24:16 | then the curvature of the incident wavefront a correction and we can't use the |
|
| 24:22 | wave coefficients that we do that up . Now, we've looked at plain |
|
| 24:29 | reflection car efficient at ignoring the curvature any real wavefront. And that's normally |
|
| 24:37 | , except that for angles of incidents close to the critical angle which we |
|
| 24:45 | defined. OK. Now, keep in mind. Uh funny stuff is |
|
| 24:56 | be happening. Uh when the angles large enough, if the lower |
|
| 25:03 | if the reflecting medium is faster than uh upper medium. Now, I |
|
| 25:10 | showed you the picture the formula for the uh reflected amplitude reflection coefficient reflection |
|
| 25:20 | curious what the OK here is what transmission coefficient looks like. It looks |
|
| 25:28 | uh uh simple. But that's you know, we have a lot |
|
| 25:31 | embedded um notation here. Uh uh quantity F and this quantity D were |
|
| 25:39 | on the previous figure. So it's not as simple as it |
|
| 25:47 | So the main thing I wanna show , this is this quantity is not |
|
| 25:52 | equal to one minus the reflection coefficient at normal incidence. So if you |
|
| 26:00 | embedded in your mind, that transmission is one minus reflection coefficient, that's |
|
| 26:05 | , but only for normal incidents, for most of our data. |
|
| 26:13 | these transmitted waves are also called refracted . Uh So when we said in |
|
| 26:19 | um title of this lecture, we of reflections and refraction, we could |
|
| 26:25 | said reflections and transmission. And of , both both things are gonna happen |
|
| 26:30 | every single interface in the subsurface. . So um uh Mr Zober uh |
|
| 26:40 | finished yet. This is what he up with for the conversion car |
|
| 26:45 | This is for the uh the, , the coefficient for converting from P |
|
| 26:51 | S um at a given angle theta uh this, this is actually |
|
| 27:03 | the infinite angle theta zero. So see that and it's got uh uh |
|
| 27:09 | , it's not as complicated as the coefficient, but uh more complicated than |
|
| 27:16 | transmission coefficient. This is the conversion from P to S and an important |
|
| 27:22 | about this is this initial sign data . So what that says is that |
|
| 27:34 | uh uh at normal instance where a equals zero, this is gonna be |
|
| 27:39 | zero. So that means everything is be zero. And so we're gonna |
|
| 27:43 | the conversion coefficient at normal lens should zero. That's what this equation in |
|
| 27:52 | uh formula says. And furthermore, anti symmetric that is to say if |
|
| 27:58 | have a positive offsets, you'll have theta zeros, negative offsets and negative |
|
| 28:04 | theta zeros. And so the sign a of a negative angle is also |
|
| 28:10 | . So th this uh amplitude is be antis. Now uh we do |
|
| 28:24 | this stuff. Uh uh uh uh do see data which is governed by |
|
| 28:30 | equations like this. We don't normally uh the uh coefficient we, we |
|
| 28:38 | normally see in our data. Uh would depend upon the transmission coefficient for |
|
| 28:44 | to S uh in the, for , in the ocean bottom context that |
|
| 28:50 | showed yesterday. Uh uh I said the, the most energetic arrival is |
|
| 28:56 | one that uh converts upon reflection, the one which convert converts upon transmission |
|
| 29:03 | the ocean. Into the, into sea form that's governed by this |
|
| 29:08 | And so uh we understand from uh Mr Zrt that normally this is a |
|
| 29:16 | number when we apply it to uh cases like um the C four. |
|
| 29:24 | um you know, I am not of a single data set that I'm |
|
| 29:29 | with where we've ever had to think about the uh the issue of conversion |
|
| 29:37 | transmission, only conversion upon uh uh . This one here. OK. |
|
| 29:47 | , uh with that discussion, a of the, the exact reflection coefficients |
|
| 29:56 | transmission coefficient and, and uh and for the uh this model of uh |
|
| 30:04 | isotropic uh above and below half space and below all that's uh uh |
|
| 30:11 | But it's a problem which we know to solve as solve over a century |
|
| 30:16 | . And so, uh um uh see what we have learned about |
|
| 30:21 | I forgot who's next. So I'm start off with uh uh New la |
|
| 30:26 | Is this one true or false? angles of the outgoing way are determined |
|
| 30:31 | a Snell's Law, true or Say that again, I, I |
|
| 30:46 | hear you. You mean to speak loudly? This is not Snell's |
|
| 30:51 | you're right. Very good. you, I, you were not |
|
| 30:55 | by and this is a trick question you did not get fooled. Very |
|
| 30:59 | . This is not a good statement , of Snell's law. OK. |
|
| 31:04 | uh for uh the other students that you were thinking uh if you missed |
|
| 31:08 | , uh go back and check uh previous uh he was notes. |
|
| 31:14 | So this one comes to Carlos the exact plane way reflection coefficient can |
|
| 31:22 | written in terms of these four non parameters. Is that true or |
|
| 31:36 | Carlos, let me hear your I think it's true. Uh |
|
| 31:45 | th this is true. Now, is not a set of four that |
|
| 31:48 | showed you earlier. This is a set, but this set is just |
|
| 31:52 | good. So here we've uh uh we've uh normalized the, the, |
|
| 31:58 | share, the share wave velocities with uh uh uh infinite share wave |
|
| 32:02 | So that's just as good. Uh So uh the, the way you |
|
| 32:08 | uh uh isn't important so long as have three independent uh quantities here. |
|
| 32:16 | . So that uh that's good. A Brier um true or false since |
|
| 32:24 | of the terms and the expression for exact plane reflection Carri are real. |
|
| 32:29 | cof fish itself is real true or . If I understood correctly explanation, |
|
| 32:36 | think it's false. Yes, that's because this is not true here. |
|
| 32:41 | is not true that all the terms real. In all cases. In |
|
| 32:45 | cases, there are imaginary, other are complex. So this uh uh |
|
| 32:51 | you are, you are correct. . Very good. Now, it |
|
| 32:57 | back to you uh li Lei. So uh let's consider a case here |
|
| 33:03 | the uh uh sediment and the salt . So, you know that uh |
|
| 33:07 | se uh salt is very fat. we have uh uh uh it's considered |
|
| 33:13 | sediment and the incoming uh and the medium is 2000 m per second. |
|
| 33:19 | inside the salt, it's 4000 m second. So uh um what is |
|
| 33:26 | critical angle Say? Say that I just didn't hear you c it |
|
| 33:34 | uh answer C OK. So tell your um uh your, your thinking |
|
| 33:40 | , that's correct, by the So tell me your thinking and speak |
|
| 33:52 | . So the, the ratio of velocities is one half. So that's |
|
| 33:55 | same half here. But uh uh critical angle is the, the angle |
|
| 34:01 | who, who's uh uh uh uh the angle whose s is equal to |
|
| 34:06 | half and that turns out to be degrees. And so if you don't |
|
| 34:10 | that, that's a good thing to . It's, the s of 30 |
|
| 34:13 | is one half. Another thing is of 45 degrees. With what? |
|
| 34:19 | , you mean? Uh uh II said it wrong. Um uh A |
|
| 34:24 | of uh 90 degrees is one. uh so uh those are uh it's |
|
| 34:31 | if you can remember that the sign 30 degrees is one half. |
|
| 34:35 | So, so much for a line exact uh expressions. The main thing |
|
| 34:43 | we learned out of that exact expression that it's too complicated for us to |
|
| 34:50 | much about reflection, except what we talked about. Instead, we've got |
|
| 34:56 | simplify someone. Uh It's very common geophysics that we make simplifications. We |
|
| 35:05 | approximations. You know, we've already about this a lot. We, |
|
| 35:09 | approximate that the media are isotropic and know that's not true, but we |
|
| 35:15 | it anyway. And, but it's for us to remember that that's just |
|
| 35:19 | approximation. Now, we make lots other approximations here. We're going to |
|
| 35:26 | the previous expression by assuming that the uh uh the contrast across the horizon |
|
| 35:33 | small. Uh So that means the medium is pretty similar to the lower |
|
| 35:41 | . OK. So, uh the results were exact but almost useless for |
|
| 35:48 | because real a don't obey uh uh equation because they're not isotropic, |
|
| 35:59 | They're not exactly elastic. Either somebody asked that in the day uh day |
|
| 36:04 | yesterday or maybe our, our rocks elastic. And the answer is uh |
|
| 36:09 | no, you're not perfectly elastic. we will come to that in lecture |
|
| 36:20 | . Furthermore, real end phases are always uh perf perfectly plain uh |
|
| 36:27 | you know, that um um uh interface with say uh uh a shale |
|
| 36:37 | and a sandone below something like that is probably not mathematically smooth, |
|
| 36:45 | a mirror. It's probably the result a sedimentary process, you know, |
|
| 36:51 | go back in geologic history and imagine that interface got constructed. It got |
|
| 36:58 | over many years as a result of sedimentary process. So it might, |
|
| 37:04 | not be exactly playing like a It might have uh wiggles in |
|
| 37:10 | It might have, you know, , a uh uh uh small hills |
|
| 37:17 | valleys and then uh uh it might been bent by tectonics. And then |
|
| 37:25 | also know that the in incident wave always curved because the infinite wave is |
|
| 37:31 | a plane wave, it comes from localized source and it spreads outward from |
|
| 37:37 | localized source with curvature everywhere. we never have in uh in our |
|
| 37:53 | instances where we have an interface. uh and uh on either side of |
|
| 37:59 | , we have homogeneous rock, it happens and we have nearby other layers |
|
| 38:10 | happens. And then, furthermore, too complicated. So uh what we |
|
| 38:17 | to do is find ways to make anyway. OK. So we're gonna |
|
| 38:28 | an appropriate approximation. And mo and often, not always, but most |
|
| 38:33 | the appropriate approximation is that the two bodies above and below that interface are |
|
| 38:41 | . So the contrast is small. , we're gonna uh the incident angle |
|
| 38:47 | not too large. Uh uh we're going to be able to easily |
|
| 38:53 | angles up to like uh before we uh we're gonna be OK. |
|
| 38:59 | long as we don't get too close the critical angle. And for |
|
| 39:05 | we're going to assume that the media isotropic, they are perfectly elastic and |
|
| 39:10 | are no other uh other interfaces No, before we begin this discussion |
|
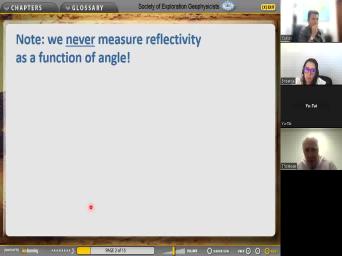
| 39:23 | a vo we got to remember that never measure reflectivity as a function of |
|
| 39:29 | , never ever. Instead what we is received amplitudes as a function of |
|
| 39:37 | . OK. So uh we're gonna convert all sets to angles, but |
|
| 39:41 | gonna be a complicated calculation. The uh is what we receive. But |
|
| 39:50 | is the incident amplitude? Maybe we what is the incident amplitude when it |
|
| 39:55 | our source by the time it gets to the target reflector, it has |
|
| 40:00 | sorts of things happening to it. do not know the incident amplitude. |
|
| 40:07 | so the reflection coefficient, the reflectivity the ratio of this received amplitude to |
|
| 40:14 | local incident amplitude song given this uh this is what we measure, this |
|
| 40:26 | what we want. So uh first to do is to convert offsets to |
|
| 40:32 | . So that means you have to an accurate velocity field in the entire |
|
| 40:36 | all the way down from the all the way down to the |
|
| 40:41 | And furthermore, it's gonna probably be anisotropic velocity distribution. But uh |
|
| 40:48 | and so you never know that And under some circumstances, uh uh |
|
| 40:55 | circumstances, you can have a good , but you never know it |
|
| 40:59 | So you never know the, the uh you never know the incident angle |
|
| 41:11 | . But if we make an estimate the velocity field and the overbook, |
|
| 41:17 | we can trace rays through the V model from the source to the uh |
|
| 41:23 | reflector and back to the uh Uh And so, in that |
|
| 41:30 | we're gonna determine the incident angle at reflector as an estimate. Now, |
|
| 41:43 | this convolutional description of wave propagation, had a source with a source wavelet |
|
| 41:51 | down reflecting and propagating back up. this reflection happens at lots of different |
|
| 41:58 | , all of those come back to instruments. And here's our instrument, |
|
| 42:01 | receiver response and then here's our computing after uh uh we compute using the |
|
| 42:09 | that comes up the wire from the . And then in addition to all |
|
| 42:13 | stuff, we have noise. So of these things affect the amplitude in |
|
| 42:20 | angle dependent way. So let's think this, for example, uh uh |
|
| 42:26 | uh the propagation uh uh going down uh a as it goes down, |
|
| 42:33 | passes. Uh So it's head, headed down to the uh top of |
|
| 42:38 | reservoir and on its way it passes other interfaces and every one of them |
|
| 42:44 | a transmission coefficient which is varies with got it. And furthermore of the |
|
| 42:52 | offsets have longer path lengths in the . So they have more attenuation in |
|
| 42:58 | subsurface. So those are two trivial of how there's an angle dependence em |
|
| 43:05 | in here. And it's a complicated . Uh uh uh We never have |
|
| 43:12 | ability to figure that out in We never have enough information to figure |
|
| 43:19 | all the uh things which are happening the amplitude on the way down also |
|
| 43:25 | the way up. Um I and um what we really want, we're |
|
| 43:33 | not interested in all these things. we're interested interested in is the variation |
|
| 43:38 | reflectivity as a function of angle, we get and our data is contaminated |
|
| 43:45 | all this other stuff. Let me up here. Once it gets to |
|
| 43:55 | computer, we uh do all kinds things in the computer which may affect |
|
| 44:04 | uh amplitude in an angle dependent So uh what we like to do |
|
| 44:14 | what we call true amplitude imaging. so I think we're getting better at |
|
| 44:21 | uh as we get to be But uh uh I, I uh |
|
| 44:28 | I am not um an expert in matters. So I, I'll uh |
|
| 44:34 | suggest that you should ask Professor Joe he's talking about imaging, ask him |
|
| 44:40 | it does to amplitude both in the and in the uh uh in the |
|
| 44:47 | image, gather that go into the , what has the algorithm done to |
|
| 44:53 | amplitude? And I think what he's do it gonna tell you is, |
|
| 44:58 | , that depends on which algorithm you . It depends on which program you |
|
| 45:02 | use. And so what it means the implication here is is that if |
|
| 45:08 | have a data set which comes from , from a AAA an area with |
|
| 45:17 | social service geometry and you have to a lot of heavy migration to get |
|
| 45:22 | image. Maybe that means that the a vo is affected by the migration |
|
| 45:32 | . And you have to know about before you take that apparent a vo |
|
| 45:40 | . So check with your uh resident before you do an a vo analysis |
|
| 45:47 | any migrated data. OK. most of us don't uh use uh |
|
| 45:59 | for doing this kind of analysis which wrote ourselves. And furthermore, we |
|
| 46:04 | use software which was written by anybody we know. Normally we use software |
|
| 46:09 | we uh bought or, or licensed some third company, you know, |
|
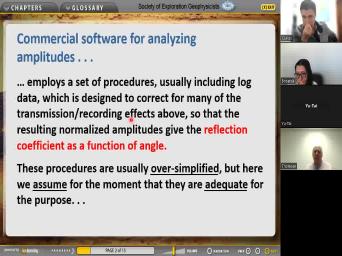
| 46:15 | Hampton Russell and what they've done is employed a set of procedures and those |
|
| 46:22 | usually include looking at log data. proce set of procedure is designed to |
|
| 46:28 | for many of the other effects which mentioned above. And they do that |
|
| 46:34 | order that the resulting normalized amplitudes resistance as a function of angle. |
|
| 46:43 | Um So after you apply one of software packages, we're gonna give you |
|
| 46:51 | which looks like a reflection coefficient as function of angle, but without uh |
|
| 47:02 | getting myself into trouble so that lawyers calling me up, I'm gonna say |
|
| 47:08 | these procedures are often oversimplified, often with whatever software package you use. |
|
| 47:18 | , I'm gonna ignore that issue for and I'm going to uh proceed with |
|
| 47:24 | analysis and leave the assumption that after pass your data through Hampson Russell software |
|
| 47:31 | uh uh fo or anybody else that uh these are gonna be adequate for |
|
| 47:36 | purpose. Now, oh, I wanna think about reflection coefficients. |
|
| 47:46 | II, I got, I have question here and it's about the units |
|
| 47:51 | the amplitudes because yeah, I have that you can find in seismic, |
|
| 47:56 | lot of different like ranges for the amplitudes that you have in your |
|
| 48:03 | And basically there is like a standard like for this, for this software |
|
| 48:08 | like normalize and actually get the final that actually is given to the |
|
| 48:16 | OK. So, so uh let's about this a little bit. Uh |
|
| 48:19 | First, let's imagine you're sitting looking some seismic data on your workstation and |
|
| 48:25 | got uh s uh suppose you um suppose you sort the data into a |
|
| 48:33 | midpoint gather. And so you're looking that gather and, and it's got |
|
| 48:38 | move out and all the nearby reflections everything. It's got all the real |
|
| 48:42 | issues in there. And you can that at the furthest offsets the amplitudes |
|
| 48:51 | your favorite arrival are different than for offsets. So there's an apparent a |
|
| 48:58 | of effect in your data. And you know that that is due to |
|
| 49:05 | uh a combination of reflectivity variation with and with transmission um uh variations with |
|
| 49:18 | , all the things that we talked up here, what you're looking at |
|
| 49:23 | received, receives aptitudes and it's got these effects in here which uh are |
|
| 49:32 | very difficult to get rid of. so we have software that attempts to |
|
| 49:37 | that. And right now I'm saying let's say it's adequate for the |
|
| 49:42 | however. OK. So, so do that. So, so now |
|
| 49:46 | run your data. Oh, before do that, look at your data |
|
| 49:51 | move your mouth over the data and you park your mouse over some point |
|
| 49:57 | that wiggle, then you can see uh a readout of what is the |
|
| 50:02 | amplitude for that wiggle at that time position and it'll be a number normally |
|
| 50:09 | 1000 and minus 1000. Mhm. , you know, immediately that somebody |
|
| 50:18 | done something in the computer to normalize uh uh the the seismic data uh |
|
| 50:28 | that scale binance the house into Now, you know that reflectivity |
|
| 50:40 | is gonna be a small number reflectivity gonna be a number a lot less |
|
| 50:47 | one. So there's maybe four orders magnitude difference. And um and uh |
|
| 50:54 | the size of the numbers you're looking . So this business of normalization, |
|
| 50:59 | are we normalizing things? So that uh um uh that is a uh |
|
| 51:11 | problem which uh uh these software packages uh a attempt to solve. And |
|
| 51:19 | , uh uh right now, uh , let's assume that that uh uh |
|
| 51:27 | , we pass our seismic data through of these commercial packages and come up |
|
| 51:32 | some reflectivity on the other side. suppose the reflectivity is not given as |
|
| 51:39 | uh a wiggle, but let's suppose given as a curve. So it |
|
| 51:43 | that the uh the amplitude as a of offset of the, the peak |
|
| 51:49 | the wavelength, we replaced the wave a single number amplitude at the peak |
|
| 51:55 | the wavelength. And suppose it's been uh uh uh uh normalized. So |
|
| 52:01 | a number of the order of You know, it's, it's, |
|
| 52:05 | between uh uh uh 10% and minus and it's just AAA curve on a |
|
| 52:13 | as a function of angle. So what, yeah, you might expect |
|
| 52:20 | get from Hampton Russell and from Frugal when they've done all their stuff |
|
| 52:26 | And so uh we're gonna leave for . The question of uh did they |
|
| 52:31 | it? Right. Um I think how we're gonna think about this curve |
|
| 52:37 | amplitude versus uh uh offset a amplitude angle is what we want. And |
|
| 52:49 | let's assume for now that they did right? And that you can take |
|
| 52:54 | that curve. So what are we think about that curve now? |
|
| 53:00 | So this was the exact question that had. Yeah. Uh we're gonna |
|
| 53:09 | this exact expression in a couple of . Number one, we're gonna reformulate |
|
| 53:15 | exactly in, in these terms. uh So it depends upon only the |
|
| 53:20 | in uh density here is the jump density divided by twice the mean density |
|
| 53:28 | the jump in key velocity, the in sheer velocity and this velocity |
|
| 53:33 | So here are four different terms. And we know that this thing uh |
|
| 53:40 | it apparently shows six parameters, six parameters in there. But we talked |
|
| 53:46 | about how it's got to be non . So there's only four independent variables |
|
| 53:51 | . We're gonna pick these four jump and density, non dimensional jump in |
|
| 53:57 | , non dimensional jump in vp non jump in vs and the velocity ratio |
|
| 54:04 | uh velocity uh This V bar is average velocity above and below. And |
|
| 54:12 | is the average sheer velocity above and . And here we're taking this |
|
| 54:17 | OK. So uh that's easy to . That's not, not easy, |
|
| 54:23 | you know, and you can see how you could do that. And |
|
| 54:27 | we're gonna assume weak elastic contrast. is, we're gonna assume that this |
|
| 54:34 | in density is small compared to one velocity is small com this jump in |
|
| 54:39 | small compared to one, this jump sheer velocity is small compared to |
|
| 54:45 | And we're gonna not make any assumptions this yet. And then we're gonna |
|
| 54:51 | a first to order tailor approximation after done all this reformulation. And uh |
|
| 54:58 | uh then we're gonna assume that uh uh these three are small numbers, |
|
| 55:04 | one, this one and this one small number a first order tailor |
|
| 55:08 | And then this is what we come with, we get the linearized plane |
|
| 55:15 | wave reflection coffi. So this uh the uh special case of um the |
|
| 55:22 | equations conforming to all those assumptions that just made. And you see, |
|
| 55:27 | looks pretty simple. So look, look inside here, let's look inside |
|
| 55:34 | . These three parameters contain all of um uh physical um uh parameters of |
|
| 55:46 | subsurface. It, it, it tells you the jump. Well, |
|
| 55:50 | le let's look at this one. , this is uh R zero is |
|
| 55:56 | jump and uh uh be wave And so you can see that when |
|
| 56:03 | , at normal incidence with eight equals , this term goes away and this |
|
| 56:07 | they go. So this is the incidence reflection coefficient. And uh guess |
|
| 56:13 | ? It's, it's what we found from uh the not zip equation. |
|
| 56:20 | . That's good. That's encouraging. , the rest of it at, |
|
| 56:24 | nonzero theta it's gonna be different than exact expression. But the good news |
|
| 56:31 | it's fairly simple and we can uh it. It's got what we call |
|
| 56:35 | gradient term R two here. And one depends upon the jump in |
|
| 56:40 | fractional jump in VP. And the jump in sheer modules, this is |
|
| 56:46 | sheer velocity, this sheer modulus multiplied this factor here, which is more |
|
| 56:53 | less close to one. And then , this coefficient here is called the |
|
| 56:59 | turn. And that's not a simple jump in VP. Now to get |
|
| 57:09 | , we also did the following. also assumed we also used these relations |
|
| 57:17 | which says th this is simply chain calculus. This says that the fractional |
|
| 57:22 | in P wave impedes is equal to fractional jump in uh the P plus |
|
| 57:29 | fractional jump intensity. And furthermore, fractional jump and sheer modules which we |
|
| 57:35 | here is given by twice the fractional and vs plus the fractional jump in |
|
| 57:44 | . So that's just plain plain uh uh chain calculus. So this is |
|
| 57:53 | what is sometimes called the Bork Fel uh named after uh a German geophysicist |
|
| 58:00 | this century uh who did a similar but not quite the same. So |
|
| 58:06 | best way to describe this is to it the linearized plane, the weight |
|
| 58:13 | car and linearized means it's as only which are linear in these small quantities |
|
| 58:19 | here. And here. Now, other ways to uh uh implement the |
|
| 58:25 | idea of a weak elastic contrast with different parameterization. And let me just |
|
| 58:32 | you one here, here is one parson's ratio. So uh I'm only |
|
| 58:40 | you the uh uh the gradient term and it looks like it's simpler. |
|
| 58:45 | let's go back here. This is , maybe uh maybe not simpler, |
|
| 58:53 | it's, it's, it's definitely This is the gradient term which uh |
|
| 58:57 | is this is the simplest way of it as a matter of fact, |
|
| 59:01 | we could write it here in terms the change in power ratio. So |
|
| 59:06 | look what we have here. Um changing Parsons ratio multiplied by nine |
|
| 59:13 | OK? And here we have this um uh a ratio here involving the |
|
| 59:18 | value of parson ratio above and And then here's the jump in cross |
|
| 59:24 | R again and the jump in VP the jump in D. So this |
|
| 59:28 | is definitely more complicated. However, at this Mark Smith, if you |
|
| 59:37 | to have the case that the average of ARS ratio is one third, |
|
| 59:42 | this term all goes away because of . OK. So if, if |
|
| 59:47 | bar is one third, then this is zero and suddenly everything is |
|
| 59:56 | Well, that's true. Uh And would uh as a matter of |
|
| 60:00 | this is, this is exactly equivalent the expression on the previous page. |
|
| 60:05 | uh if you ignore this second it's not exactly true. And |
|
| 60:11 | in, in fact, uh it's not really a good approximation. |
|
| 60:17 | example, uh here is a common that the velocity ratio is about |
|
| 60:22 | So in that case, the uh uh the average value of uh poisons |
|
| 60:28 | is not one third, but it's . And in that case, this |
|
| 60:35 | turned into this, which is not uh uh I would say it's not |
|
| 60:41 | that simple. So um other people to uh write this gradient opera gradient |
|
| 60:52 | in terms of the leme, leme . So again, you can say |
|
| 60:58 | this is more complicated than the first and it's less useful. And the |
|
| 61:02 | of course is because this gourmet parameter appears in any uh wave theory uh |
|
| 61:11 | any wave propagation expression unless it's forced like you like it's forced in here |
|
| 61:18 | making a complicated um result. So return to the uh uh previous |
|
| 61:27 | And then say we, we are we can regard the intercept, the |
|
| 61:33 | and the slope, I mean the the gradient and the curvature coefficient, |
|
| 61:40 | can regard those as uh observables. we're not really interested in those, |
|
| 61:46 | really interested in the jump in VP the jump in vs and the jump |
|
| 61:51 | density. And so we can derive quantities by using these same chain rule |
|
| 61:58 | that we had before and we, , when we come to this. |
|
| 62:03 | so, um, that looks doesn't it? Um, uh, |
|
| 62:10 | we have same three quantities and we , uh, 33 observables are zero |
|
| 62:18 | two and are four and we have things that we're, uh, we're |
|
| 62:23 | interested in these three simple property jumps here. Uh, but, and |
|
| 62:29 | difficult in practice because this quantity the curvature is determined worse. That |
|
| 62:38 | if, if you look at real , you can usually find the normal |
|
| 62:44 | reflectivity is uh um uh pretty well with pretty uh a good um uh |
|
| 62:53 | . The gradient is not so but often it's good enough. But |
|
| 62:57 | curvature is usually very poorly determined. is the way seismic data is. |
|
| 63:04 | we can talk more about the reasons that if you like. But this |
|
| 63:07 | the one we wanna know most, this is the one that we measure |
|
| 63:13 | so that this is not good to the quantity the, the jumping VP |
|
| 63:17 | we're really most interested in depends upon observable, which is as the |
|
| 63:26 | Er so the best determined uh uh is usually the intercept and the grading |
|
| 63:37 | frequently determined. No, because of , most Avio analysis relies only on |
|
| 63:50 | intercept and the gradient and most of ignores this altogether. So uh we'll |
|
| 63:57 | later about is, is that a idea or not? But anyway, |
|
| 64:02 | Avio analysis that you have ever Olick discusses these two items. |
|
| 64:18 | what this says is that we don't have three observables because the seismic trace |
|
| 64:25 | an unknown scale factor in it. talked about this before. Uh seismic |
|
| 64:30 | are usually between plus or minus 1000 the reflectivity usually lie between uh plus |
|
| 64:36 | minus uh uh uh 10%. So all you can determine are ratios such |
|
| 64:43 | the ratio of the gradient to the and often that can be done pretty |
|
| 64:50 | . And this ratio here is uh done with great uncertainty. Usually we |
|
| 64:55 | even do that at all. So what we only think about is the |
|
| 65:00 | of the gradient term to the intercept . So we only have one reliable |
|
| 65:13 | , which is the relative value of two. Now, at this |
|
| 65:19 | we should recognize, yeah. Uh we analyze our motivations, we really |
|
| 65:29 | want to find things like Delta Mio or Delta VP over VP, what |
|
| 65:34 | really want to do is find So are there ways to um use |
|
| 65:43 | TV O analysis to find out? the answer is yes. Uh uh |
|
| 65:49 | for sure. And here's our secret is that high hydrocarbons, oil and |
|
| 65:59 | doesn't occur everywhere in the subsurface only places which are anomalous. So we |
|
| 66:07 | use a vo to find the So by this indirect way, |
|
| 66:13 | we're gonna show an analysis using a and we're gonna find a vo anomaly |
|
| 66:21 | we're gonna say these things are likely due to oil present when we found |
|
| 66:28 | anomaly in the subsurface from a vo likely to be anomalous fluids in that |
|
| 66:36 | , likely to be oil or And so, um, uh, |
|
| 66:44 | is a good time for me to and tell you another story from my |
|
| 66:51 | history. I am the inventor from Amao of a vo I was the |
|
| 66:58 | one who ever did it and um yet I'm not so uh proud of |
|
| 67:08 | , you know, Amaco and DP , and everybody has found an awful |
|
| 67:12 | of oil and gas using a VO I invented it for Amaco. I'm |
|
| 67:18 | particularly proud of that. And here's reason why, tell you this |
|
| 67:23 | I joined Amaco Research, I think 1979 and I came from a university |
|
| 67:34 | where I had been a geophysicist studying deep interior of the earth. And |
|
| 67:40 | knew nothing about the or they hired anyway because uh um uh uh the |
|
| 67:50 | our business was booming and they were anybody. They, they could |
|
| 67:54 | who knew how to spell your I knew how to spell it. |
|
| 67:58 | they hired me, I was an , I was an associate professor uh |
|
| 68:04 | State University of New York. So come to Tulsa and they said, |
|
| 68:10 | , so what are we gonna do this guy? And he looks like |
|
| 68:13 | maybe smart, but he doesn't know . And so while they're thinking about |
|
| 68:18 | they should do with me, my gets a phone call and the phone |
|
| 68:25 | comes from his um counterpart at the office in New Orleans. And this |
|
| 68:36 | the story that that guy that uh , uh low level boss and the |
|
| 68:41 | tells to my boss, he said we are partners uh with um uh |
|
| 68:52 | in a uh track offshore Gulf of . Mobile is the operating partner and |
|
| 68:59 | are the supporting partner, the only partner. He says yesterday Mobile called |
|
| 69:05 | partners meeting to discuss the current state the processing of this data set. |
|
| 69:14 | imagine this is 1980 and uh uh just beginning to explore offshore Gulf of |
|
| 69:24 | . We have um um a single behind our, our uh source boats |
|
| 69:31 | the single streamers are about three kilometers . None of this multis streamer 10 |
|
| 69:40 | business that that all came later. is early days of um oh marine |
|
| 69:52 | in the Gulf of Mexico two D only. We, we didn't dream |
|
| 69:57 | 3d in those days, only two seismic. And uh the state of |
|
| 70:03 | art was um imaging was uh uh uh Dick's uh velocity determination and move |
|
| 70:13 | removal and stacking. That was that it pretty primitive compared to what we |
|
| 70:20 | today. Uh And, and yesterday , and what uh what we do |
|
| 70:27 | is much more elaborate, but uh get much better images but, you |
|
| 70:33 | , in the Gulf of Mexico, in the subs salt, those techniques |
|
| 70:37 | pretty good. Those were really good for uh uh to find a lot |
|
| 70:43 | oil in the shallow subsurface in the of Mexico. So in those |
|
| 70:51 | most oil companies did most seismic data in house today. Uh Most of |
|
| 70:59 | is done in uh our uh arsenal uh contractor offices. But in those |
|
| 71:05 | , most of them were done in . So this was since Mobile was |
|
| 71:12 | operating partner, they were doing the . And the mobile guy calls up |
|
| 71:20 | buddy at Hamer car and says, uh come along and uh uh let's |
|
| 71:25 | at the uh at the current state imaging of our prospect, probably um |
|
| 71:32 | had 60% and we had 40% something that. I don't know. |
|
| 71:37 | they were the operating partner. They during the imaging. So our men |
|
| 71:43 | uh the these guys are friends. they've been working on this pro prospect |
|
| 71:48 | a few months and they've been friends that. And so our man walks |
|
| 71:53 | the street in New Orleans and they a cup of coffee and it's um |
|
| 71:58 | exchange some gossip and then the mobile says, let's look at the |
|
| 72:03 | So in those days, this was we had workstations on computers. And |
|
| 72:10 | the way we would do processing is would do the processing in a computer |
|
| 72:16 | they would print out the results on and then uh uh to look at |
|
| 72:22 | would spread the paper out on tables every oil company had lots of table |
|
| 72:29 | for spreading out paper sections. And think it was the early days of |
|
| 72:35 | color plotting. So, so uh that was a big deal that we |
|
| 72:43 | be. Uh we could plot uh could plot our, our images on |
|
| 72:49 | in color. Wow. And so uh the bong spreads out on the |
|
| 72:57 | , spreads out AAA sheet, you , maybe uh uh uh 3 ft |
|
| 73:03 | and uh 5 ft long, something that on the table. And they |
|
| 73:07 | lean over the table and look at . He says this is our prospect |
|
| 73:10 | then he points to the prospect and know, it's a fuzzy image and |
|
| 73:17 | he takes another sheet and he rolls out and he says this is the |
|
| 73:22 | diagram showing the sheer wave properties. , you know that uh the uh |
|
| 73:30 | the French painter in the 19th century Monet. He was an AAA pressure |
|
| 73:37 | a painter in the impressionist period of painting. He wrote his spreads |
|
| 73:47 | He says, here's the Monet diagram the marine showing the shear wave |
|
| 73:52 | This is Maroon data. Our man that there are no shear waves arriving |
|
| 73:58 | these dear phones. So his jaw and he sees this um uh so-called |
|
| 74:06 | diagram sh so called Marie uh uh properties the mobile guy sees the Amaco |
|
| 74:16 | drop and he realizes that he has displayed to Amoco some proprietary mobile |
|
| 74:27 | So he, he quickly makes an , rolls up the uh uh Monet |
|
| 74:34 | and sticks it aside and he oh, my mistake, this is |
|
| 74:37 | else. And so then they go with their meeting following a standard agenda |
|
| 74:43 | Iron Man pretend it's no big But as soon as he gets out |
|
| 74:48 | that meeting, he finds a, pay telephone puts in his quarter and |
|
| 74:56 | uh calls his boss, which is , is only two blocks away and |
|
| 75:01 | in New Orleans. And he says guys in uh Mobile know how to |
|
| 75:06 | sheer wave properties out of marine So by that time, it's late |
|
| 75:14 | the afternoon in New Orleans. But thing Monday morning that your arm's boss |
|
| 75:20 | up my Tulsa boss and he we believe that Mobile knows how to |
|
| 75:26 | sheer wave properties out of uh uh data. So, um my boss |
|
| 75:39 | , OK, we we'll look into and he looks around at his |
|
| 75:42 | everybody on his staff is busy except this new kid Leon who hasn't, |
|
| 75:48 | uh just walked in the door. few days before. So he turns |
|
| 75:52 | project over to Leon. And so quickly figured out everything that we currently |
|
| 75:58 | about a bo it's not hard, all spelled out in the uh uh |
|
| 76:05 | spelled out, for example, in the textbook, Ay and |
|
| 76:08 | it's spelled out there to um but in the context of oral uh uh |
|
| 76:19 | uh of oral exploration. So, uh uh so very quickly, we |
|
| 76:28 | that if you do an a vo , not only do you find uh |
|
| 76:34 | sheer property, but more importantly, find oil, you find fluid property |
|
| 76:43 | that's dynamite. That is direct detection hydrocarbons. Whereas before this, when |
|
| 76:50 | only looking at arrival times and making , you're looking at what you're doing |
|
| 76:55 | finding the configuration of the subsurface layer where it makes a dome, then |
|
| 77:02 | uh in the subsurface, maybe there's accumulated inside that dome. But you |
|
| 77:07 | know for sure that's called indirect exploration oil. But here we have a |
|
| 77:14 | attribute something you can compute uh from scientic data giving you the presence of |
|
| 77:24 | uh directly dynamite. So, uh soon as we realize this, we |
|
| 77:31 | a team of experts who went uh site and looked at a bunch of |
|
| 77:35 | AMACO data from the Gulf of Mexico we had uh uh uh drilled and |
|
| 77:41 | of them were successful wells and some them were not. And we looked |
|
| 77:45 | we found that where we had in found oil looking at that data, |
|
| 77:53 | found this attribute in the data which now call positive A vo and where |
|
| 78:00 | um um drilled a dry hole, data didn't have positive radio. So |
|
| 78:07 | , this new attribute that we didn't about at the time, we were |
|
| 78:11 | these holes. This new attribute would us avoid drilling dry holes. We |
|
| 78:17 | have positive a wouldn't drill. So immediately as soon as they came |
|
| 78:25 | from their off-site um uh operation, secret off-site operation, they came back |
|
| 78:33 | this news that uh uh not 100% with high probability, the presence of |
|
| 78:39 | A vo attribute was a good indicator if you drill there, you'll find |
|
| 78:44 | . So immediately I became clear that to Amaco management, that this is |
|
| 78:50 | important a topic to be left in hands of this new kid Leon. |
|
| 78:55 | they took it out of my hands gave it to an experienced researcher. |
|
| 79:02 | as one result of that, they no further progress in the theory for |
|
| 79:06 | next 30 years, I'll tell you about that story later. What next |
|
| 79:17 | wanna show you um how we can this idea showing here on the bottom |
|
| 79:21 | the screen, find anomalies with Ireland though we have all the difficulties which |
|
| 79:33 | have mentioned in the previous five OK. So let's consider only the |
|
| 79:40 | and the gradient. So these are two expressions and we're gonna consider this |
|
| 79:45 | normal segmental interfaces which have brine in pore space on both sides of the |
|
| 79:51 | . And then we're gonna also uh consider the other limiting case where we |
|
| 79:55 | brine on one side. And in pore space on the other side, |
|
| 79:59 | have gas well, OK. So the first case for the normal |
|
| 80:07 | uh here's our two expressions and uh know from lab data that normally, |
|
| 80:13 | this case, uh this term dominates . So thi this term here is |
|
| 80:19 | bigger than this one. And we that from uh lots of lab |
|
| 80:28 | And because of that, the gradient uh the gradient term has algebraic sine |
|
| 80:34 | to R zero. So, uh of this minus sign here, um |
|
| 80:40 | let, let me back up a this term here, the uh |
|
| 80:44 | the jump in VP is gonna have same uh algebraic sign as the jump |
|
| 80:49 | impedes usually. But uh uh whether positive or negative, it's gonna have |
|
| 80:55 | same sign. But because of this sign, it's normally true that the |
|
| 81:00 | uh term has an algebraic sign opposite the innocent. However, for the |
|
| 81:08 | case for Brian gas interfaces, we that this term is gonna be so |
|
| 81:13 | brian gas interface and let's assume that lithology is the same on both |
|
| 81:18 | The only difference is due to the , that's a useful limiting case to |
|
| 81:24 | of. Uh and the real case have also mythology differences on both |
|
| 81:29 | But for now, let's think of is the same on both sides, |
|
| 81:33 | differences in flutes. And in that , we will learn in lesson eight |
|
| 81:38 | to us by Mr B as he us about poor eas in that |
|
| 81:44 | this term is zero and sheer modulus not affected by uh by the type |
|
| 81:52 | fluid. So in that case, gradient term has the uh has the |
|
| 82:02 | um uh algebraic sign from here as . So the right there is the |
|
| 82:13 | of the idea of a bo and more complications that we've learned about a |
|
| 82:18 | about that since. But, but one, you, you can see |
|
| 82:22 | from what we've already done that uh where you have a fluid difference across |
|
| 82:29 | interface. That means that this term gonna be uh uh zero or |
|
| 82:35 | And this term is gonna have the algebraic sign positive or negative depending on |
|
| 82:40 | else is happening at the interface, as this one. So uh now |
|
| 82:45 | real world is gonna be more complicated both uh with many things changes. |
|
| 82:50 | example, it might have uh oil one side instead of rice. For |
|
| 82:54 | , you might have different Ortho on sides. But let's use these |
|
| 83:01 | the guide to guide our analysis looking anomalies. We're not gonna, we're |
|
| 83:11 | gonna uh um take these actual numbers seriously. We're gonna look for |
|
| 83:18 | OK. So here is uh some data um uh uh displayed within a |
|
| 83:27 | package uh uh run by BP. this is pretty old by now. |
|
| 83:32 | would say that probably BP has a uh better software now than it did |
|
| 83:39 | . But this was one of the that we put together. And I |
|
| 83:43 | remember whether this one was written by or by BP. Um Remember BP |
|
| 83:50 | Amaco in uh 1999 and all of first action with A VL was about |
|
| 84:00 | 1980 about 20 years earlier. So think this was first written in |
|
| 84:06 | Now look to see what we have . We have on the left, |
|
| 84:09 | have a seismic session and it's got uh it shows um uh uh an |
|
| 84:16 | in here with uh um this is bright spot. Uh Let me uh |
|
| 84:22 | me expand on that idea. We said the word bright spot before. |
|
| 84:30 | is an image. You don't see uh uh a vo behavior in |
|
| 84:35 | you see stacked amplitudes. And so is a, a place where the |
|
| 84:40 | are especially loud and so you could especially bright. So this was this |
|
| 84:46 | called a bright spot. And in , my father invented bright spots for |
|
| 84:53 | back in the 19 forties. So spot technology is the on looking for |
|
| 85:05 | places with fluids in them, anomalous , you know, hydrocarbons using the |
|
| 85:10 | amplitudes where a VO is doing the thing using prestack APLS. So back |
|
| 85:17 | my father did his invention of, bright spots, uh the A vo |
|
| 85:23 | was not feasible, but uh by 19 eighties, it was feasible. |
|
| 85:31 | so, uh let's just look at two D seismic section with a bright |
|
| 85:36 | in it and we look at that spot and we wonder is that due |
|
| 85:40 | anomalous fluids or maybe something else. , when the uh analyst first pulls |
|
| 85:47 | this data set, of course, no data at all. And then |
|
| 85:50 | , as he associates the uh the the, the seismic data previously computed |
|
| 85:56 | all and, and uh with this and then this thing shows up on |
|
| 86:02 | left uh and um uh and no here, no yellows, no |
|
| 86:11 | no greens, no, not just and white. And then um uh |
|
| 86:17 | the right here, yes, cross of intercept and uh slope. So |
|
| 86:27 | the intercept uh uh on this axis the slope or the gradient on this |
|
| 86:33 | . And when the um uh analyst pulls this up, uh there are |
|
| 86:38 | data showing here, all blanks just a blank spot waiting to be |
|
| 86:42 | in and no colors over here. the first thing that uh analyst does |
|
| 86:49 | he um uh oops Ferine, the does is to draw this yellow box |
|
| 87:04 | the bright spot. And as soon he does that, the software goes |
|
| 87:10 | at every position here and finds the which is lying behind this image. |
|
| 87:17 | in the gather, he's can calculate intercept and slow for every gather everywhere |
|
| 87:25 | here. But he, he, only looking inside the yellow box. |
|
| 87:29 | so when, as soon as he drawing the box, clicks the |
|
| 87:33 | all these points turn on and at point, they are all yellow. |
|
| 87:38 | you see a diff diffuse cloud of points. OK? Now, the |
|
| 87:44 | goes in and he draws the green where according to his uh expert |
|
| 87:54 | understanding there are no harder carbons inside green box. And so then he |
|
| 88:02 | the button. And what happens is some of these yellow, some of |
|
| 88:09 | yellow points turn green and they always a tight green cloud in the middle |
|
| 88:16 | the diffuse yellow cloud and the cloud has a negative slope good and it's |
|
| 88:24 | it's going down this way, never down this way, always a, |
|
| 88:29 | an elongated cloud with a negative And so what that means is that |
|
| 88:35 | gradient has the opposite side in the because it has this negative slope. |
|
| 88:42 | it has uh R two is positive zero is negative. So that's what |
|
| 88:46 | found isn't it uh a couple slides , we found that where there's only |
|
| 88:52 | differences across that reflecting uh horizon, you're gonna get a reflectivity uh where |
|
| 89:02 | uh um the gradient has the opposite from the intercept. Now, remember |
|
| 89:08 | is not reflectivity, this is received . So if you put a mouse |
|
| 89:15 | any one of these amplitudes, it's come back with AAA value between plus |
|
| 89:19 | and a minus 1000. These numbers are changing between plus and minus without |
|
| 89:25 | . So, you know that these really not reflectivity numbers, but we're |
|
| 89:31 | by the theory uh uh uh to uh look in the receive altitudes for |
|
| 89:39 | features that we understand should be in reflectivity according to our uh uh understanding |
|
| 89:49 | the effects of fluids on the Now, at this point, he's |
|
| 89:54 | um a diffuse yellow cloud with a green cloud in here with a negative |
|
| 90:03 | . He notices there's lots of yellow outside the green cloud. Where do |
|
| 90:09 | come from? They, they do come from inside the green co inside |
|
| 90:14 | green box. They come from somewhere . He wonders to himself, where |
|
| 90:19 | those oh, anomalous points come from the section? So, um on |
|
| 90:28 | cross spot, then he he, um isolates with a cross plot uh |
|
| 90:36 | points here on uh uh uh on side of green cloud. And as |
|
| 90:43 | as he isolates those points maybe with ellipse or something. Uh uh Then |
|
| 90:50 | looks over here to see where those from and look, they come from |
|
| 90:54 | top of the structure. That's where buoyant fluid might collect. What we've |
|
| 91:04 | is where the uh the intercepting so have the same um same algebraic |
|
| 91:11 | . That's this quadrant. Here we , has the same, those points |
|
| 91:15 | from the top of the structure. not. No, it's a |
|
| 91:23 | it's a pattern. Uh uh uh these points, you don't know when |
|
| 91:27 | look here, you don't know where came from. But uh uh over |
|
| 91:31 | , you see where they came they came from the top of the |
|
| 91:35 | where buoyant fluids might um might Now, the only uh uh fingered |
|
| 91:46 | here uh in, in uh with in the third quadrant where interception ingredient |
|
| 91:51 | the same slope because he was uh guided by uh um uh some uh |
|
| 91:57 | that says that uh that's called a two anomaly. However, you see |
|
| 92:03 | the anomalous points are scattered all around . So probably these are coming from |
|
| 92:10 | same anomaly here. He just didn't them uh because he was uh his |
|
| 92:15 | was uh dominated by uh uh other thinking. And furthermore, these points |
|
| 92:24 | here, they probably came from the of the enough. But this one |
|
| 92:30 | here is the essential information that we that we uh need to know that |
|
| 92:36 | anomalous points in the cross block correspond the top of the structure in the |
|
| 92:44 | . So what we have done here we have been guided by a very |
|
| 92:50 | theory, ignoring all the uh you , treating received amplitudes as though they |
|
| 92:56 | reflectivity. We know that's wrong. we were guided by that theory. |
|
| 93:00 | have been able to empirically locate anomalous in the earth. Wow. Look |
|
| 93:06 | that. It's not certain, but does substantially lower the risk for drilling |
|
| 93:10 | dry hole. Wow. So now call this the qualitative a VO program |
|
| 93:20 | it often works. In fact, has been responsible for finding lots and |
|
| 93:23 | of oil for many countries all over world, many companies all over the |
|
| 93:30 | . However, there are many instances what is called anomalous A bo behavior |
|
| 93:34 | cannot be properly explained in these But I would say that qualitative A |
|
| 93:46 | has been a fabulous success for the industry over the past 40 years. |
|
| 93:57 | you gotta ask uh uh why don't do this quantitatively, you know, |
|
| 94:04 | numbers instead of just using patterns Uh so that's what we call the |
|
| 94:13 | a VO program. And quantitatively, can see there is a problem. |
|
| 94:18 | at this litho theological slope. It a slope of about a minus |
|
| 94:26 | It is, it goes down about units for every one unit uh uh |
|
| 94:31 | line we expect from laboratory data, expect a AAA uh a negative slope |
|
| 94:41 | about a minus one. So you see that uh all the mistakes that |
|
| 94:46 | made here in treating them received amplitudes reflectivity. They, they are uh |
|
| 94:53 | up in this way in this So to correct for all those, |
|
| 95:00 | I went back uh so to correct uh to correct these received amplitudes in |
|
| 95:06 | reflectivity, we do not know how do this. And I don't think |
|
| 95:12 | will ever learn how to do that for all the other effects. But |
|
| 95:19 | me show you a way to correct all of them easily the zero effort |
|
| 95:29 | facilities provided to us by Mr Bill . You take this image right here |
|
| 95:37 | you grab the image with your mouse push it up and press it |
|
| 95:42 | So when you do that compressors up that, now the slope has the |
|
| 95:52 | value about minus one about that data by powerpoint. Well finding via |
|
| 96:02 | The important thing is that as we've this image, we've changed the scale |
|
| 96:09 | the uh gradient with respect to the , we left the intercept unchanged and |
|
| 96:16 | uh and we scaled the gradient, , the anomalies are still anomalous and |
|
| 96:22 | still come from the top of the . So what we've done is we've |
|
| 96:29 | a way we found a workflow which for many of our mistakes. Uh |
|
| 96:38 | uh still finds or fantastic. maybe if we had a more serious |
|
| 96:57 | for quantitative a vo we might even , might be able to do even |
|
| 97:04 | than we've done with a vo for past 40 years in, in this |
|
| 97:09 | . What we have to do is learn how to correct for propagation effects |
|
| 97:13 | we also have to call it uh for anisotropy. Um Tell you then |
|
| 97:22 | , the ending of the story uh the, the next step in the |
|
| 97:25 | that I told you about my personal of a VO cam, I said |
|
| 97:37 | took as soon as we found out valuable a vo can be for finding |
|
| 97:43 | , they took the project out of hands. But I thought, you |
|
| 97:52 | , um maybe we can do better about what we're doing. We're examining |
|
| 98:01 | angular beh the, the, the of amplitudes on offset. That means |
|
| 98:08 | examining the dependence of attitudes on incident . But we're doing all of our |
|
| 98:17 | in terms of isotropic medium. We're we're ignoring the possibility of velocity variation |
|
| 98:25 | velocity A VO without VVO. Does make sense? And so I thought |
|
| 98:33 | it, even though the project was of my hands, I thought about |
|
| 98:37 | answer uh of the, of that . Uh um Anyway, and I |
|
| 98:45 | to the conclusion that uh uh uh should be analyzing our a our amplitude |
|
| 98:54 | using uh concluding the effects of velocity of all set ie including anisotropy, |
|
| 99:04 | we're not yet ready to talk about until we've gotten some ideas from anti |
|
| 99:10 | in luxury tent. OK. So have, we, we now know |
|
| 99:20 | to find oil and gas using a . Basically, we're finding Avio anomalies |
|
| 99:29 | we're finding them with a workflow which a lot of simplifications, but it |
|
| 99:34 | anomalies. And when we drill only anomalies, we drill through a dry |
|
| 99:43 | . Now, this attribute that we're , that's an attribute. It's a |
|
| 99:48 | of the interface. It depends on ZP. It depends upon delta |
|
| 99:55 | It depends upon delta. It doesn't upon Z or, or V or |
|
| 100:00 | itself only across depends on the, jumps across the reflecting horizon. So |
|
| 100:09 | people, many of our colleagues really it easier to think about layer |
|
| 100:14 | They'd rather think about uh uh uh uh layers of high impedance rather than |
|
| 100:20 | with impedance jumps. So these layer can be computed from the interface properties |
|
| 100:28 | we talked about already. And we that computation seismic inversion. So you |
|
| 100:36 | learn more about seismic inversion in a devoted to a VO So everything that |
|
| 100:41 | learn here will apply to those computer properties. Now, I think that |
|
| 100:47 | will have a course in a VO uh later in this sequence. Uh |
|
| 100:53 | Utah. Are you gonna be the the T A for vacation? |
|
| 100:59 | uh, the A O? Yeah. Ok. So, in |
|
| 101:04 | course, I, I don't know gonna be teaching that course. It |
|
| 101:07 | be, uh, Kana, could be Kana or it could be |
|
| 101:12 | else. And so you will learn that course, uh, um, |
|
| 101:19 | that, uh, uh, are what I'm telling you in this |
|
| 101:24 | So, what you should do uh, uh, um, |
|
| 101:29 | ask questions and you'll say, uh Professor Thompson taught us, |
|
| 101:34 | told us this and uh uh it's what you're telling us. Uh could |
|
| 101:39 | um explain the difference? Oh, , it might be uh Hiltermann, |
|
| 101:45 | uh is also an expert in, AVI O and so that way you |
|
| 101:49 | a, a constructive uh uh discussion between you and uh that instructor and |
|
| 101:57 | colleagues and everybody learns from these kinds challenges. Ok. Oh, you've |
|
| 102:10 | had ultimate squash. Are you the A? Oh, ok. So |
|
| 102:15 | , in Hiltermann, of course, probably learned stuff that uh um uh |
|
| 102:22 | uh contradicting to, uh, to I have said and I will tell |
|
| 102:27 | more which is contradicting to what that course said. Uh, it uh |
|
| 102:33 | a student, you should be concerned uh inconsistencies between what your various professors |
|
| 102:41 | you and you should feel free uh um uh uh ask questions either |
|
| 102:50 | my course or in uh uh the course, by the way, this |
|
| 102:55 | in um uh waves and waves. should have been your first course because |
|
| 103:02 | else that you, you do in geophysics relies on what you're learning in |
|
| 103:07 | course. So it should have been first course. But for various practical |
|
| 103:12 | , we couldn't arrange it this year uh uh be the first course. |
|
| 103:16 | so you, uh uh you're uh things out of order but it doesn't |
|
| 103:22 | uh uh for you to, think, uh, now you've already |
|
| 103:26 | Hiltermann course. Um, uh, , what about the, uh, |
|
| 103:35 | differences between, uh, uh, ideas that Hilman gave you and the |
|
| 103:43 | that Thompson has given you? um, uh, I'm happy |
|
| 103:48 | uh, answer any questions you might , uh, remember, uh, |
|
| 103:53 | we finish today, you are going , um, uh, go home |
|
| 103:59 | a week and I'll see you again Friday by that time. I hope |
|
| 104:04 | have a lot of questions that, , come from. You're comparing what |
|
| 104:11 | told you with what Hiltermann told And, uh, so we'll, |
|
| 104:16 | , dis discuss them, then I'll you, uh, my answers to |
|
| 104:21 | questions. And if you feel like , you might wanna go to Professor |
|
| 104:26 | and say, uh, um, , um, I'm confused. This |
|
| 104:32 | what you said. This is what said. Uh, can you help |
|
| 104:35 | out? Uh Hiltermann will be happy engage you in that kind of |
|
| 104:43 | So, um, let us, , uh, leave this topic uh |
|
| 104:50 | this point and we have a little . Uh uh So I think that |
|
| 104:59 | Carlos, I think you're up um true or false. Is this statement |
|
| 105:03 | or false? It says in a reflection point, gather the conversions of |
|
| 105:09 | to angles requires an accurate estimate of velocity both above and below the reflecting |
|
| 105:17 | . Is that true? Her I think it's true professor. Uh |
|
| 105:27 | . So uh uh there's two parts . Yeah, you can do it |
|
| 105:32 | using the offset data. But uh mean if you want to have the |
|
| 105:37 | position of the sack angle, you need uh uh uh an accurate velocity |
|
| 105:45 | for the layers that what do you ? Do you need that accurate velocity |
|
| 105:51 | below the reflecting interface? Or would be happy if you only had it |
|
| 105:57 | ? OK. Mhm I, I think about this. It's |
|
| 106:04 | Yeah. Yeah. Yeah. So statement is false because all we need |
|
| 106:10 | the velocity information above. OK. . Thank you. Yeah, I'm |
|
| 106:17 | reading, I'm not reading the the question. Uh Yeah. OK. |
|
| 106:24 | uh Rosa this one is for it Avio analysis is best done on migrated |
|
| 106:31 | gathers that is true. Well, do you remember we talked about the |
|
| 106:45 | of migration on amplitudes. Uh What I'm thinking is that um some um |
|
| 106:56 | algorithms might mess up the amplitudes. it would depend on the migration. |
|
| 107:03 | it's a maybe that's right. So , my best answer here is that |
|
| 107:08 | uh uh and the way you find of course is you ask your expert |
|
| 107:12 | you say uh uh uh if I your algorithm, what is it doing |
|
| 107:18 | my amplitudes? He should know the by the way. Uh But, |
|
| 107:23 | professor then uh yeah, it's going depend on the algorithm, but they |
|
| 107:28 | is going to depend on the geology I mean, if the, if |
|
| 107:32 | beds are dipping with a high yeah, the, the amplitudes are |
|
| 107:38 | going to be in the current So you are not going to be |
|
| 107:41 | to use for interpretation of the So, yeah, so, uh |
|
| 107:45 | , II, I think that's a point uh depending on the subs services |
|
| 107:49 | . So, um um uh I think the answer here is uh |
|
| 107:56 | , the right answer is that maybe on all those things. Uh So |
|
| 108:04 | um le le how about this? says uh uh look at the |
|
| 108:09 | we got ABC D and then all the above. And so let's uh |
|
| 108:14 | gonna uh uh uh I, I'm going to um uh OK. |
|
| 108:25 | I'm gonna ask you, Lili uh you're saying what B is the gradient |
|
| 108:32 | , not both of the above and all of the above, but the |
|
| 108:36 | . Yes. So, uh uh I'm gonna uh uh call that |
|
| 108:41 | that's the correct answer. However, about this in the velocity uh in |
|
| 108:49 | the impedes, you know, the term has only impedance inside the impedance |
|
| 108:54 | the P wave velocity inside the P velocity is kra plus four third |
|
| 109:01 | So uh would you say that if measure the intercept, it uh does |
|
| 109:08 | sheer wave properties appear in the Because of what I just said, |
|
| 109:19 | know, since the shear wave property the intercept is only occurring in the |
|
| 109:25 | K plus four thirds mu uh uh in that combination, not by |
|
| 109:31 | but only in that combination. That's P wave combination, a plus four |
|
| 109:35 | mir. And so we gave that name M and uh so that's a |
|
| 109:40 | wave property, not a sheer wave . Uh When we say P |
|
| 109:45 | we really should be saying longitudinal waves inside of a P wave, it's |
|
| 109:50 | a pure pressure inside that pulse. a longitudinal stress. So we should |
|
| 109:56 | them longitudinal waves. But you everybody says P waves. So we |
|
| 110:00 | as well go along a, along that. We remember that in A |
|
| 110:03 | wave, the stress is longitudinal. it's got some uh uh some sheer |
|
| 110:13 | inside that longitudinal stress. But your is correct. It's only in the |
|
| 110:17 | term. OK. So Carl, uh back to you um now true |
|
| 110:27 | false, the gradient term may be in terms of porcelain's ratio. Although |
|
| 110:33 | expression is either more complicated or it more assumptions. Is that statement to |
|
| 110:40 | fault? 729. Mhm. I to hear you thinking like a |
|
| 110:51 | I don't, I don't, I remember saying that. Yeah, I'm |
|
| 110:55 | sure professor. OK. So uh the way uh if a question like |
|
| 111:00 | appeared on the exam, you'd have problem, you just go back and |
|
| 111:05 | it up. Uh uh So uh now, I think it's true, |
|
| 111:10 | . Yeah. Yeah. So uh you are correct. That's true. |
|
| 111:19 | . So Brisa uh says true or . Is it easy to estimate the |
|
| 111:25 | property jumps at the interface by a algebraic combination of the Avio intercept and |
|
| 111:32 | is that easy? No, it's . It, yeah, it's false |
|
| 111:38 | it's not, you can do but it's not easy because it involves |
|
| 111:42 | curvature which is uncertain. Yeah. , good answer. OK. Um |
|
| 111:50 | late it says that the relation between intercept and graded depends among other things |
|
| 111:59 | whether or not the fluid content changes the interface, true or false. |
|
| 112:07 | didn't hear you in the past. Well. OK. So um how |
|
| 112:15 | you grow? Mhm OK. Um looked at a case specifically uh uh |
|
| 112:23 | Brian gas case. There's a case the food content was different across the |
|
| 112:28 | . And we found out that in case, the relation between these two |
|
| 112:33 | uh depended on that food content. I'm gonna say that this uh this |
|
| 112:39 | is mhm OK. So, um uh let's go on to think about |
|
| 112:51 | special cases. So how about at free service? Now, normally the |
|
| 112:59 | surface is that particular interface which reflects most energy. And of course, |
|
| 113:04 | reason for that is at the free on one side, you have a |
|
| 113:09 | or maybe water and on the other you got air. So there's a |
|
| 113:13 | contrast there. So, what that is that there's uh uh uh uh |
|
| 113:20 | the biggest reflection. Excuse me? we have a very quick break? |
|
| 113:30 | OK. So, uh, as matter of fact, thank you for |
|
| 113:33 | . Uh, this is now a time for a break. So let's |
|
| 113:36 | back here and stop right here. , I lost track of time. |
|
| 113:42 | let's stop here and pick up in minutes. Uh, um, uh |
|
| 113:47 | point we have over here. Do have everybody here? Um, |
|
| 113:54 | are you here, Bria? Are here? So I think maybe we'll |
|
| 114:08 | till we. Uh, so we them. Oh, here's Carlos and |
|
| 114:22 | , uh I'm sure that brace will here shortly. OK. So here |
|
| 115:43 | is. So, uh, then get started. And so, |
|
| 115:47 | this is our topic uh for uh , the next topic, uh, |
|
| 115:54 | at the free surface. So, we said, uh, the free |
|
| 116:01 | is normally the one that generates the uh uh uh energy. Uh uh |
|
| 116:07 | also generates what we call surface related . So we haven't talked about multiples |
|
| 116:13 | all. Uh Yet, we'll talk those more in lecture seven, which |
|
| 116:20 | uh uh the next lecture next So I'm gonna skip that for |
|
| 116:26 | And uh uh uh point out that the free surface is uh uh in |
|
| 116:34 | marine context, that's at sea, we have a source ghosts and receiver |
|
| 116:41 | . So our source go ha source happens because we tow the source in |
|
| 116:48 | marine survey, we tow the source few meters below the surface, maybe |
|
| 116:55 | or 10 m below the surface depending uh a number of things which uh |
|
| 117:01 | the operator decides. And so when uh source uh goes off, we |
|
| 117:08 | before here. Normally uh these the marine source is not dynamite, |
|
| 117:14 | an ergot or maybe an array of . And so the air gun emits |
|
| 117:21 | pulse of high energy of compressed air the water and then that makes a |
|
| 117:28 | and expands. And uh so that's few meters below the surface. Some |
|
| 117:34 | the energy from that uh excuse when, when it in, when |
|
| 117:39 | injects the air into the water that up sound waves both down and also |
|
| 117:47 | . So the sound waves that go , go up to the free surface |
|
| 117:51 | come back down and they follow along the direct arrivals which start off going |
|
| 117:58 | . And so we call that a . And uh so that's a AAA |
|
| 118:03 | delay multiple. And so on the end, the receiver, uh geophones |
|
| 118:09 | normally um towed a few meters below surface. Uh And so the, |
|
| 118:17 | the reflections coming up from below, of them hit the receivers directly and |
|
| 118:25 | of them go past the director, the receivers up to the free service |
|
| 118:31 | back down again. So that uh uh same two way travel time uh |
|
| 118:36 | above the uh receivers. Uh Usually a similar distance than uh the for |
|
| 118:43 | source goals. And so those are short delay multiples, but they're strong |
|
| 118:50 | they reflect off of the free Now, in the case where we |
|
| 118:58 | ocean bottom size receivers, normally, a case where they uh where the |
|
| 119:04 | uh is deep, it might be ft deep, it might be 1000 |
|
| 119:09 | deep, it might be 5000 ft . Uh But the uh the receivers |
|
| 119:14 | sitting down there because that um uh between the receiver and the free surface |
|
| 119:24 | so big. We have special techniques dealing with those. And now, |
|
| 119:29 | so I don't wanna talk about uh special techniques at this point. |
|
| 119:36 | here's something you might have thought Uh uh So uh we on |
|
| 119:41 | so we have on land, the are exactly at the surface. Uh |
|
| 119:47 | attached to the free surface probably with stake and they are uh uh uh |
|
| 119:52 | exactly at the free surface, but do not record the incoming w think |
|
| 120:00 | that, they record the incoming waves the outgoing waves at the same |
|
| 120:07 | So that's what we earlier called the with the free surface. Often we |
|
| 120:13 | think about that. Uh The uh receivers did not record the upcoming energy |
|
| 120:20 | . They recorded the upcoming energy and reflected energy which is not left |
|
| 120:28 | it hasn't left. So it's present the same time as the uh uh |
|
| 120:33 | upcoming uh uh wavelength and get suppose we're on land and suppose we |
|
| 120:43 | a AAA a AAA few 100 m offset or more the uh the incoming |
|
| 120:49 | is gonna be coming up at an . And so what that means is |
|
| 120:54 | a is it's uh as it interacts the free surface, it's gonna make |
|
| 121:00 | shear waves, converted reflected shear And those are present also. And |
|
| 121:06 | the instrument records is the sum of the incoming and the outgoing waves because |
|
| 121:13 | outgoing waves have not left yet at time of the recording it's all |
|
| 121:19 | So that's uh uh that's quite isn't it? So, because this |
|
| 121:31 | from the free service are strong not weak reflections. We can't use |
|
| 121:36 | linearized theory that we talked about before the uh uh we came up |
|
| 121:41 | the, the linearized a voe equation was for reflections, which resulted from |
|
| 121:52 | where the uh medium on both sides similar. But at the free |
|
| 121:57 | the medium on the one side is or water and on the other side |
|
| 122:01 | air. So uh that approximation is good. So now let's go back |
|
| 122:09 | to the exact expression which is exact uh uh for isotropic uh bodies. |
|
| 122:17 | we're gonna apply this uh free surface the free surface. The uh uh |
|
| 122:27 | upper medium, the reflecting medium has P velocity and it has zero sheer |
|
| 122:35 | and zero density. Now, because these quantities occur in the, in |
|
| 122:40 | denominator down here, we can't just them to zero. See, |
|
| 122:45 | we, here's the uh uh that , the velocity of the uh of |
|
| 122:54 | reflecting media. And now it's the the upper interface. It's, it's |
|
| 123:00 | , it's the, this is now velocity above the free surface. So |
|
| 123:06 | can't just put in a zero Instead, we, what we're gonna |
|
| 123:12 | is we're gonna consider the limiting behavior quantities like this approach zero. And |
|
| 123:19 | gonna find out that eventually we get zero divide by zero and we'll figure |
|
| 123:25 | what that means. So we do in the uh uh uh uh first |
|
| 123:30 | considering not zero V two but small two. OK. So, a |
|
| 123:39 | we do this, the first ones easy for. So let's look at |
|
| 123:43 | here. Oops and go back one , one more. So we got |
|
| 123:49 | these quantities here notation for all And, and so first we're gonna |
|
| 123:54 | at these and then we're gonna look these. OK. So first one's |
|
| 124:00 | . So for example, uh uh the quantity A this is the definition |
|
| 124:06 | in that definition, this term is . So this and this term is |
|
| 124:13 | small. So uh we can neglect of this in comparison with this. |
|
| 124:19 | that the A simplifies down to this here, which is just second |
|
| 124:25 | And in a similar way, these simplify as we've shown here uh for |
|
| 124:34 | next point assu assume that we have uh let's look at these um |
|
| 124:40 | So for example, cosine theta that's the, the angle of the |
|
| 124:45 | wave in the upper medium above the surface, that's one minus the sine |
|
| 124:51 | of the same angle. And so sine squared because of Snell's Law has |
|
| 124:56 | VP two in it, we would that's small. So that uh uh |
|
| 125:01 | term goes away, we have the root of one. So we, |
|
| 125:04 | gonna set cosine theta two equals one cosine theta four that's for the transmitted |
|
| 125:12 | converted S wave also a one. the next set of terms is almost |
|
| 125:21 | easy. Just uh uh uh extending we've already learned. Uh Or we're |
|
| 125:27 | find out that uh this quantity, example, uppercase E simplifies down to |
|
| 125:33 | over VP two. So why is VP two is small? And so |
|
| 125:40 | term is gonna be big compared to one. So even though we don't |
|
| 125:44 | VP 20, it's small and it's here. So this term dominates but |
|
| 125:51 | is a one. So this turns AC over VP two, see how |
|
| 125:56 | goes. Uh uh Because the small in the above the s uh free |
|
| 126:03 | is small, that means that this is gonna dominate. And it looks |
|
| 126:07 | we're gonna uh uh get infinity there zero here. But don't worry about |
|
| 126:11 | , eventually we're gonna come to zero by zero. OK. So similar |
|
| 126:17 | uh to uh uh uh to um you know, we, we |
|
| 126:22 | these simplifications and then finally, we to, to put it together um |
|
| 126:32 | And to make the quantity which we D and we uh and we find |
|
| 126:39 | combination, you see here, we a square of uh small quantities. |
|
| 126:44 | are the T velocity above the free and the sheer velocity above the free |
|
| 126:49 | . Uh It's uh uh both of are small. And so it looks |
|
| 126:56 | we're in big trouble here. Looks the D is gonna be a very |
|
| 127:00 | number because of these small numbers in uh uh denominator well, don't give |
|
| 127:09 | yet because what we have here, uh uh the reflection coefficient has in |
|
| 127:15 | one over D. And so when um uh uh simplify according to what |
|
| 127:22 | just learned, we, we still these small quantities here, but we |
|
| 127:27 | a one over D here. So gonna help a lot. And so |
|
| 127:32 | go through the uh the algebra and find uh uh uh going through the |
|
| 127:40 | here, you can follow along through for yourself later. And now we're |
|
| 127:43 | ask ourselves uh uh is this But remember we have a, a |
|
| 127:48 | over D here, the D had was also uh infinity. Uh You |
|
| 127:56 | , uh So those things are gonna out uh this product VP two times |
|
| 128:05 | two times D is uh uh go together and it comes out that |
|
| 128:10 | it's equal, it's this quantity in , not infinity. So these, |
|
| 128:16 | very small terms cancel out and we're with this thing which is not uh |
|
| 128:23 | small, not large, it's, know, it's a reasonable number. |
|
| 128:27 | because of all these considerations, the reflection coefficient exactly simplifies in this case |
|
| 128:36 | this expression here. Now look at expression um um yeah, the only |
|
| 128:46 | in these two in the numerator and denominator is in this algebraic sign right |
|
| 128:54 | , see that. So at normal , the ray parameter P is a |
|
| 129:03 | . So that's a zero and that's zero and this is one divided by |
|
| 129:08 | times the minus one. So that normal incident, um um uh you |
|
| 129:16 | , at the free surface uh that coefficient is a minus one. So |
|
| 129:23 | means that any wave which is coming gets reflected down completely. I, |
|
| 129:29 | think that makes sense. OK. that's a normal incidence. Now at |
|
| 129:35 | at oblique sense, uh there's gonna some other issues. So let's uh |
|
| 129:41 | uh deal with those uh shortly uh go through the same sort of logic |
|
| 129:48 | the converted wave coefficient. And uh this is what we start off with |
|
| 129:56 | f at the free surface it simplifies this and at normal instance is still |
|
| 130:02 | go to zero. Why is Oh yeah. At normal instance, |
|
| 130:07 | goes to zero because this quantity is zero here. Yeah, yeah. |
|
| 130:14 | this is gonna be AAA OK. I, I'm showing you that |
|
| 130:23 | the reflection and con and the conversion uh for any angle um uh for |
|
| 130:33 | angles, it's a little bit complicated you see here and as you saw |
|
| 130:37 | , for the reflection coefficient. But it's uh uh it's something we can |
|
| 130:44 | we can match. Excuse me, , I have a question. So |
|
| 130:50 | this mean that at normal incidents there not converted waves at the free |
|
| 130:58 | That's correct. That's what that, what um this says. Now, |
|
| 131:05 | we shouldn't necessarily, I think that's happen. Yeah, I think it's |
|
| 131:12 | be, um, I think it's be next week that I show you |
|
| 131:19 | data, actual data where that's not . And so, well, that's |
|
| 131:24 | puzzle. Uh uh uh I'm gonna you an actual data where we have |
|
| 131:34 | converted wave reflections at normal incidents even this says it's not possible. So |
|
| 131:42 | we look at that data, we're say uh oh, the data does |
|
| 131:46 | conform to the theory, what in theory could we possibly have done |
|
| 131:55 | So let's save that discussion until we at that data. Now, remember |
|
| 132:04 | I said, it said on the on land surface recorders record both the |
|
| 132:09 | wave and the reflected wave and the converted wave altogether. So we do |
|
| 132:19 | measure incident waves, we measure all it together. Now, for a |
|
| 132:27 | incident uh wave, this summer waves I just said here, this summer |
|
| 132:39 | is for us of the go back uh page 14 as we first started |
|
| 132:46 | about normal instance. And we uh , we find that uh uh uh |
|
| 133:12 | , yeah, when we first look normal incidence, we found this relationship |
|
| 133:17 | the, the uh the infinite and boundaries uh in incident and reflected |
|
| 133:23 | And so um uh uh uh um all this together and uh simplifying |
|
| 133:32 | we come to the uh this different uh incident minus reflected equals twice the |
|
| 133:41 | . Well, you know, this uh slide is not a very good |
|
| 133:47 | because it's got the incident amplitude on sides of this equation. What we |
|
| 133:53 | to do is take one more step . And that uh when we take |
|
| 133:57 | one more step, we're gonna find minus W one equals one times W |
|
| 134:04 | . So the, the amplitude of reflected wave is the negative of the |
|
| 134:10 | of the infinite wave. So this uh the uh the interaction of the |
|
| 134:16 | with the free service at normal And so this interaction was first mentioned |
|
| 134:22 | page 53. So I'm sorry, , I need to go back and |
|
| 134:26 | this up. Uh uh Here, had that one more line with the |
|
| 134:31 | manipulations. So the answer is So that's uh uh that's either on |
|
| 134:41 | or at sea at C. there's a further special case where the |
|
| 134:47 | uh where the sheer velocity in the be is zero, that's water. |
|
| 134:53 | , uh uh in that case, quantity D uh uh which we analyzed |
|
| 134:59 | that simplifies further to zero. And the reflection coefficient uh because D is |
|
| 135:10 | zero, that's a zero here and zero here. And so, uh |
|
| 135:15 | , in this case, at we find the incident, uh the |
|
| 135:19 | coefficient is minus one for all not just normal incident, but all |
|
| 135:27 | les and of course at sea we have uh uh zero converted waves |
|
| 135:34 | . So you can see how um need to treat the free surface differently |
|
| 135:40 | it's a strong reflector, not a reflector, but because of its special |
|
| 135:46 | , uh uh things simplify in a nice way. And you get uh |
|
| 135:52 | uh uh well, in the simplest at, at uh at sea, |
|
| 135:56 | gonna find the reflection coefficient or uh , is a minus one, all |
|
| 136:02 | angles. By the way, when we talked uh about converted waves |
|
| 136:12 | recording on ocean bottom seismometers, I uh we did that. Uh uh |
|
| 136:18 | , I said that with what we have ocean bottom receivers is we have |
|
| 136:23 | four component instrument that means three vector , vertical and two horizontals and also |
|
| 136:33 | hydro phone. So it makes a component receiver. Why do we have |
|
| 136:37 | four components? Well, the reason because there's a special techniques for combining |
|
| 136:45 | date, the signal from the hydrophone the signal from the vertebra geophones to |
|
| 136:52 | the water layer multiple. So that uh that operation depends strongly on this |
|
| 137:01 | that we've developed here later with reflection of, of that uh a water |
|
| 137:07 | multiple is a minus one, no what angle it comes up at. |
|
| 137:14 | also uh no matter what's the, the uh and no matter what's uh |
|
| 137:21 | properties of the sea floor, we're gonna get the combination of the uh |
|
| 137:27 | the um and not the incident medium the uh a water layer of in |
|
| 137:38 | primer and the water layer multiple are be nicely eliminated using that operation because |
|
| 137:47 | this minus one. So it's a , I think this one is due |
|
| 138:00 | Bria. OK. So uh to that uh what we have uh ABC |
|
| 138:06 | D it says on, at the service on land, the reflection coefficient |
|
| 138:13 | , would you leave? It's c uh she is from all angles. |
|
| 138:24 | We just proved that. Uh that's . I'm gonna back up one |
|
| 138:29 | So that's true at all angles. For uh this is for the marine |
|
| 138:34 | . OK. Yeah, this is the marine environment on land is not |
|
| 138:39 | . So uh we showed on land uh it was uh the uh |
|
| 138:45 | this minus one is true only for instance. So if we had said |
|
| 138:50 | a minus one instead of one, answer would have been a but uh |
|
| 138:56 | answer, but that's not what a a says plus one. So the |
|
| 139:00 | answer is none of the above. . OK. So um oh Le |
|
| 139:09 | um uh which of these is See, right? That's what we |
|
| 139:16 | showed, we just showed that, burger. OK. Now, so |
|
| 139:22 | of that seems pretty. Um I say that that probably that seems to |
|
| 139:30 | to be a um reasonable and something can uh uh uh useful, reasonable |
|
| 139:39 | useful ways to think about uh reflection data. And I, I would |
|
| 139:46 | with that. Uh But now I consider some complications. So fir first |
|
| 139:53 | we're gonna gonna be considering is the angle and what happens to waves at |
|
| 140:00 | at uh which are incident or the angle is beyond the critical angle. |
|
| 140:06 | . So uh this is repeating what said before that because of Snell's law |
|
| 140:12 | the transmitted P wave in certain P . Now, looking at the transmitted |
|
| 140:17 | wave, the transmission angle is given Snell's law here. And if this |
|
| 140:25 | is uh uh more than one and big enough, more than one, |
|
| 140:32 | you have for some angles uh theta , this product is more than |
|
| 140:38 | And so in those cases, uh sign of theta two is gonna be |
|
| 140:43 | than one, which makes a problem if the sign, if the sine |
|
| 140:52 | the angle is more than one, the cosine of the angle is |
|
| 140:56 | So uh uh the situation just begins get weird when uh uh when uh |
|
| 141:03 | the sign of the two is actually equal to one hasn't gotten, |
|
| 141:09 | I haven't looked at, at, uh uh angle uh incident angles big |
|
| 141:14 | to make it greater than one, exactly equal to one. And so |
|
| 141:18 | that angle, that's the definition of critical in infinite angle, which is |
|
| 141:26 | . So for example, if we uh VP one equals 2000 m per |
|
| 141:34 | and VP two equals 4000 m per , that ratio would be one half |
|
| 141:39 | the critical angle would be 30 Uh you know, S sin sin |
|
| 141:45 | 30 degrees is one half. normally we don't have such a big |
|
| 141:49 | between the uh uh infinite medium and reflecting medium. So normally the sine |
|
| 141:55 | uh normally the critical angle is a bigger angle, maybe 40 or 50 |
|
| 142:02 | 60 degrees. And so uh we have uh we frequently have those in |
|
| 142:07 | data, but only at shallow Normally, we design our max our |
|
| 142:15 | to have maximum offsets so that post angles do not occur in our data |
|
| 142:23 | the target reflector. But for shallower , we can have a larger |
|
| 142:32 | of course, for a shallower event the same maximum offset. The uh |
|
| 142:38 | angle is gonna be uh bigger and we could have most critical reflections. |
|
| 142:49 | , at post critical angles, we have Snell's Law. This is still |
|
| 142:52 | . And all of these quantities here real. Everything you see here is |
|
| 142:56 | real number. But because the cosine one minus the square root of one |
|
| 143:06 | nine square root, this cosine uh now for post critical angles, this |
|
| 143:15 | is gonna be uh uh bigger than because of the minus sine, the |
|
| 143:20 | is gonna be imaginary. And what means is that the theta two is |
|
| 143:26 | . So sine theta two is who signed data two is imaginary data |
|
| 143:32 | itself is a complex number. And of this, for these post critical |
|
| 143:41 | , the reflectivity, exact reflectivity we back on page 38. That's a |
|
| 143:46 | number. OK. So what what does that mean? OK. |
|
| 143:55 | , oh look at this bad see this R here, that should |
|
| 144:01 | an arrow. Uh This is a f and, uh, uh, |
|
| 144:05 | had those and I corrected those. , uh, but I, I |
|
| 144:08 | I didn't correct this one and more them are gonna be coming up. |
|
| 144:13 | So, uh, uh, you make a note to yourself that, |
|
| 144:17 | , starting on page 98 we see arrows which have the wrong font and |
|
| 144:25 | looks like an R so that R be an arrow indicating a vector that's |
|
| 144:33 | on me. I've got to correct and I've gotta do it right |
|
| 144:37 | So, uh, it's gonna make problem for me for, uh, |
|
| 144:42 | , for reasons of my own which , uh you don't wanna know |
|
| 144:47 | but I'll, I'll try to get fixed by Friday and then I'll post |
|
| 144:55 | , a new, um, you file in the canvas. |
|
| 145:02 | So, uh, leaving that aside is our uh wave vector for the |
|
| 145:09 | wave. So it has a length omega over VT OK. And uh |
|
| 145:17 | the uh the two uh uh but a vector and how do we find |
|
| 145:26 | vector from the length? Well, just multiply by sine and by |
|
| 145:31 | And so the sine of the angle this a uh magnitude, this amplitude |
|
| 145:37 | the uh uh the X one component uh for this wave vector. And |
|
| 145:43 | gives the X three component. So see uh uh this one is real |
|
| 145:49 | uh uh now we, and this is imaginary. So uh just to |
|
| 145:56 | things uh well, uh I, think maybe it's useful or II I |
|
| 146:02 | in the next line the imaginary that thing is really imaginary. How do |
|
| 146:07 | , I do that? I simply uh uh multiplied this by eye. |
|
| 146:13 | so then uh uh that uh uh the sign inside the square root. |
|
| 146:21 | this is a real number inside the root because in this post critical cases |
|
| 146:26 | is bigger than one. So this is real. This is always |
|
| 146:32 | And the imaginary part is showing here . Now, the wave has this |
|
| 146:42 | uh uh uh exponential factor. And here, we have some uh uh |
|
| 146:46 | the, these should be arrows, ours. OK. So we have |
|
| 146:52 | vector dot X vector. And so , I uh putting uh uh uh |
|
| 146:58 | notation into here, uh we see the uh the wave is uh uh |
|
| 147:07 | huh has a, a variation with according to here and a variation with |
|
| 147:13 | according to here. So the X is oscillates because it's got an I |
|
| 147:19 | . This term does not oscillate. doesn't have any, I, what |
|
| 147:23 | to the I? Well, we have I times I equals minus |
|
| 147:28 | , there's the minus one. So the terms in this expression are real |
|
| 147:35 | it doesn't oscillate, it decays. this transmitted wave oscillates as it travels |
|
| 147:43 | the X direction. And it does uh and in the Z direction it |
|
| 147:48 | oscillate. So it's not an a wave going down at some angle. |
|
| 147:54 | , it's going exactly horizontal exactly parallel the interface and away from the |
|
| 148:03 | it has an exponential decay just like , just like uh we had for |
|
| 148:08 | waves. It's a decaying away from uh from the surface now because uh |
|
| 148:41 | the, the amplitude is given by complicated formula that we had before. |
|
| 148:47 | we can't use. Uh uh uh let's um uh I think at |
|
| 148:56 | point, let's think about the, exact expression for the a, the |
|
| 149:01 | , the transmitted P wave amplitude is uh equal to the incident amplitude times |
|
| 149:08 | transmission coefficient which is given here on 43. Um Right now we're on |
|
| 149:15 | 99. So this is page 43 back there. We showed you the |
|
| 149:21 | coefficient and it's got in there the data. And so uh this amplitude |
|
| 149:27 | complex, what does that mean? means that the transmitted wavelength is phase |
|
| 149:38 | from that of the infinite wave uh . And so what that means is |
|
| 149:48 | the uh the transmitted wavel is not look like the same shape as the |
|
| 149:54 | wavel. That was true, we , for smaller angles of incidence, |
|
| 150:02 | for most critical angles of incidence no true. And then, and we |
|
| 150:06 | say the same thing about the reflected critical reflected and post critical converted. |
|
| 150:15 | , as this wave travels horizontally along boundary at this uh apparent velocity, |
|
| 150:25 | transmitted wave forces the infinite medium above oscillate at the same apparent velocity. |
|
| 150:36 | . Uh Forces. So imagine now a post critical transmitted wave, it's |
|
| 150:44 | going down into the uh in into meeting, it's going along the boundary |
|
| 150:52 | it's decaying away from the boundary at depths. And as it goes along |
|
| 150:57 | boundary, it's wiggling the boundary and uh uh creating uh uh uh uh |
|
| 151:05 | another way of growing up. um So now, uh let's uh |
|
| 151:16 | let me back up that last Uh Stopping right here. Uh Oh |
|
| 151:23 | , we wiggle the incident medium as transmitted wave goes along horizontally, it |
|
| 151:29 | at the same parent velocity. So forces a plane wave to radiate upwards |
|
| 151:35 | the inst intermediate. Now, if incident wave is planar, such as |
|
| 151:41 | in the uh in most of the here we've talked about is planar um |
|
| 151:46 | infinite waves. Then this going uh wave is just the reflected B wave |
|
| 151:53 | we talked about before it propagates up this angle, reflecting angle equals this |
|
| 152:00 | . However, however, if the wave is curved, then this wave |
|
| 152:06 | is being caused by this um well critical reflection, that's a new way |
|
| 152:14 | operating up at the critical angle. there's gonna be more discussion about |
|
| 152:20 | Look. So hold that thought in mind. Now, before we get |
|
| 152:26 | there, I wanna point out to that it can also happen. Uh |
|
| 152:30 | you can imagine cases where the sheer in the lower medium is bigger than |
|
| 152:35 | P wave velocity in the upper Why not in the upper medium? |
|
| 152:42 | sheer velocity is always gonna be smaller the P velocity. But you can |
|
| 152:48 | where the lower medium has a sheer which is bigger than the P velocity |
|
| 152:54 | the upper medium. And in those , there's also a sheer critical angle |
|
| 153:02 | sheer critical angle is defined by you know, using Snell's Law. |
|
| 153:07 | so the sheer critical angle is the inverse side of this ratio here. |
|
| 153:12 | , you might think that's never gonna in exploration geophysics, but I'm here |
|
| 153:18 | tell you that it happens a lot a certain circumstance. And I'll tell |
|
| 153:27 | about that circumstance in the context of hall wave propagation later, I forgot |
|
| 153:35 | , how much later, but uh that's gonna come up where we have |
|
| 153:40 | sort of thing happening in the bore . And Schlumberger is measuring that all |
|
| 153:46 | day somewhere in the world. So me just show you a picture |
|
| 153:53 | uh, uh uh from uh Sheriff Geldart. And, uh this is |
|
| 153:58 | computed by them for uh a particular . And so uh uh you can |
|
| 154:04 | here that uh that uh this is reflection here. And so at, |
|
| 154:09 | uh uh uh at small angles, reflection is very slow, a very |
|
| 154:16 | and the transmission is very big. a matter of fact, this is |
|
| 154:19 | limiting case where at normal incident, um reflect the function coefficient is |
|
| 154:27 | transmission coefficient is a one. But larger angles, everything changes and then |
|
| 154:33 | here at the critical angles, everything complicated. And then further out |
|
| 154:38 | there isn't the sheer critical angle even . However, we do arrange most |
|
| 154:46 | our um our surface seismic, most our service seismic um surveys so that |
|
| 154:57 | have maximum offsets so that at the horizon, uh the the angles are |
|
| 155:05 | than the critical angle. So we have to worry about this kind of |
|
| 155:11 | uh uh for the target reflections in surface sizing data. If we looked |
|
| 155:21 | reflections from interfaces more shallow, we see these but it's, it's very |
|
| 155:28 | for us to ignore those uh those la large angle reflections at um shallow |
|
| 155:37 | from shallow horizons. How do we that? We do that by muting |
|
| 155:42 | , by setting to zero the traces for the uh at, at sh |
|
| 155:47 | short reflection times. So let me then turn to a quiz. So |
|
| 156:07 | think this one goes to uh uh . So you see Carlos uh we |
|
| 156:15 | down here all of the above. let's go down through these one at |
|
| 156:18 | time. And so I'm gonna ask Carlos only about uh a so it |
|
| 156:24 | for initative angles greater than the critical . Um Is it true that the |
|
| 156:32 | wave propagates parallel to the interface? that true? Hm. Uh So |
|
| 156:41 | what is I think for, for let me, let me rephrase |
|
| 156:45 | Is it true that the transmitted wave horizontally only or post for angles of |
|
| 156:54 | greater than critical? Is that I, I think it's not true |
|
| 156:58 | false. Yeah. Uh No, is true. We talked about |
|
| 157:03 | you know, for pre critical incidents for the small angle incidents, the |
|
| 157:10 | wave goes on down uh following the , logs at some angle, but |
|
| 157:14 | going down. But for uh for angles of instance, beyond critical as |
|
| 157:22 | just talked about, the transmitted wave not go down, it goes exactly |
|
| 157:28 | parallel to the interface. So this is true. However, look down |
|
| 157:35 | , we got all of the So maybe some of these others are |
|
| 157:40 | true. So before we select uh let's look at the next |
|
| 157:45 | So this one goes to mesa uh uh uh uh B is this true |
|
| 157:54 | infinite angles greater than the critical the transmitted wave decreases in amplitude away |
|
| 158:00 | the interface is that statement true. true. Yeah, it's true. |
|
| 158:05 | so now we have two of them . So we're expecting then that the |
|
| 158:09 | uh is gonna be all of the . But before we come to that |
|
| 158:13 | , I'm gonna uh look at enter uh And I'm gonna go to le |
|
| 158:19 | and say here for infinite angle greater the critical angle, does it have |
|
| 158:25 | shape different than the infinite wavelength? . Also true true. We got |
|
| 158:31 | of the above is true. Uh we're not done yet. Um We're |
|
| 158:39 | done yet. Uh So let's look E because if, if E is |
|
| 158:45 | , then we go to F, . So, uh so now, |
|
| 158:50 | in this case for, for infinite greater than the critical angle back, |
|
| 158:56 | to you Carlos for instant angle greater the critical angle. Is it true |
|
| 159:00 | the reflected wavelength has a shape different the infinite wavel? I think you |
|
| 159:07 | it was, it, it was true. I mean, it's, |
|
| 159:11 | OK. I know you said you that it's, that, that, |
|
| 159:16 | is the same. So that is . That would be so, so |
|
| 159:20 | our final answer is all of the . So, uh uh this is |
|
| 159:25 | tricky question. You got to think everyone. And so as soon as |
|
| 159:29 | got these two are correct, then expecting that it's gonna be d but |
|
| 159:34 | you uh answer D, you better at this one and uh uh the |
|
| 159:39 | answer is all of the above. . So next one, it goes |
|
| 159:44 | BEA and uh uh uh so true false. If the incident wave is |
|
| 159:50 | P wave, plain P wave, the most quickly reflected P wave propagates |
|
| 159:58 | at this angle, the, at critical angle uh not the incident |
|
| 160:05 | Uh uh Is that true or Let's go over it again. Uh |
|
| 160:14 | we have the infinite wave is a wave plane P wave. Then let's |
|
| 160:19 | at the uh uh reflected P wave angles larger than the critical angle that's |
|
| 160:26 | be probably getting upward. Now is is the angle gonna be a theta |
|
| 160:31 | or is it gonna be the same the incident angle? It's, it's |
|
| 160:39 | , it's false, it's false. . Now, I I'm gonna show |
|
| 160:44 | later another case where the reflected wave going up at this angle, not |
|
| 160:51 | this angle, but that's for curved , not for plan wavelengths. |
|
| 160:59 | So you are correct this one is . So, so that's the very |
|
| 161:03 | topic is waves, waves and curved . OK. So uh first let's |
|
| 161:12 | about uh curved wavelengths. So this normal, right? Uh whenever we |
|
| 161:19 | uh real data, it's always coming curved wavefront because it's always coming from |
|
| 161:25 | localized source and that wave radiates away the source, it's always curved. |
|
| 161:33 | so uh uh what does that Well, here it says that if |
|
| 161:37 | infinite wavefront is curved, talking about critical um uh reflections, then the |
|
| 161:47 | wave reflection coefficient has to be modified a term which is proportional to one |
|
| 161:53 | KRC. What, what is this is the length of the wave |
|
| 161:59 | And RC is the radius of curvature uh uh of the wave, |
|
| 162:05 | it's proceeding outwards from the source. it's curved and think of it as |
|
| 162:10 | uh um uh think, think of as AAA uniform over bird. So |
|
| 162:16 | wave as it goes out is a is a spherical wavefront, right? |
|
| 162:21 | we're looking at this in cross So we only see a circular wavefront |
|
| 162:28 | cross section going out from the source a uniform medium. And uh uh |
|
| 162:35 | the overburden is uniform, then this of curvature is the distance back to |
|
| 162:41 | source, that's the radius of that . And so in the, in |
|
| 162:45 | real world, of course, it's have layers and so on in the |
|
| 162:50 | uh but it'll, this radius of is still gonna be a, a |
|
| 162:54 | similar to um oh yeah. Uh the actual radius back to the |
|
| 163:04 | So let's uh manipulate this ratio The K is given by V over |
|
| 163:12 | . Omega is given by two if uh velocity over frequency is wavelength and |
|
| 163:22 | two pi is down here, it's equal to six. So this modification |
|
| 163:28 | is proportional to the wavelength divided by distance back to the reflector and a |
|
| 163:38 | . So what that means is after propagation distance of only one or two |
|
| 163:44 | , this correction is negligible and that's , uh uh gonna be true everywhere |
|
| 163:51 | near the critical angle. So that's we don't worry about wave like temperature |
|
| 164:00 | most of our data because for most our data, uh uh we have |
|
| 164:07 | uh uh maximal offsets so that we have critical angles in our data |
|
| 164:13 | And we have waves are, which propagated away from the source by far |
|
| 164:21 | so that the curvature can be And so that's why we get to |
|
| 164:27 | way. And that's what I I'm, I'm guessing that uh oh |
|
| 164:35 | guessing that in, in almost every discussion you heard about reflectivity, nobody |
|
| 164:42 | mentioned it. They only mentioned plane . And at that point, you |
|
| 164:47 | have asked your professor, you should said the professor, our waves are |
|
| 164:52 | plane waves, they curved wave. about the curvature? This is the |
|
| 164:56 | that the pine wave reflection coefficient, we already did is good enough. |
|
| 165:03 | soon as the radius of curvature gets be far enough away. And as |
|
| 165:07 | as the wavelength expands more than just or two wavelengths, because of this |
|
| 165:13 | here, the correction term gets to negligible for a large radius of curvature |
|
| 165:21 | propagation more than one or two wavelengths from in the short. Now, |
|
| 165:35 | let's draw that same uh uh let's draw uh the cartoons that we had |
|
| 165:43 | showing those curved rays. So uh first, let me look at uh |
|
| 165:50 | me point out to you here, have uh an interface uh but we |
|
| 165:55 | upper medium and the lower medium and lower medium is faster than the upper |
|
| 165:59 | . OK. So first look at dash lines, straight dash lines, |
|
| 166:04 | are wave vectors incoming uh uh reflected transmitted. But now for the first |
|
| 166:11 | , I'm also gonna draw some curved . So here is the curved, |
|
| 166:17 | infinite wavefront. You see it's got radius of curvature. If the overburden |
|
| 166:23 | uh uh uh his uniform, then can see that this comes from a |
|
| 166:30 | somewhere up here making us uh this a fraction of a circle from a |
|
| 166:36 | somewhere up here. I'm just showing this part. OK. Now, |
|
| 166:41 | look at the reflected curvature here is the reflected wavefront. So it's also |
|
| 166:48 | and it comes from what we call image of a AAA mirror point a |
|
| 166:55 | source. So as you can see this one here looks like it comes |
|
| 167:01 | AAA from a circular source down here which is in the mirror image of |
|
| 167:08 | source. Here. If we imagine interface to be a mirror, then |
|
| 167:14 | we have a source point up we have a, a mirror image |
|
| 167:18 | that point somewhere down here. And making this uh reflected curvature here. |
|
| 167:26 | , the refracted cur the refracted refracted wave, a wave looks like |
|
| 167:33 | Here is our we transmitted refracted wave and uh uh see uh theta two |
|
| 167:42 | bigger than theta zero. So so the transmitted angle is bigger than |
|
| 167:50 | infinite angle that happens because of Snell's . And because the uh velocity down |
|
| 167:57 | is larger than the velocity up So the wave is refracted closer to |
|
| 168:03 | horizontal away from the vertical, closer the horizontal because this is faster down |
|
| 168:09 | . And so it's making a wavefront is uh looks more like this. |
|
| 168:14 | has AAA radius of curvature. Uh mean the, the, the, |
|
| 168:20 | apparent center of this circle is somewhere here. OK. Now, I |
|
| 168:30 | say that the appearance of these wave complicates this cartoon a lot. That's |
|
| 168:36 | we didn't draw them before we only the wave vectors for plane waves. |
|
| 168:41 | Now, for third rays, we these bird wavefront instant reflected and |
|
| 168:49 | Yeah, this intersection point travels to uh to the right following this apparent |
|
| 169:05 | velocity. Uh this apparent velocity uh uh a V one overs sign data |
|
| 169:12 | it's also equal to V two over data two according to St's law. |
|
| 169:18 | uh uh so wherever a a as wave uh uh uh progresses, see |
|
| 169:31 | wavefront a and after a few uh milliseconds, this wavefront is gonna be |
|
| 169:37 | here curving up like so, and uh these other waves are gonna follow |
|
| 169:43 | . The whole thing moves together sideways this apparent velocity. And where does |
|
| 169:51 | sine data come from? Well, saw that before, when we were |
|
| 169:54 | at at P waves, uh go and check that to see why the |
|
| 170:00 | data appears down here. And remember data is a number less than |
|
| 170:05 | So this apparent velocity is faster than V one velocity. Now, all |
|
| 170:13 | this uh uh I haven't shown uh uh I haven't said here whether this |
|
| 170:23 | is uh uh uh less than the angle or more than the critical |
|
| 170:29 | Now, in the next slide, gonna say it's more than the critical |
|
| 170:33 | . So, uh uh uh in that case, the uh uh |
|
| 170:40 | incident wavefront looks like this and you the source is way over here. |
|
| 170:45 | here is the uh the incident uh theta zero is the angle all the |
|
| 170:54 | from here to here. I think should have know maybe drawn this |
|
| 171:00 | But this angle, the theta measures distance from the vertical all the way |
|
| 171:05 | here to the incident wave vector. not this part here. It's all |
|
| 171:11 | way over to the infinite wave vector ear to ear. And so the |
|
| 171:16 | wavefront curved wavefront looks like like And the reflected cur boy looks like |
|
| 171:23 | because that's coming from some uh uh that that's looks like it's coming from |
|
| 171:31 | , a mirror source point down here . It's the mirror image of the |
|
| 171:37 | point up here, which is um the real source point and the refracted |
|
| 171:44 | is coming along this way at the uh at this uh at the apparent |
|
| 171:56 | . Well, you see this additional here connecting this point to the tangent |
|
| 172:19 | the reflected line here. That straight here means that in this circumstance where |
|
| 172:30 | most critical incident with curved wavefront, is an additional term uh uh uh |
|
| 172:40 | in the solution, which means uh which leads a ha ha has a |
|
| 172:47 | wavefront going up from the um And what is the orientation of |
|
| 172:56 | Well, this is the uh the angle and it's uh and uh thi |
|
| 173:03 | is called a head wave he head hea D and you see it, |
|
| 173:10 | um um straight line here. Uh , if you're thinking in terms of |
|
| 173:28 | uh this to be a cross section a real uh uh uh 23 dimensional |
|
| 173:35 | . This is um uh this looks um AAA cross section of a shear |
|
| 173:44 | . And this is the cross section a cone. So I like an |
|
| 173:49 | cream cone. And so uh uh has uh here's the point of the |
|
| 173:56 | and here is the straight side of cone. So we show this as |
|
| 174:01 | because uh uh uh right, the there are decreasing away from the uh |
|
| 174:15 | the interface. So right here, , I'm proving to you that, |
|
| 174:20 | this angle, the head wave angle equal to the critical angle. Why |
|
| 174:26 | why you can work out for yourself uh uh the distances here. And |
|
| 174:31 | uh this distance is uh three two times delta T uh uh uh |
|
| 174:38 | what is delta T, delta T the time it takes from uh uh |
|
| 174:43 | prediction here to here. And uh this is propagating at the uh uh |
|
| 174:50 | velocity, this is propagating at the velocity. So uh uh this is |
|
| 174:58 | so it turns out that then the wave is propagated at the same angle |
|
| 175:04 | the critical angle for this post critical . So the critical uh uh this |
|
| 175:12 | angle theta zero is coming in at angle bigger than the critical angle. |
|
| 175:17 | don't see the critical angle in but you do see the head wave |
|
| 175:20 | which is turns out to be numerically to the critical. Now, this |
|
| 175:26 | wavefront is a linear even though the wave is curved. If we were |
|
| 175:35 | here in 3d, there would be conical wavefront and there might be other |
|
| 175:42 | waves associated with other outgoing waves or to other critical angles, for |
|
| 175:49 | the shear wave critical angles. So me show you then uh a diagram |
|
| 175:55 | really gets amazingly complicated. And this is calculated uh that may be better |
|
| 176:02 | uh uh uh the cartoons that I showed this diagram comes from sheriff and |
|
| 176:08 | are. So uh all these are arrival times of various modes coming from |
|
| 176:16 | source point here. So at normal , you ha uh have um uh |
|
| 176:24 | wave reflection. And uh and uh here, look here, here's a |
|
| 176:29 | the P wave uh reflection arrival and uh the, the figure is cut |
|
| 176:36 | but you can, you know, can um uh extend this in your |
|
| 176:41 | down here. And so down somewhere way down here uh is |
|
| 176:46 | a reflected wave arrival. And here , if the, if the source |
|
| 176:52 | also sheer waves in it, we have an uh uh uh a direct |
|
| 176:57 | uh sheer wave. And um uh uh let's see here, I'm saying |
|
| 177:08 | wrong. Uh uh So I'm so let me ST uh I'm getting |
|
| 177:16 | of myself. So let's step through diagram one piece at a time. |
|
| 177:21 | got our source here and the infinite wave is given here. So you |
|
| 177:28 | this is a fraction of a curve that there are uh a circle and |
|
| 177:34 | uh center of that circle is back at the uh uh at the source |
|
| 177:40 | . OK. Now, what's Well, you can see a reflected |
|
| 177:45 | wave. So the reflected P wave also a circle like so and it |
|
| 177:51 | to be coming from a mirror point which is uh directly be beneath the |
|
| 177:58 | here. So that's the reflected wave here. OK. Next, we |
|
| 178:05 | a refracted P wave that's coming from . That's the one that I was |
|
| 178:10 | and trying to describe that's a AAA refracted P wave. Uh But uh |
|
| 178:20 | amplitude, this does not show you amplitude, we know already that these |
|
| 178:26 | are decreasing away from uh uh away the interface. So next point is |
|
| 178:37 | head wave that I just showed So this head wave connects this um |
|
| 178:44 | here with this point here. So , it's tangent to the reflected P |
|
| 178:49 | just like I showed you before. it's inter syncing the interface at um |
|
| 178:55 | position which is provided by uh the yeah transmitted critically refracted he wave in |
|
| 179:12 | uh uh in the sub surface. this is traveling with uh uh with |
|
| 179:17 | velocity of VP two in the sun . And uh so this uh linear |
|
| 179:26 | wave is uh that's the critical angle here. OK. So next, |
|
| 179:34 | showing uh uh let's see, um up, one, back up |
|
| 179:42 | OK. So, going forward so here is the reflected wave. |
|
| 179:48 | uh so uh you only get a wave, of course, it uh |
|
| 179:53 | normal incidents when you have a which uh is a uh a sheer |
|
| 179:58 | . So the this is for uh incident, she reflected sheer and that |
|
| 180:05 | you this um uh circle right And oops we get another head wave |
|
| 180:20 | from this point back to this circle uh that's we call that head wave |
|
| 180:28 | . What happened? Oh Here's head two and three. And here see |
|
| 180:33 | , they're connecting uh uh uh all points together with cha becoming tangent to |
|
| 180:41 | curve wavefront. Back here, there's the refracted sheer wave down here. |
|
| 180:48 | the critical, the sheer critical angle shown uh in here. So you |
|
| 180:53 | see how very messy this can be here's head wave six, not that |
|
| 181:00 | . So uh so very messy arrivals critical in the case where um uh |
|
| 181:11 | the lower medium is faster than the medium. So now when does that |
|
| 181:18 | whenever the incident angles are large? also you need to have a strong |
|
| 181:23 | increase. So as the examples, if you're doing surface seismic um surface |
|
| 181:34 | surveys, if you have an interface , with this uh sediment above and |
|
| 181:39 | below, that is gonna make a of this kind of phenomenon. How |
|
| 181:45 | um uh plastic sediment above and carbonates ? Also, you see it there |
|
| 181:52 | the carbonates are fast, the salt fast, the salt is fast. |
|
| 181:56 | if, if you have the salt sediments, you're gonna see these kinds |
|
| 182:02 | um of events. If you look them now, it seems all pretty |
|
| 182:09 | . And I would say that because esoteric, mostly we arrange our data |
|
| 182:17 | that these arrivals don't show up. , and, and I think that's |
|
| 182:25 | good idea. However, here's another idea. Maybe we should arrange our |
|
| 182:32 | so that they show up strongly. we would learn something about the |
|
| 182:38 | If we looked at these post critical reflections, I can, I can |
|
| 182:45 | you that none of your colleagues knows about post critical reflection and you don't |
|
| 182:50 | much either, you know, you already know more than your colleagues |
|
| 182:54 | . Um But uh maybe if we um wanted to, we would find |
|
| 183:04 | something valuable by observing these post critical . So I'm gonna leave you with |
|
| 183:09 | thought for surface seismic that maybe instead ignoring these things, maybe we should |
|
| 183:16 | looking for them and have them. we will learn something important I don't |
|
| 183:21 | the answer to that question, but , it's a sort of question that |
|
| 183:25 | might ask yourself. Uh Would it useful for us to uh do something |
|
| 183:32 | ? Then all of our colleagues are these things, maybe uh we're throwing |
|
| 183:38 | the uh uh important information there. there is a ca uh there is |
|
| 183:45 | contact in exploration of geophysics where these are common and that is in Sonic |
|
| 183:55 | . OK. So, uh so let's turn our attention away from surface |
|
| 184:02 | and think about the context of Sonic . So here's a cartoon uh uh |
|
| 184:12 | Lock and we have uh a cross here, river cross section here. |
|
| 184:15 | can see the formation here, you see our borehole here. You can |
|
| 184:21 | that the source in this case, is uh is a source which sends |
|
| 184:28 | P waves through the mud that is here. So this sends out P |
|
| 184:34 | through the mud in all directions, and down all it's, it's called |
|
| 184:38 | monopole source. So it uh it out uh P waves in all |
|
| 184:46 | doesn't send out any sheer waves that the mud doesn't allow any sheer waves |
|
| 184:52 | propagate. So let's look at this wave right? This P wave right |
|
| 184:57 | , it goes out and it hits , the uh formation wall at an |
|
| 185:02 | not 90 degrees and it refracts this because the formation has a P wave |
|
| 185:11 | faster than the P wave velocity in mud. So the wave following snow |
|
| 185:18 | , the w uh the wave is towards the axis of the moral. |
|
| 185:26 | this surface here is a cylindrical not a flat surface, but uh |
|
| 185:31 | uh Snell's law still applies in modified . And so this wave goes off |
|
| 185:37 | the formation never comes back, we see that one again, but there |
|
| 185:43 | other angles. So right here here AAA wave through the uh mud where |
|
| 185:52 | , the it it's the formation wall an angle which is large enough so |
|
| 185:58 | it's making a critically refracted p wave exactly along the borehole wall. |
|
| 186:07 | I I here, it's here, refracted towards the borehole axis. |
|
| 186:13 | it's refracted exactly along the borehole axis it goes along the borehole axis, |
|
| 186:19 | ripples, it makes a little ripple the uh wall here and that sends |
|
| 186:25 | back the waves back through the mud the same critical angle. This angle |
|
| 186:31 | that you see here is the same this angle here. That wave goes |
|
| 186:35 | the way up. Now, we've got a receiver sitting here and |
|
| 186:42 | this wave critically refracted back into the uh borehole mud. It's this |
|
| 186:50 | how did it know that this receiver gonna be here? So that in |
|
| 186:55 | uh uh uh do this refraction? , the answer is that as it's |
|
| 187:01 | along here, it's sending energy back the medium at the critical angle everywhere |
|
| 187:07 | goes, this is the one which received by this receiver because um uh |
|
| 187:15 | going back into the media at the ending, that's the head wave that |
|
| 187:20 | talked about before. And um uh uh the arrival time from here from |
|
| 187:29 | to here depends upon the D wave body p wave velocity uh in this |
|
| 187:37 | from year to year. So, and uh of course, uh uh |
|
| 187:43 | the logging company knows what this distance . It measures the arrival time. |
|
| 187:49 | it gets the average velocity between here here. But uh a modern company |
|
| 187:55 | when Schlumberger invented this um back in , they invented this basic idea back |
|
| 188:06 | the uh 19 thirties, I think the 1940. And at that |
|
| 188:11 | they had only one receiver here. , since then, logging companies have |
|
| 188:16 | much more clever. And so now modern login tool has not only one |
|
| 188:21 | here, but maybe a dozen, only showing two with me, maybe |
|
| 188:25 | a dozen uh uh receivers here. you can see that the uh the |
|
| 188:33 | in arrival time between this receiver and one comes from the average velocity in |
|
| 188:38 | . So that's much higher resolution, it than we have here. |
|
| 188:43 | uh uh uh that gives uh so the average sonic velocity in this |
|
| 188:48 | . And so companies like Schlumberger uh really expert in handling this kind of |
|
| 188:58 | . And if they have a 12 here instead of uh two, then |
|
| 189:02 | gonna have linear move out, not move up, linear move out as |
|
| 189:06 | wave goes up ball. OK. that's the way we do P wave |
|
| 189:15 | . And there's uh there's lots of enhancement. But that's the, the |
|
| 189:20 | idea using the concepts that we just are critically refracted waves P waves. |
|
| 189:32 | , next picture is gonna be showing next picture is be gonna be showing |
|
| 189:39 | um uh uh shear waves. So why not do shear waves? |
|
| 189:45 | look here uh uh here, we uh uh uh another arrival from the |
|
| 189:54 | source. And can you see this is a bigger angle than this angle |
|
| 189:59 | here? But this is the angle uh uh for a critical angle for |
|
| 190:06 | conversion from P to S. So um uh uh transmitted wave is, |
|
| 190:14 | going up along the borehole at the wave velocity of the uh uh of |
|
| 190:22 | sheer wave. And as it it's putting energy back into the um |
|
| 190:28 | borehole at the critical angle. Can see this angle is different from this |
|
| 190:39 | ? And in the same way, uh similar way as we had here |
|
| 190:44 | the P waves. Uh The, first arrival here gives the average velocity |
|
| 190:49 | this point and this point of the . And then the difference in uh |
|
| 190:55 | arrival time between here and here. gives the average velocity in this little |
|
| 191:00 | here. And you can see that you have 12 receivers, you can |
|
| 191:06 | some clever um data processing workflows to out the um uh uh the sheer |
|
| 191:20 | . Even though the same receivers are the, the P waves, you |
|
| 191:24 | , the P waves are, are are are traveling faster than the sheer |
|
| 191:29 | . And so uh the, the opera logging companies know how to |
|
| 191:34 | this and they separate out the uh sheer wave velocity like that. So |
|
| 191:44 | looks like it's uh uh uh uh , the end of that discussion. |
|
| 191:49 | wait, there's more what happens if have what's called slow sheer formation. |
|
| 192:01 | a case like this, the sheer in the formation is less than the |
|
| 192:11 | wave velocity in the mud. of course, the slow, |
|
| 192:15 | of course, the shear wave velocity the formation is less than the B |
|
| 192:21 | velocity in the formation. But um talking about uh uh segments which are |
|
| 192:28 | slower so that the sheer wave velocity is less than the P wave velocity |
|
| 192:33 | the mud. So, uh so , the mud uh uh velocity is |
|
| 192:40 | around 1500 m per second. And the shear wave velocity in the formation |
|
| 192:47 | lower than that. In that the waves are gonna be refracted away |
|
| 192:54 | the borehole wall following snail's walk So don't have this situation where the sheer |
|
| 193:01 | are retracted towards the, the borehole . And this, this is a |
|
| 193:08 | refraction here that happens when the sheer velocity here is faster than the P |
|
| 193:14 | velocity in the mud. So in s uh slow sherm information, and |
|
| 193:19 | have a lot of these a AAA of the sediments that we explore |
|
| 193:24 | in the Gulf of Mexico and, shallow uh environments everywhere has this uh |
|
| 193:30 | that the sheer velocity in the formation less than the P velocity in the |
|
| 193:37 | . So the previous algorithm doesn't All the body waves get refracted away |
|
| 193:42 | the borehole axis and never come And so they don't receive anything up |
|
| 193:48 | . So that was a bummer and so uh uh this problem was |
|
| 193:53 | about, I would say 30 years . And here I think maybe slim |
|
| 193:57 | was uh I was responsible for this . They developed something called a dipole |
|
| 194:08 | . So the dipole source is not this monopole source. The dip source |
|
| 194:14 | out a P wave with a positive , positive polarity this way and a |
|
| 194:20 | polarity this way. In other it kind of sucks the, the |
|
| 194:25 | in here and pushes it out Whereas this one pushes the fluid out |
|
| 194:29 | all directions. That's a simple. they have dipole sources here which, |
|
| 194:35 | give a positive pulse in this And a negative pulse in this direction |
|
| 194:40 | it hits the borehole um sideways like shows and that portal wave travels up |
|
| 194:51 | borehole wall like so, and it's received up here with dipole receivers. |
|
| 194:57 | when this torsional wave gets up that's detected with dipole receivers, and |
|
| 195:02 | may be a dozen of them going here. And uh uh this way |
|
| 195:07 | travels up but it vibrated sideways because the, the source here. So |
|
| 195:17 | uh this to wave travels with a which is not equal to the body |
|
| 195:24 | uh velocity and the uh of the waves, it's like a surface wave |
|
| 195:30 | it travels with a velocity which depends the body wave velocity for sheer waves |
|
| 195:40 | the body of the formation. And requires a correction for uh uh a |
|
| 195:45 | dependent correction to uh uh determine the what we really want to know is |
|
| 195:52 | body wave velocity here, not the personal wave velocity. So companies like |
|
| 195:58 | and Baker Hughes and uh so they know how to do this. |
|
| 196:01 | so that is what comes from um dipole source and this was invented like |
|
| 196:09 | years ago. Now, this is the tool that was invented by Schlumberger |
|
| 196:16 | Amico simultaneously. Back in 1986 in there, they invented what we call |
|
| 196:24 | cross dipole tool. So that's uh from this. And I will delay |
|
| 196:33 | discussion of the cross dipole tool until in the course. So, |
|
| 196:52 | let's consider it. Now, the where we have plane waves incident upon |
|
| 196:58 | curved reflector. So that's gonna be a very similar analysis except that we |
|
| 197:04 | not gonna be able to uh necessarily assume that the radius of curvature |
|
| 197:10 | large. Uh And depending, uh this is gonna have a curve |
|
| 197:15 | So maybe, uh uh you uh maybe the sedimentary layers were laid |
|
| 197:21 | flat uh years ago, millions of ago. And then maybe uh tectonics |
|
| 197:29 | , maybe they would deform tectonically uh the interim. And now, maybe |
|
| 197:35 | uh the reflector is curved, you easily imagine that that that might |
|
| 197:42 | So, uh uh also the reflector has two different radii of curvature, |
|
| 197:50 | know, like a saddle has Yeah. And if you're sitting on |
|
| 197:56 | saddle, that saddle is curved both to side where your legs are going |
|
| 198:02 | the side and it's also curved front back. Uh uh uh so that |
|
| 198:07 | holds your butt in place on the . And maybe those two curvatures are |
|
| 198:13 | in the two different directions. So could be true also with a curved |
|
| 198:18 | reflectors in the subsurface, you because of the complexity of tectonic |
|
| 198:24 | why not? So these curve reflectors to focusing and def focussing via the |
|
| 198:33 | of waves as we are gonna discuss further in uh lesson seven, So |
|
| 198:41 | now, we're only gonna uh uh it at that and um uh almost |
|
| 198:47 | let's have a couple of quiz questions about curved wavefront is this statement true |
|
| 198:54 | false? And I think this one to versa. We don't, it |
|
| 198:58 | we don't care if the instant wave curved or not. Since an explanation |
|
| 199:03 | is explained waves are an acceptable Is that true or false? And |
|
| 199:10 | so what do you think per I don't know if this one |
|
| 199:17 | Yeah. Yeah. So uh that's bit of it. And yeah, |
|
| 199:22 | I'm gonna say that that this statement false because there are many cases where |
|
| 199:27 | waves uh uh uh are not an uh uh uh a approximation. But |
|
| 199:39 | let me see here uh from uh I, I'm gonna say that this |
|
| 199:44 | is false because uh we just showed cases where plane waves are not an |
|
| 199:50 | approximation. And let's see here. , I'm having a problem here. |
|
| 200:07 | . Mhm OK. Sure. I I solved my problem. OK. |
|
| 200:17 | Oops. OK. So this is , this is the one we just |
|
| 200:24 | answered. So uh uh the next is for uh uh le le and |
|
| 200:32 | says even if the wave wavefront is , the plane wave approximation is usually |
|
| 200:40 | accurate as long as you have propagated from the source, a couple of |
|
| 200:46 | . Is this true or false? you know, I uh we |
|
| 200:52 | I think you said your, your is very softly le uh uh I |
|
| 200:57 | it's true. We, we always uh uh we always use the plain |
|
| 201:04 | of approximation, almost always, even the wavelengths are curved. And why |
|
| 201:10 | we get away with that? It's if you go uh just a couple |
|
| 201:14 | wavelengths away from the source, that's an accurate approximation. We talked about |
|
| 201:19 | . So uh that one is The only cases where we need to |
|
| 201:28 | the curvature of the wavefront is uh the critical angle and beyond. |
|
| 201:37 | This one goes to you Carlos uh or false for shallow reflecting interfaces, |
|
| 201:44 | maximum offset might allow for maximum incident which are beyond critical so that these |
|
| 201:52 | critical headways are recorded even though they're recorded at the target horizon deeper. |
|
| 201:58 | that one true or false? Mhm want to hear you thinking out |
|
| 202:06 | Carlo. Yeah, I know I still reading, trying to understand the |
|
| 202:12 | . Mm Yeah. So read it yourself out loud. Mm II I |
|
| 202:21 | it's true professor. Yeah, I it's true also. Now maybe that's |
|
| 202:27 | a good advice. Uh uh um me. Uh uh uh that I |
|
| 202:34 | it's probably true that we have in data as we record them, these |
|
| 202:41 | critical phenomena, but we don't look them. Uh maybe we should uh |
|
| 202:48 | uh the the statement as written, gonna say is true. And um |
|
| 202:55 | question goes to Mesa. So you here at the bottom we got all |
|
| 203:00 | the above. So uh let's think these one at a time. So |
|
| 203:03 | first one goes for Merce says these critical reflections, they come from an |
|
| 203:10 | with a faster formation below the interface uh uh do they a contain reflected |
|
| 203:17 | waves which are not present in uh rec critical reflections? That is |
|
| 203:26 | Yeah, that is true. Uh The statement is correct, but |
|
| 203:31 | the others are correct also. So me go to Lee Lee, how |
|
| 203:36 | um waveform? The, the, , those critical reflections have waveforms which |
|
| 203:42 | phase shifted from the infinite wave? , that's also true. But uh |
|
| 203:47 | we have two little truths. So we're suspecting D but before we get |
|
| 203:52 | D, we're gonna uh go to sea. And um uh uh Carlos |
|
| 204:00 | the, these um reflections have amplitudes are decreased by the geometrical spreading associated |
|
| 204:09 | the longer path lengths. Um Is true? Yeah, of course, |
|
| 204:14 | true. Whenever you have a longer length, you have more geometric |
|
| 204:18 | So those it's gonna affect the So uh uh we got all of |
|
| 204:22 | above. Very good. And uh so now to you, Brisa, |
|
| 204:29 | that's good. This one comes to , do these post critical reflections occur |
|
| 204:34 | not in a Sonic loin context. what, yeah, that's what they |
|
| 204:40 | occur in the Sonic logging context. uh if it were not for |
|
| 204:45 | then a big fraction of slumber say hole business would not exist. They |
|
| 204:50 | only be doing like red measures. uh uh there's lots of uh uh |
|
| 204:57 | Sonics being done these days and uh slumber gets their share of that, |
|
| 205:03 | business and makes a lot of money that. So uh what we have |
|
| 205:09 | is a summary slide. And so there is a list of all the |
|
| 205:16 | we've done. Uh We skipped over introduction, you read that on your |
|
| 205:20 | . But we talked in depth about Elasticity Hooks Law and all of that |
|
| 205:25 | stiffness tensors, compliance tensors. all of that, we talked about |
|
| 205:30 | uh put that in the way. uh When we consider how a wave |
|
| 205:36 | through a body uh using elasticity, We found out what the wave equation |
|
| 205:42 | like a uh and with various scalar wave equation vector wave equation, |
|
| 205:48 | cetera. And we even looked at anisotropic wave equation. We looked at |
|
| 205:54 | equation where, where the source then uh we said, OK, let's |
|
| 206:00 | at solutions. So we have body solutions and surface wa uh solutions. |
|
| 206:07 | the most important arrivals that we're most in in our surface sizing data are |
|
| 206:13 | reflections. So we spent the last hours talking about those. Now, |
|
| 206:18 | com completes our study of the most topics of waves and ray. |
|
| 206:28 | there's more. And so, uh, the next lecture is gonna |
|
| 206:35 | about complications, keeping the basic assumptions we had here, there's lots of |
|
| 206:45 | . And so we're gonna spend Friday about these and then Saturday, we're |
|
| 206:51 | talk about, uh, uh, gonna admit that one of the basic |
|
| 206:56 | we made right here at the right here at the beginning, we |
|
| 206:59 | we turn to Mr Hook and we Hook's Law starting from the beginning. |
|
| 207:05 | Hook's law only applied to um homogeneous media like copper or blast. |
|
| 207:14 | we've been applying ideas from elasticity to , but rocks are obviously in |
|
| 207:23 | they have grains and they have pores the grains. There's some minerals and |
|
| 207:28 | there's other, other minerals. And we should not be applying books law |
|
| 207:35 | such materials. We do it Why is that? Because not so |
|
| 207:42 | ago, starting in 1941. So my lifetime. I was born in |
|
| 207:49 | . So just before I was uh uh we uh learn how to |
|
| 208:01 | apply to modify Hook's Law for cases , of heterogeneous rocks. And we |
|
| 208:12 | out that uh uh on the one , the presence of the poorest make |
|
| 208:18 | of complications. And on the other , if you think about it, |
|
| 208:24 | , the complications are not so So in that case where we consider |
|
| 208:31 | uh when we have uh look at special cases, which are basically low |
|
| 208:38 | at low frequency, then we're gonna out that po elasticity looks a lot |
|
| 208:45 | elasticity and we can apply most of we learned. So that's good |
|
| 208:50 | We did not waste our time all . Uh Here, it's, I |
|
| 208:55 | you're thinking, wow, that's good . I thought I wasted all my |
|
| 208:59 | here but we did not. We learn on uh uh next Saturday, |
|
| 209:06 | will learn about uh uh how to the theory of elasticity to include both |
|
| 209:14 | and pores. And it's gonna turn better than you might have thought, |
|
| 209:19 | also has a lo a lot of interesting uh aspects to it. And |
|
| 209:25 | Saturday afternoon, we're gonna find out rocks are not perfectly elastic. They're |
|
| 209:33 | perfectly poor elastic either, but they attenuation in and it, and the |
|
| 209:39 | is gonna be responsible for effects that see in your data every day. |
|
| 209:45 | , if you leave this lecture and at your workstation, you will see |
|
| 209:50 | at long reflection times the frequencies are are smaller than to make lo lower |
|
| 209:58 | than at short reflection times. What means is that the high reflection, |
|
| 210:03 | frequency reflections got lost uh at long time, they got a absorbed, |
|
| 210:10 | got attenuated. That doesn't happen according hook, but it does happen in |
|
| 210:16 | Real World. So we're gonna have learn about that here. So that |
|
| 210:20 | gonna consume these three lectures are gonna our next week together. And then |
|
| 210:28 | following week we meet only on the and starting on Saturday. You have |
|
| 210:33 | new course. I, I don't what it is. I think it's |
|
| 210:37 | Zhou, that Professor Joe is gonna talking to you next Saturday on |
|
| 210:44 | I'm gonna be talking, say it . 00, all right. |
|
| 210:52 | so we're gonna, uh, be a delay, delay of a |
|
| 211:06 | . Oh, ok. So following last lecture in anisotropy, I'm gonna |
|
| 211:13 | handing out to you, uh, final exam and like I said, |
|
| 211:19 | would be, uh, an exam is gonna be, uh, |
|
| 211:23 | uh, unlimited time. You'll be to spend as much time as you |
|
| 211:28 | . A and so, um, you got, you gotta spend all |
|
| 211:33 | time in one city. So I'll out the exam on Friday and I |
|
| 211:39 | it will be due the next Not sure about that. I, |
|
| 211:44 | tell you exactly, but I think be due the following Wednesday. So |
|
| 211:50 | means you have several days to study you can't look at it during those |
|
| 211:55 | . You have to, uh, it closed up. But then when |
|
| 211:59 | finally decide to take the course, gonna do that at a time when |
|
| 212:04 | have lots of time. So if have family responsibilities. You choose a |
|
| 212:10 | when, uh, uh, your responsibilities are not gonna interfere and you |
|
| 212:15 | several hours to concentrate on this Now, I'm gonna design the exam |
|
| 212:22 | that I think you can do it three hours. But you don't have |
|
| 212:28 | restrict yourself to three hours. You have 30 hours if you want. |
|
| 212:32 | know, but you're gonna do it in one city. When you're doing |
|
| 212:38 | exam, you can have these lectures front of you in hard copy or |
|
| 212:44 | your computer or what is what we . It's an open book, unlimited |
|
| 212:49 | exam. Furthermore, not only these are, are in front of you |
|
| 212:55 | any book that you want, you have open in front of you while |
|
| 212:58 | taking the exam and you'll have plenty time to read those uh lectures during |
|
| 213:05 | exam because unlimited time. So there's con you won't, you're not allowed |
|
| 213:13 | have any consultation with other people. consult with each other. You can't |
|
| 213:19 | with your friends, uh your Nobody. This is your work |
|
| 213:24 | And of course it's gonna be on honor system. We trust you to |
|
| 213:28 | these rules. Exactly. So you're be sitting there uh in a quiet |
|
| 213:35 | with all your books. Lots of available and you're gonna do the |
|
| 213:40 | Uh I suspect that it might take more than three hours. I'm gonna |
|
| 213:44 | to limit it to three hours. I can tell you this, I |
|
| 213:48 | fail. Students. Always take more three hours. It's because they're nervous |
|
| 213:53 | they wanna do the best job they . Right. You go through the |
|
| 213:57 | and answer everything perfectly. You're still happy. You go back and check |
|
| 214:02 | . It might be more than three . So give yourself a time when |
|
| 214:06 | have more than three hours. Then you're gonna do is you're gonna send |
|
| 214:10 | results. You can do that any between the time I hand them out |
|
| 214:16 | the time they're due it'll be about days. But when you're done, |
|
| 214:22 | you're done, you, uh, , close the exam, you mail |
|
| 214:26 | off to Utah, not to but to, you mail it to |
|
| 214:31 | to and then he will collect them and when he's collected them all, |
|
| 214:35 | send them to me. So then take me a while to grade them |
|
| 214:40 | too long because we have only three you here. But, um, |
|
| 214:46 | , uh, I will grade uh, in, in the next |
|
| 214:49 | days and then send, uh, them back to you. So, |
|
| 214:57 | , that's the, uh, that's way it's gonna work and all of |
|
| 215:01 | is gonna be triggered by, you, you're gonna receive the, |
|
| 215:07 | , the exams in hard copy following last lecture, following the convenient and |
|
| 215:17 | it to you in your hand. , uh, let's see how are |
|
| 215:20 | gonna get it to? This is be a problem here. Um, |
|
| 215:28 | am I gonna get it to, , our, uh, to, |
|
| 215:31 | , Carlos and to Brisa can't give by hand. Uh, so, |
|
| 215:38 | , uh, first, let me to your Brisa. Are you ever |
|
| 215:41 | campus so that we can give it you in your hand? Uh, |
|
| 215:46 | , I could go if needed. , so you, you could drive |
|
| 215:53 | , uh, you, you are now in Slumber in Sugarland. Am |
|
| 215:56 | correct? No, in West Chase , on Richmond Avenue. In, |
|
| 216:01 | , in Richmond. Oh. so not so far. Uh, uh |
|
| 216:06 | , that, uh, when you Richmond earlier, I thought the town |
|
| 216:09 | Richmond, you mean on Avenue? . So I know where that |
|
| 216:14 | It's, it's at, uh uh uh uh it, it's at Richmond |
|
| 216:21 | uh uh uh yeah, and uh, Briar Forest. Yeah, |
|
| 216:25 | used to live right, right nearby . Ok. So you could drive |
|
| 216:31 | but Carlos cannot. So how would go about getting the exam? |
|
| 216:39 | I can do email but see, a problem because when he receives the |
|
| 216:44 | , he looks at the exam, think we'll do it this way for |
|
| 216:48 | Meader and uh uh and for um uh uh book for both me and |
|
| 216:56 | Carlos and why not for Lee we'll do it all by email. |
|
| 217:02 | all three have the same choice And when you get this email, it's |
|
| 217:07 | say in the email, it says gonna say final exam do not open |
|
| 217:12 | until you're ready to take it. , so you can do that. |
|
| 217:17 | so here's what I'm gonna suggest, gonna suggest that the first thing you |
|
| 217:21 | when you open it is to print off, just you, everybody has |
|
| 217:26 | local printer so you can print And then I think it's gonna be |
|
| 217:32 | for you to answer your questions if have hard copy. So, so |
|
| 217:36 | can do, you can do your you with your pen and, |
|
| 217:41 | and pencil on the hard copy. the first thing you do when you |
|
| 217:45 | it is make a print. And then if uh and I'm gonna leave |
|
| 217:52 | on the uh on the document, gonna leave room for you to uh |
|
| 217:57 | your answers with uh uh uh with a pension. So, uh |
|
| 218:06 | there'll be room but you might need room. So that's OK. You |
|
| 218:10 | uh uh um uh um add some pages and you in, you indicate |
|
| 218:16 | the exam, uh please uh see , the, the rest of the |
|
| 218:21 | is on page uh uh uh two something like that. You, you'll |
|
| 218:27 | able to figure it out. So then once you're finished, say |
|
| 218:31 | hours later, five hours later, you're finished, you think? |
|
| 218:35 | I'm, I'm, I can't I've the best I can on it. |
|
| 218:40 | , what you have to do is it and send it to Utah. |
|
| 218:48 | . Yeah. Well, so you're send me only one PDF file from |
|
| 218:52 | of you and then you're gonna say gonna have three PDF files, |
|
| 218:57 | uh, uh, uh, then , when you get all three, |
|
| 219:00 | you send them to me. Um, so, um, |
|
| 219:06 | now, uh, let me ask , have you been uh doing your |
|
| 219:10 | work over there? But you've been listening to, have you learned anything |
|
| 219:14 | this uh uh in this course that didn't know before I do that? |
|
| 219:28 | . Ok. So, uh uh , but even so he's still |
|
| 219:32 | So, uh uh the more you about these things, uh the more |
|
| 219:35 | learn, uh uh and you will more during the exam as you're thinking |
|
| 219:41 | these, uh these uh questions during exam. Uh Some of these ideas |
|
| 219:46 | come into focus for you and you'll , oh, now I understand what |
|
| 219:49 | was saying. Uh uh And uh uh once you do your exam, |
|
| 219:55 | finish it up and, and by way, there's a place on the |
|
| 219:58 | says II I took how much time took? Three hours, five |
|
| 220:03 | 10 hours, whatever. I, really uh uh there's no penalty for |
|
| 220:07 | time you can take as long as want. And uh uh uh normally |
|
| 220:13 | normally find that people who work at longer do better and people who do |
|
| 220:19 | quickly make a, a mistake, they read the question um like |
|
| 220:26 | So some of them are trick So you have to read the question |
|
| 220:32 | and make sure that the answer that answer you're giving is the right |
|
| 220:37 | And by the way, if I a question and there's ambiguous interpretation and |
|
| 220:44 | read it and you say, what this mean uh this or does it |
|
| 220:48 | include this? Should he have said in here? He, he didn't |
|
| 220:51 | always, did he mean always? , if there's a question there, |
|
| 220:57 | you have any, then you write on your exam. I'm not quite |
|
| 221:02 | what this, what you meant I'm gonna assume that you meant to |
|
| 221:05 | always or you, uh uh you meant to say almost always or |
|
| 221:11 | you say. I, that's what , I assume this is gonna uh |
|
| 221:14 | mean? And so as long as make your clarification of my question |
|
| 221:23 | then you get full credit, So suppose I had something else in |
|
| 221:27 | , suppose I didn't mean to say . But you thought I meant |
|
| 221:31 | you answer the question. Uh uh that I was sloppy in the |
|
| 221:38 | you assume I meant always, you write on there. I assume you're |
|
| 221:42 | always. And then I'm gonna I'm gonna grade you on that |
|
| 221:46 | So I'm not gonna penalize you because my sloppiness in writing the questions and |
|
| 221:54 | it's open book, unlimited time is a um, test of your |
|
| 222:01 | It's not, it's not a test your ability to do mathematics, it's |
|
| 222:06 | , it's a test of your So that's why we do it this |
|
| 222:10 | . OK. So that's the way gonna work and uh um, that'll |
|
| 222:19 | . Um, not next week but week after that. Ok. Very |
|
| 222:25 | . So, uh, our time up for today and it's almost |
|
| 222:29 | So, um, I want everybody drive home carefully and so, |
|
| 222:38 | you, you, you can stop recording |
|