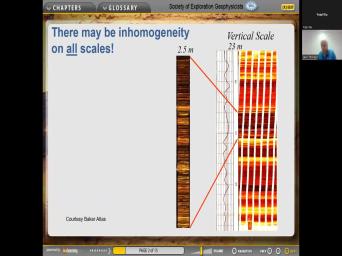
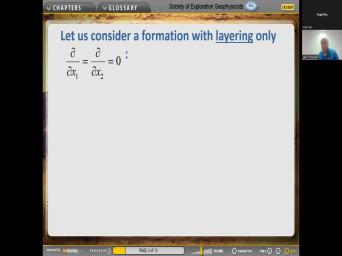
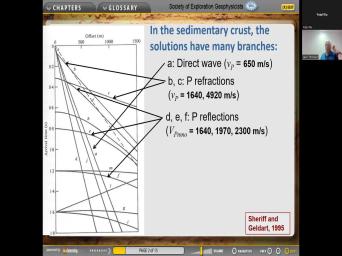
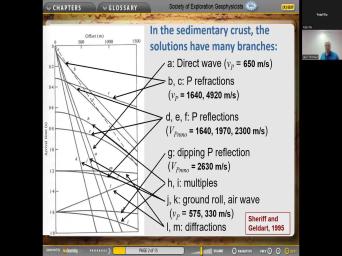
| 00:00 | And so here's Stephanie's question. We you might be interested to hear the |
|
| 00:09 | question. Um It's not about the issues, it's uh geophysics question, |
|
| 00:19 | is your advice to someone who wants be successful in this field? Are |
|
| 00:23 | scared to pursue it because of the of oil? Or is this a |
|
| 00:28 | field? So um um actually I asked a few months ago to give |
|
| 00:36 | lecture to the department on uh what takes to be successful. You tie |
|
| 00:42 | by any chance for you in that , I gave a friday seminar. |
|
| 00:47 | so my advice to the students was lucky. So that's not so easy |
|
| 00:54 | be lucky, but it's not true luck just happens. Uh luck happens |
|
| 00:59 | those who are prepared. And so corollary to that is be prepared so |
|
| 01:06 | when luck happens you're ready for And the way to be prepared to |
|
| 01:10 | a good foundational education. And uh a hedge against the possibility that this |
|
| 01:18 | might be dying. What you want a broad education so that you are |
|
| 01:24 | to uh switch fields later. We we have a lot of students in |
|
| 01:32 | , we're now in computer science because they had the skills and they got |
|
| 01:38 | good job offers from companies wanting those skills and math skills. So you |
|
| 01:45 | sure that you uh acquire those I think you already have pretty good |
|
| 01:51 | skills, but you need to have skills as well and familiarity with how |
|
| 01:56 | handle big data sets. That's one we do in geophysics. We have |
|
| 02:01 | big data sets, but normally they're uh you know, a seismic data |
|
| 02:08 | uh as zillions and zillions of lights it, but it's all structured into |
|
| 02:15 | and receivers and so on. And that's a specialized siphon big data. |
|
| 02:26 | more common our datasets, which are so structured and have a lot of |
|
| 02:35 | in them. Uh just for uh if you want to apply artificial |
|
| 02:45 | to solve a problem, uh So basically what you're looking for is patterns |
|
| 02:50 | data and the human mind is really at detecting patterns and data even when |
|
| 02:57 | lots of distractions for example. Uh , uh here's an example um facial |
|
| 03:10 | . So if I had a Cameron it around the room, the |
|
| 03:13 | uh software and the system will be to recognize two human faces out there |
|
| 03:21 | they're very different faces. But they recognize that you have the characteristics of |
|
| 03:25 | human face, which they and so they can zoom in on you and |
|
| 03:34 | get a detailed look at your face then compare it with their database and |
|
| 03:38 | out who you are. And if a terrorist, uh then they can |
|
| 03:43 | the bell and the cops come and you and don't let you get on |
|
| 03:46 | airplane. That sort of thing happens days. And you know what the |
|
| 03:53 | pattern recognition capabilities really not much advanced when I was your age. We |
|
| 04:01 | knew how to do that sort of . But we didn't have the data |
|
| 04:07 | we didn't have the computers, computers small and slow and expensive. And |
|
| 04:12 | we didn't have the computers to do . So it was not a well |
|
| 04:16 | field. Now it's extremely well developed developing further all the time. Sometimes |
|
| 04:23 | a little bit scary. Uh, intelligence taken over. But remember, |
|
| 04:31 | intelligence is not really that it's a name. It's really a pattern recognition |
|
| 04:37 | large data sets with lots of And uh, those two, those |
|
| 04:44 | two things are new since I was age. Um, uh, but |
|
| 04:51 | can acquire and you should acquire while young, the capability to deal with |
|
| 04:57 | kind of, um, uh, , uh, through machine learning |
|
| 05:06 | uh, machine learning how to recognize . So the first part of your |
|
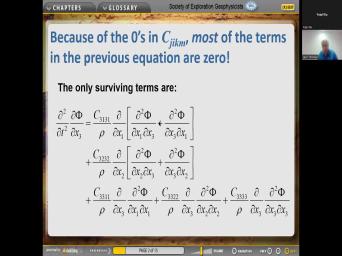
| 05:16 | , uh, advice be lucky and prepared And that's particularly have a good |
|
| 05:23 | , fundamental background in particular math and you can count on during your |
|
| 05:32 | no matter what, where you there's gonna be lots of changes during |
|
| 05:37 | lifetime, in your profession, whatever is. And so you need to |
|
| 05:43 | , keep up with those changes. just tell you a story that my |
|
| 05:49 | was a geophysicist before me, probably why I'm a, physicist. And |
|
| 05:54 | his day, um, uh, recorded the seismic signals on photographic film |
|
| 06:04 | on paper and they analyzed them uh, by spreading those, |
|
| 06:11 | those films, large, large sheets film, they develop them overnight and |
|
| 06:17 | out on the table and uh, to move out things like that with |
|
| 06:25 | drawing tools. And uh, they very low faux, very poor quality |
|
| 06:31 | , but they found a lot of because it was easy to find. |
|
| 06:34 | uh, my father was instrumental in that east texas oilfield, which is |
|
| 06:40 | of the greatest oil fields in the . And um, so you, |
|
| 06:48 | , most of his career, there no computers at all and came into |
|
| 06:52 | field late in his career. And , a lot of his colleagues had |
|
| 07:00 | , you have nothing to do with , but he did. And he |
|
| 07:05 | , he embraced the change and learn to use computers. Of course, |
|
| 07:11 | early computers were nothing compared to over today, but it was a big |
|
| 07:16 | for him and he made it and of his colleagues did. So he |
|
| 07:21 | his job a long time and that he was a very successful oil |
|
| 07:31 | for him for his day. Uh standards were lower than he was highly |
|
| 07:38 | inside his company because when he made recommendation to drill a hole, There |
|
| 07:44 | a 25% chance that it would be success. That was, that was |
|
| 07:50 | success rate and today that would be , uh, terrible if that's what |
|
| 07:58 | did, you would be out of job in two years. Um But |
|
| 08:05 | tools are so much better now that had then and our data is so |
|
| 08:11 | better. So I'm gonna give him pass for that 25% figure. It |
|
| 08:17 | outstanding at the time. And um have moved on. So you've got |
|
| 08:26 | be prepared to move on. Uh ever uh say, well, I'm |
|
| 08:33 | my mid career now. I think can ignore this new development. I'll |
|
| 08:37 | coast through the retirement. That's a attitude. I embrace the change. |
|
| 08:44 | . 2nd part of the question. students scared to pursue geophysics because of |
|
| 08:49 | fluctuation price of oil? Or is a dying field? So the price |
|
| 08:57 | oil has always fluctuated up and And and so I uh Uh I |
|
| 09:06 | I probably saw six or 8 cycles my career. And um I survived |
|
| 09:14 | all by doing my job well. so that's the thing that you want |
|
| 09:19 | do your job well. But I think that um probably, you |
|
| 09:25 | oil is a commodity and the price upon the balance and supply and |
|
| 09:31 | demand is always increasing supplies sometimes gets , sometimes gets behind so that the |
|
| 09:37 | fluctuates. I think we have more than other fields, but all fields |
|
| 09:43 | fluctuations in prospects. So if you stability uh got a government. So |
|
| 09:55 | now, is this a dying Well, it's certainly a changing |
|
| 09:58 | And so the big buzzword this day days energy transition. And uh Professor |
|
| 10:06 | talking about this when he was Um there's a big, there's a |
|
| 10:11 | future for uh solar and for wind and so on. Hydropower, but |
|
| 10:20 | they make up only a small fraction the of need and need is always |
|
| 10:27 | . And so as fast as we convert to uh electric. Uh the |
|
| 10:34 | is good almost as fence. Uh will be demand for oil um for |
|
| 10:42 | for your lifetime. Eventually it's gonna out um probably for your lifetime. |
|
| 10:55 | There will be a large man for while and we simply have to be |
|
| 11:00 | at finding it than we have in past ah over yesterday how, because |
|
| 11:08 | fracking of shales, uh that's led , up until this year we had |
|
| 11:17 | oversupply in the Russian invasion of Ukraine . There's a political decision and suddenly |
|
| 11:25 | uh Russian oil was off the And uh so that meant there was |
|
| 11:31 | shortage and the price went up that's to stabilize in the next couple of |
|
| 11:37 | as other producers step up to make make up the difference. The Saudis |
|
| 11:43 | a lot of spare capacity and we a lot of spare capacity because we |
|
| 11:50 | shut in a lot of coal shell because uh the high supply last |
|
| 11:57 | low price and a lot of wells shut in. So we can uh |
|
| 12:02 | can increase our production also um in short to medium term. But uh |
|
| 12:09 | the long term I think we're gonna to find more oil uh even though |
|
| 12:18 | electric and nuclear are ramping up their from such a low base and the |
|
| 12:24 | is always increasing. So I think demand will be there for a long |
|
| 12:30 | and as it uh finally uh begins find a real shortage. You are |
|
| 12:40 | again to run out of successful discoveries I think the price will go up |
|
| 12:47 | high tech geophysics will be required to the difficult wall remain easy. Oil |
|
| 12:55 | found by by techniques which are really Science and Geophysics has gotten really sophisticated |
|
| 13:08 | the past 30, 40 years. uh like I said yesterday, we |
|
| 13:16 | basically solved the problem of finding oil beneath the complex. Overburden. Haven't |
|
| 13:22 | the problem of how to find the spots of oil production all sales. |
|
| 13:29 | so that um I'm quite confident will solved the next three years and |
|
| 13:35 | you know, by people like us people like you guys, I'm probably |
|
| 13:40 | old for this like in your So, so I don't think it's |
|
| 13:47 | . But you know, there's a that is dying. That's why um |
|
| 13:53 | social students. But what that means that oil companies are going to be |
|
| 14:00 | to find a few students in the , it will bring, oh, |
|
| 14:09 | think it will be high demand for few students in the field, but |
|
| 14:15 | always um always chance to, you , a balance of supply and |
|
| 14:20 | One gets ahead of the other and things happen, the other one gets |
|
| 14:24 | , Bad things happen also. You to be prepared to uh when luck |
|
| 14:31 | your way, be prepared to And that that means getting a good |
|
| 14:40 | education and I think this is part it. Uh This of course is |
|
| 14:44 | a practical course. This is of ideas. And we're about to pick |
|
| 14:50 | the idea of the wave equation, is gonna be implementing what we learned |
|
| 14:56 | about elasticity. So uh this morning will be able to learn how the |
|
| 15:08 | ideas from elasticity leads to the scalar equation for fluids, like uh like |
|
| 15:15 | ocean. And with more realistic assumptions the vector wave equation for uniform, |
|
| 15:21 | should drop solid. Of course the is not like that is not |
|
| 15:26 | it's not ice tropic, but you see that's a step forward. Uh |
|
| 15:32 | as we first derive the equations, not gonna, they're gonna be equations |
|
| 15:37 | how waves propagate, not where they from. And then we have to |
|
| 15:43 | a term in those equations to describe seismic source and that's going to make |
|
| 15:47 | changes. So now we want to that to the earth. So we |
|
| 15:54 | to consider in homogeneous broad formations. then we're gonna look at them uh |
|
| 16:01 | we've developed these equations. Now afterwards gonna look at the solutions. And |
|
| 16:09 | there's a really interesting idea called elastic . And so the last part of |
|
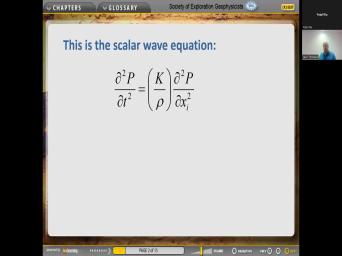
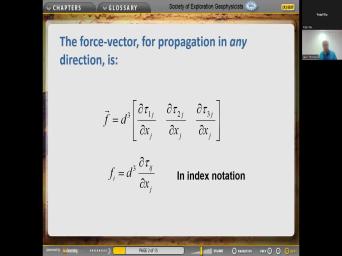
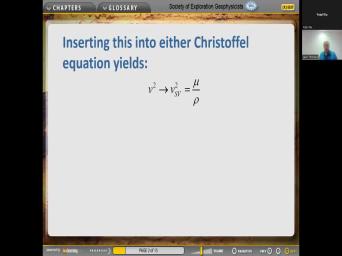
| 16:17 | luxury is about that. Okay, here's the scalar wave equation. So |
|
| 16:24 | have a picture of Isaac Newton and Newton's First law F equals M. |
|
| 16:36 | . This is for and you learned probably when you were a freshman. |
|
| 16:41 | this is for forces on point Well that's not what we need, |
|
| 16:46 | it's the foundation for, we're going recast this for the effects of forces |
|
| 16:52 | continuous bodies. And eventually we're gonna sighting. So we'll start slow from |
|
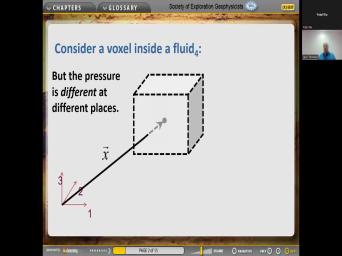
| 17:01 | for fluids. So consider uh volume inside a fluid. And so when |
|
| 17:08 | see a word like this, uh and in uh royal blue colors, |
|
| 17:16 | means that it's in the glossary. if this were uh a live for |
|
| 17:21 | being taught for the scG, it's on this tab right here that would |
|
| 17:26 | up the glossary. You have to a little bit more work. You |
|
| 17:30 | to go to the glossary file which in the uh blackboard in which I |
|
| 17:35 | you have downloaded. And so they're the glossary. It tells you all |
|
| 17:41 | the boxes which of course is a D generalization, the word pixel. |
|
| 17:46 | you know from uh image analysis. it's got a size which we're gonna |
|
| 17:53 | name d. Lowercase D. And the mass is given by the density |
|
| 17:58 | the tube of the to the Okay, inside the fluid there are |
|
| 18:05 | forces and surface forces. So the forces are like gravity and so they |
|
| 18:11 | everywhere uh on the inside of Um Now uh in Iraq in the |
|
| 18:21 | or let's get that uh in a in the ocean gravity is pointing |
|
| 18:30 | And so it's uh all the But it's constant and it's and it's |
|
| 18:36 | by a constant pressure from below. gravity is pulling down, pressure is |
|
| 18:43 | up from below. That's a surface . Uh And so those cancel. |
|
| 18:48 | then furthermore uh there's pressure on all but those are constant. So we're |
|
| 18:56 | ignore these constant forces. We're going consider only variable forces. Now we're |
|
| 19:04 | locate this rock still at a position is measured from the origin recorded. |
|
| 19:10 | we established an origin over here and we have a vector to the center |
|
| 19:16 | the box in. And so that that that's the vector X. And |
|
| 19:21 | tells where the where the box will the pressure at the center of this |
|
| 19:28 | is P. F. X. it's different at different places for example |
|
| 19:36 | the top surface uh that there is displacement. Uh There is a a |
|
| 19:46 | uh vector uh delta X. Which given by uh 00 at D. |
|
| 19:56 | . R. Two is the uh the difference between this position and this |
|
| 20:05 | . So the pressure is the pressure X. Plus that uh delta |
|
| 20:14 | And on the bottom it's uh corresponding expression except that there's a minus B |
|
| 20:22 | two and on the side uh it's different again because the difference vector is |
|
| 20:33 | zero for two in the one position this thing. Here it is on |
|
| 20:38 | other side with a minus D. then front back. Uh Same. |
|
| 20:45 | the corresponding forces for all these are pressure times the area. Okay? |
|
| 20:54 | here this is a force In the directions at the top and here is |
|
| 21:07 | force right down here is a force the three direction at the bottom, |
|
| 21:11 | see that. And uh correspondent here the force in the one direction from |
|
| 21:17 | right one and here's the one for direction from the left. So we're |
|
| 21:24 | up all these um uh forces on surface of the box and then we |
|
| 21:32 | sum them up. So this looks a make it but it's not it's |
|
| 21:36 | six terms equations. And it's arranged that the top row is the right |
|
| 21:42 | left and the bottom row is the and bottom and the middle row is |
|
| 21:47 | back. And they all have this D squared here given the size of |
|
| 21:55 | Vauxhall. And you see there's there's minus science scattered around uh multiplying by |
|
| 22:01 | pressure and then there's various minus signs indicating the positions. And uh if |
|
| 22:09 | look back previous slides to see where those came from. So let's consider |
|
| 22:16 | sound wave traveling vertical. So the does not vary in the horizontal |
|
| 22:21 | So these top two roads are zero so this is all we have |
|
| 22:29 | So um basically it's constant pressure equal out on now since the box was |
|
| 22:44 | house, what the small means means compared to the wavelength of sound. |
|
| 22:49 | can describe this pressure. This pressure with the taylor expansion. And uh |
|
| 22:57 | pressure at this place here is given the pressure at the center plus this |
|
| 23:04 | series uh change and uh thinking about whether this is the right derivative to |
|
| 23:19 | um go back and and this is fact the and furthermore notice that it's |
|
| 23:27 | at the center. It was evaluated . And this is the difference in |
|
| 23:35 | from um pressure here at the top or two away from the middle. |
|
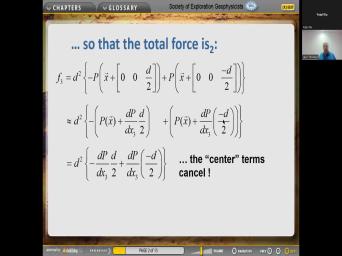
| 23:45 | then the total force is uh given . Now let me see, let |
|
| 23:50 | check here when a word like that that I'm not not sure whether or |
|
| 23:55 | that's a live link but I'm gonna at. Yeah so it took me |
|
| 23:59 | here so to be frank here, not sure whether uh Back in the |
|
| 24:10 | or not. I'm gonna page forward slide. Yeah. So it took |
|
| 24:14 | back to the uh that place and now here we are back and this |
|
| 24:20 | me that changes colors uh reminds me did that before. So I'm gonna |
|
| 24:26 | forward for the animation. And so we put in the taylor expansions for |
|
| 24:31 | two uh figures top and bottom and see more minus signs coming in and |
|
| 24:42 | the center terms cancel. And we're with only the taylor expansion terms. |
|
| 24:50 | we collect terms and we come out this. So um it's you can |
|
| 24:55 | that it's easy to make mistakes here of skipping out a minus sign. |
|
| 25:01 | I assure you that this is all correctly. And notice that we now |
|
| 25:07 | d cubed here. So we start with the squared, but then we |
|
| 25:12 | a. D. Coming in because the taylor expansion thing. And that's |
|
| 25:17 | now we have the view. Remember this is far more vertically traveling wave |
|
| 25:24 | the ocean. So we're gonna put into the equation of motion. So |
|
| 25:31 | only a force in the three And this is what we just |
|
| 25:35 | And uh so on on the right of Newton's first law says uh mass |
|
| 25:43 | acceleration. So we're gonna call the in the three direction and simply rearranging |
|
| 25:51 | we find that the acceleration is given minus one over road, where did |
|
| 25:57 | road come from? Well, remember the mass is given by road |
|
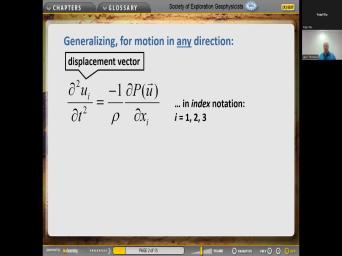
| 26:01 | Youtube canceled out. So we're left this, that's the acceleration in terms |
|
| 26:09 | the pressure gradient. Now, because the machinery that we set up |
|
| 26:15 | it's easy to uh to change that any uh direction. Always say is |
|
| 26:24 | the acceleration now looks like this secondary respect to time of a displacement vector |
|
| 26:31 | here's the highest component. So we that equal b 12 or three. |
|
| 26:35 | we've been going in any direction and course we have to put on here |
|
| 26:40 | same direction from the gradient. And we um uh we recognized that this |
|
| 26:52 | this derivative is a gradient operator. so um uh we use this notation |
|
| 27:01 | the bill all del symbol to indicate derivative. That's okay. Now remind |
|
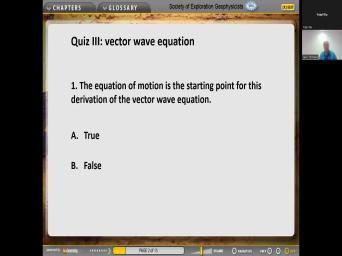
| 27:12 | that it is only in the So I wish is this true or |
|
| 27:22 | ? The equation of motion is the point for this derivation. I will |
|
| 27:27 | away reclaiming, raise your emotion. didn't actually say that did I said |
|
| 27:35 | was uh it was first long but the answer to this is true. |
|
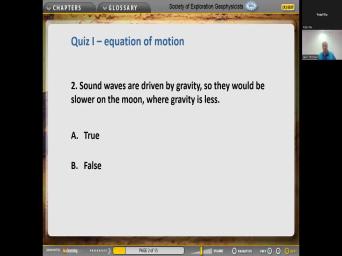
| 27:50 | . Sound wave or false. Sound are driven by gravity. So they |
|
| 27:54 | be slower on the moon or gravity less. Say it again. |
|
| 28:07 | uh that's true, but this is in space is on the moon. |
|
| 28:12 | is talking about a sound in wound where the gravity is less because, |
|
| 28:22 | you have to decide, Well it's that the gravity is less on the |
|
| 28:35 | expression. I think this is Yeah, that's fishing. I'm not |
|
| 28:47 | think that. Well is it true sound waves are driven by gravity? |
|
| 29:00 | is a body force, its uh operating throughout the throughout the box ill |
|
| 29:08 | it gets canceled by constant since gravity constant, it's constant in time. |
|
| 29:14 | mean it's canceled by uh by variant pressures. And so that's not |
|
| 29:22 | to lead to waves. So we ignore that. What we found was |
|
| 29:26 | uh um the motion of the particles this box are driven by pressure gradients |
|
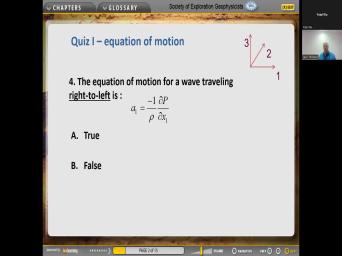
| 29:40 | in the center. Okay. Now see if you can figure out the |
|
| 29:46 | um Oh bookkeeping here. Um So have uh we have the coordinates are |
|
| 29:59 | here and uh the question is about left center of the box. So |
|
| 30:05 | means left in the one direction. which of these? Uh is |
|
| 30:15 | Yeah, that's right because this is left center, this would be the |
|
| 30:19 | center and this would be uh the and this would be the bank. |
|
| 30:27 | . Yeah, you're right. So now I didn't I didn't um |
|
| 30:36 | you this but I taught you enough that you can figure this out. |
|
| 30:41 | is uh is this the right equation motion for a way of traveling right |
|
| 30:47 | left, remember what we did was drive up and down? But now |
|
| 30:51 | asking right and left, right, to left. So is this the |
|
| 30:56 | equation of motion for that? Yeah it's accelerating in the one direction and |
|
| 31:06 | depends upon this uh primitive in the . Direction, in the one |
|
| 31:15 | Now. Uh can you tell from ? How about the opposite left to |
|
| 31:23 | ? Let me see here. Uh that that that's not uh on the |
|
| 31:29 | quiz but think about it. Uh this the right equation we already |
|
| 31:36 | Yes, you're correct. That that's pressure right to left. How about |
|
| 31:40 | to right? Is this the right for something traveling left to right? |
|
| 31:49 | . Right. All you do is that case this is gonna be a |
|
| 31:52 | number and uh this is also gonna negative. So uh so that uh |
|
| 32:02 | very good uh you were able to to answer the answer, answer the |
|
| 32:09 | properly even though I didn't teach you answer because you were able to |
|
| 32:14 | but I did teach you to this . So that's the uh um crucial |
|
| 32:26 | skill which not everybody has. I'm to see that you have. Okay |
|
| 32:32 | let's convert these uh vector equations, is affect right, we're gonna take |
|
| 32:40 | divergence of this. So that means we're gonna uh operate on both sides |
|
| 32:46 | the operator D by dx i uh . Now we have repeated indices |
|
| 32:54 | and in vector notation, it looks this and an index notation looks like |
|
| 33:00 | . And you know what we're going do is we are going to um |
|
| 33:06 | move the derivatives around uh through those on the next slot here is here |
|
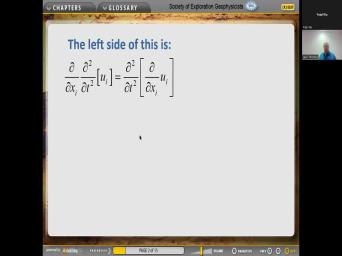
| 33:15 | the left side of the equation. go back here. So we're gonna |
|
| 33:18 | about this here and the left side like this. It's just put the |
|
| 33:27 | , displacement in its own little square . And then we know in our |
|
| 33:32 | calculus we can interchange the order of , so we bring the derivative with |
|
| 33:38 | to X. Inside here, all way inside here. And then we |
|
| 33:45 | that this is the strain in it's the sum of uh of uh |
|
| 33:55 | stream components epsilon II because we are over all eyes here and we know |
|
| 34:04 | previously that's the dilatation, that biometric . So remember the volumetric changes given |
|
| 34:13 | the in compressibility in this way. let's just see what happens when we |
|
| 34:20 | click here, cannot open the specified . So this only worked for in |
|
| 34:27 | scG environment. So now putting this together. Uh the left side of |
|
| 34:37 | equation now has pressure in here and compressibility has got an extra minus sign |
|
| 34:45 | you didn't have before, that came right here, but it's still got |
|
| 34:49 | acceleration operator on the outside. So we've put together both sides of the |
|
| 34:57 | . And uh now it looks like . And you know what we're gonna |
|
| 35:02 | next? We're going to assume that pressure is uh uniform. So that |
|
| 35:12 | that we can uh bring this I said it wrong that we're going |
|
| 35:17 | assume that the density is uniform so we can bring the density outside of |
|
| 35:22 | operator. You did it. So we have on the left a derivative |
|
| 35:30 | pressure to directors respected time of pressure on the right to directors of pressure |
|
| 35:37 | respect to position and some conscience outside make the units match up and saw |
|
| 35:47 | uh bring the K to the right . Remember we had this minus |
|
| 35:54 | Let's see what we reported this, we minus sign on both sides. |
|
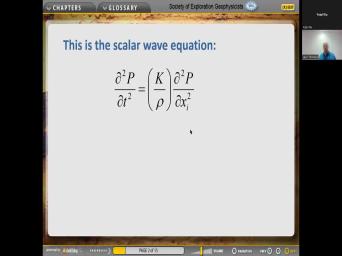
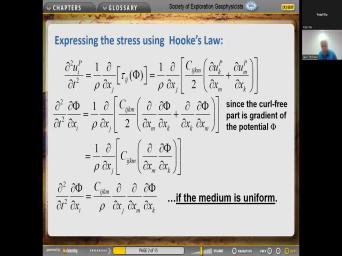
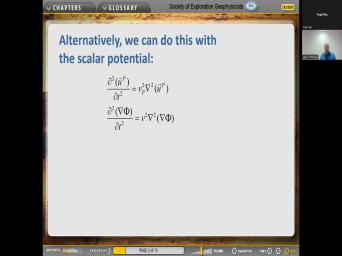
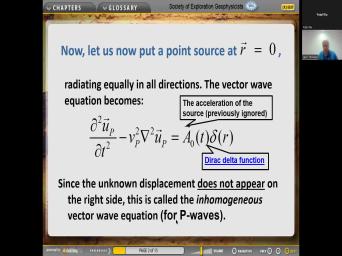
| 36:22 | is now what we call the scalar equation so that the unknown in this |
|
| 36:28 | pressure. And so when we have marine seismic survey, what we do |
|
| 36:34 | measure the incoming uh seismic waves with , not geophones, but hydrophones. |
|
| 36:42 | measure fluctuations of pressure. And it's quite remarkable how they do this. |
|
| 36:50 | to be frank. I am not how those clever engineers have done |
|
| 36:55 | but they've made a little package which can sell uh for just a couple |
|
| 37:01 | $100 makes a hydrophone and they have dozens or hundreds of these on a |
|
| 37:09 | and they have multiple streamers. Maybe geophones in the water at one |
|
| 37:15 | And the boat is pulling it forward the waves are sloshing around and the |
|
| 37:20 | are sloshing around. And even despite those voices. And despite the |
|
| 37:29 | construction of this hydrophone, it's able measure the tiny, tiny fluctuations of |
|
| 37:33 | sensitive waves which come into it. you think that's remarkable? Now, |
|
| 37:40 | seismologist? They don't, uh, , well these days they do, |
|
| 37:44 | in my day they never, when was your age, they never did |
|
| 37:49 | kind of stuff when they were looking earthquake ways. They would always have |
|
| 37:55 | instrument on land in a cave or a tunnel or something like that, |
|
| 38:01 | , protected from the noises and very , many thousands of dollars for each |
|
| 38:09 | . And of course they're measuring three components. But uh, it was |
|
| 38:15 | and it was specialized and it was and there weren't very many of |
|
| 38:20 | So these days they do much better they're looking for earthquake signals. |
|
| 38:27 | and they, but still, they have dedicated systems. Let's measure |
|
| 38:38 | In fact, we have one of uh, stations right here on |
|
| 38:42 | Are you familiar with that one, uh, just across the road |
|
| 38:48 | just across the road, uh, the Georgia building and uh, |
|
| 38:57 | satellite cafeteria, There is a seismic and it's in a lockbox, so |
|
| 39:06 | people don't screw around with it. uh there are people here in our |
|
| 39:11 | who uh the data from that and , make sure it's always working. |
|
| 39:16 | that's a very sensitive instrument which is uh extra equation and Taiwan. Um |
|
| 39:30 | it's it's uh it's expensive several $1000 that. You couldn't possibly do that |
|
| 39:38 | uh exploration seismic because we need to many more receivers. That's secret to |
|
| 39:46 | success is lots of receivers, lots source position, lots of receiver |
|
| 39:52 | So they've got to be cheap and have succeeded in making a very cheap |
|
| 40:01 | and also cheap earphones which nevertheless sensitive to measure these very tiny oscillations. |
|
| 40:12 | uh seismic sources, What more about magnitude of those uh perturbations later. |
|
| 40:22 | in the wave equations we have 22 with respect to time to to produce |
|
| 40:28 | to position and a proportionality concept. uh Stephanie, tell me what, |
|
| 40:37 | is the physical dimensions of that proportionality . K overrun. Well, I |
|
| 40:51 | want to know the magnitude of I want to know the physical dimensions |
|
| 40:56 | it. We have to have the physical dimensions on both sides of the |
|
| 41:01 | . So this is pressure divided by square of time. Right? So |
|
| 41:06 | is pressure divided by the square of and um physical units. And so |
|
| 41:15 | make these work out what, what this got, What got me the |
|
| 41:19 | dimensions of this ratio K. Overall don't know what K is and you |
|
| 41:25 | don't know what row is. I you know that rho is mass per |
|
| 41:29 | mass per unit volume but I'll bet uh uh you're not quite sure what |
|
| 41:37 | is but you know we can figure out. So let's go back |
|
| 41:41 | Okay so uh notation is dimensions and can see that clearly right here. |
|
| 41:50 | Kay must have the dimensions oppression uh order for the left side of |
|
| 41:59 | So the right side has to be . So Kay must have the dimensions |
|
| 42:03 | pressure we're gonna go for. So we have pressure divided by density. |
|
| 42:08 | What does that what what does that out to in terms of time and |
|
| 42:21 | ? You don't really have to uh think you're you're thinking about this in |
|
| 42:28 | wrong way. Uh Caro has to the physical dimension to make the physical |
|
| 42:37 | on the right side the same as on the left side. So uh |
|
| 42:42 | that equal to only have to have squared over T squared? Yeah, |
|
| 42:49 | . And see without working out this pressure. And this is uh densities |
|
| 42:55 | working out uh in detail which each those means. And then taking the |
|
| 43:01 | you can see immediately that the ratio got to be expert over t |
|
| 43:10 | So X squared over two squared is the dimensions of velocity squared. |
|
| 43:17 | so this thing has to have conventions velocity square. Okay, so uh |
|
| 43:24 | notation around, you recognize how changes notice how we slipped in here. |
|
| 43:30 | Del square. And so in Cartesian uh this uh second quarter derivative respect |
|
| 43:40 | X. I. It's the same as a Gaussian operator doll sprague. |
|
| 43:47 | notation which we talked about yesterday, can check it, check it uh |
|
| 43:52 | the files that you have. so just like you said, it |
|
| 43:57 | the dimensions of of exo routine which is velocity squared. So let's |
|
| 44:04 | give that a name. Uh We'll this instead of calling the Contin. |
|
| 44:11 | call it V square. It's a and we don't know yet what is |
|
| 44:18 | velocity of. But uh it's a good guess that that is gonna be |
|
| 44:22 | velocity of the wave. So here's scalar wave equation. Yeah, if |
|
| 44:34 | wanted to we could write it in of facilitation, uh just make this |
|
| 44:40 | and things cancel out and uh get same equation in terms of the rotation |
|
| 44:48 | continue to analyze the pressure version. mention this because when we go to |
|
| 44:54 | vector wave equation, we're gonna be about strains, non stress. And |
|
| 45:00 | mhm. This is a strength. is the volumetric strength and however it's |
|
| 45:07 | in talking about the scalar wave of the discussion in this farm unknown as |
|
| 45:18 | . So, so now let's go to the simple case of wave traveling |
|
| 45:24 | so that so instead of having a operator here, we have only the |
|
| 45:30 | really respect. See now think about , whatever the solution is, it's |
|
| 45:40 | be a solution varying with temperature and and it's gonna whatever it is. |
|
| 45:49 | It's got to be very in this uh combination which we call the phase |
|
| 45:55 | with five written like that. The is a function of time and space |
|
| 46:01 | it depends upon time like this and like this and Parameter Omega and another |
|
| 46:11 | K three. So we will talk about those parameters charts. Okay, |
|
| 46:19 | recognize the uh the parameter omega is notation for the angular frequency. So |
|
| 46:27 | we talk about the cyclical frequency, cycles per second, that's f. |
|
| 46:34 | radiance per second is 25 times. we have a name for this uh |
|
| 46:43 | three. I see the arrows pointed the wrong place to adjust that. |
|
| 46:49 | three is called the vertical wave It's gonna be related to the wavelength |
|
| 46:58 | three itself is vertical way of Now, you might have your doubts |
|
| 47:04 | whether what I said back here. true. It's really true that the |
|
| 47:12 | only uh can't be random combinations of and space, but only through this |
|
| 47:21 | . So let's just test that the side of this. So what we |
|
| 47:24 | is pressure is not really independently not really independently varying with time and |
|
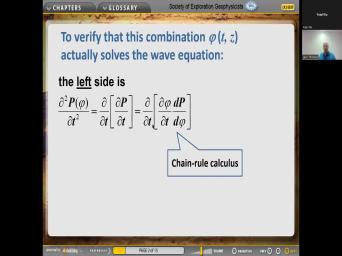
| 47:33 | but only through the phase. So write the pressure depends on the face |
|
| 47:39 | respect to uh Second review of pressure respect to time looks like this since |
|
| 47:48 | uh pressure only uh depends upon We uh we use the rules of |
|
| 47:56 | to uh show the derivative of pressure respect to phase right here and the |
|
| 48:01 | of phase with respect to time Chain rule, cackles, Stephanie, |
|
| 48:07 | you comfortable with that? Okay, . Uh use that kind of stuff |
|
| 48:17 | the time. And so uh the with respect to uh phase respect the |
|
| 48:26 | is just omega from the previous And then we do it again with |
|
| 48:30 | diverted as we get omega squared times second order of P with respect to |
|
| 48:37 | black wise, the right side of equation work through the same kind of |
|
| 48:41 | . And and you find that uh right side is the square times K |
|
| 48:46 | square, where does the K three from comes from these derivatives of phase |
|
| 48:52 | respect to position. And this is for either plus or minus Value for |
|
| 49:00 | three. So now the right side the left side. If and only |
|
| 49:09 | we have this relationship here between a and omega and V. Yeah. |
|
| 49:21 | , so now we are set up consider um solution. Louise. And |
|
| 49:30 | I'm gonna propose that um the solution uh no I'm gonna I'm gonna suggest |
|
| 49:49 | a solution. Is this So uh have pressure as a general function of |
|
| 49:57 | Let's say. Okay so how about function of five? Which is |
|
| 50:00 | oiler number eight uh to uh to power I. So this will |
|
| 50:11 | Uh we're gonna show that this works but any function five will work as |
|
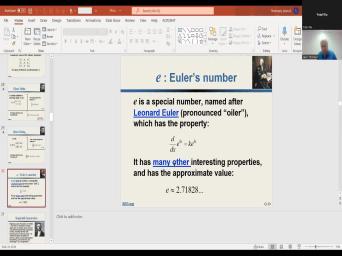
| 50:18 | solution for pressure. So right here making sure you know about oilers number |
|
| 50:25 | . And uh Complex number I is as a square motive -1. So |
|
| 50:34 | talked about that um Good. Yesterday is really crucial for uh first |
|
| 50:44 | Number A is a special number kind like pop and it was, it |
|
| 50:51 | discovered by Oiler And it's a natural . It's a number of a little |
|
| 50:58 | smaller than pie. It's about 2.7 . And it's like it uh is |
|
| 51:05 | irrational number and uh decimal representation. goes on forever Box Mix in |
|
| 51:17 | And it has some special properties which described in the glossary will encounter those |
|
| 51:24 | party player. Now the next idea uh now this is really a complex |
|
| 51:37 | . I think that there's a special like pi which comes which is needed |
|
| 51:43 | describing circles examined. That's a big which you learned in trigonometry I |
|
| 51:51 | Um I suppose in high school that triggered on about pie in high school |
|
| 51:59 | I'll bet you didn't learn about about father's number eight finally learned about |
|
| 52:05 | Number a calculus. Um and uh are there are a few magic numbers |
|
| 52:18 | that, but only a few. kind of a mystery why we don't |
|
| 52:23 | lots of special number like but we only a few. And uh they |
|
| 52:31 | remarkable properties and I encourage you to the glossary number eight tonight. |
|
| 52:47 | I'm sure you have already uh learned those properties in your past forces. |
|
| 52:55 | won't hurt to have a Now we in here complex number in the exponent |
|
| 53:10 | vegan. And what that means is right side of this. Look at |
|
| 53:17 | uh All right. The right this middle party, not the right |
|
| 53:24 | but the middle part is a complex because of this. I and this |
|
| 53:29 | also a complex number. So the has to be a complex number |
|
| 53:35 | But you know that pressure is not complex number. Pressure is a real |
|
| 53:41 | measure. And you can feel it your hands and stuff like that. |
|
| 53:45 | , uh it's always makes a puzzle students think how can we be |
|
| 53:53 | how can we be saying that solution a real property? Like pressure has |
|
| 54:01 | numbers in we're gonna be measuring pressure a real instrument and it's a real |
|
| 54:08 | and it doesn't know anything about complex . And so the answer to this |
|
| 54:18 | is um that uh just at this it's an inconsistency and you have to |
|
| 54:29 | faith that uh we talked about Uh actual thank you your time. Um |
|
| 54:52 | I like. So whenever we have equation like this because and better mind |
|
| 55:13 | with it. Oh. Mhm. the time we get to particular problem |
|
| 56:05 | , your number for the plane wave that we have here, it has |
|
| 56:20 | wavelength which I'm gonna give is uppercase with a subscript three. To remind |
|
| 56:26 | we're talking about vertical propagation here. I think you know that the wavelength |
|
| 56:36 | given by the velocity over the the cyclical frequency. So we put |
|
| 56:41 | here the angular frequency that brings in two pot. And so uh this |
|
| 56:48 | of V over omega is K three or minus. Now I mentioned this |
|
| 57:02 | solution because it's gonna be very useful us. Uh we're gonna be able |
|
| 57:10 | um construct solution for any problem by of terms like this. So we |
|
| 57:24 | to think more about uh about this my solution. So let's make another |
|
| 57:40 | . Of course, you're gonna rewrite face by factoring out the uh omega |
|
| 57:46 | this. And uh then let's think whether uh we have one, let's |
|
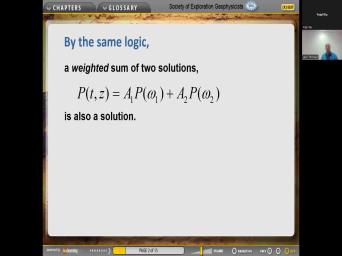
| 57:55 | we have a solution for any So, and we don't yet know |
|
| 58:01 | omega is but uh we call it frequency. We know that waves have |
|
| 58:06 | of different frequencies. So let's assume we have one solution with one angular |
|
| 58:12 | and then a separate solutions to to angular a second angular frequency and then |
|
| 58:19 | we're going to guess that the sum also a solution. So you can |
|
| 58:28 | for yourself this is true. Um so this happens because the wave equation |
|
| 58:34 | linear, it means that the unknown appears for the first time ve uh |
|
| 58:44 | there's in they're a v squared, squared is obviously not linear, but |
|
| 58:47 | unknown is linear. It's the pressure of the first power on both sides |
|
| 58:54 | the equation. By the same We can have a weighted something to |
|
| 59:01 | . That's also a solution that's uh obvious to you. But if it's |
|
| 59:05 | obvious, you can work it out just make sure to yourself that perhaps |
|
| 59:17 | a solution. So that's an important . Does not seem like a trivial |
|
| 59:24 | doesn't work because what it implies is we can take a plane wave |
|
| 59:29 | different frequencies and different uh amplitudes and add them up, um weights which |
|
| 59:40 | specially chosen to solve any problem. fact here, of course, is |
|
| 59:47 | we have many times, not just just sums of two, but sums |
|
| 59:51 | many. And these can be an number of frequencies. These coefficients are |
|
| 59:59 | to be determined by initial conditions and boundary conditions, for example, uh |
|
| 60:05 | conditions, uh depending on whether the is a strong source or weak source |
|
| 60:11 | gonna affect these. Uh We decide these A's and uh then we have |
|
| 60:19 | decide about boundary condition. For there might be a free surface at |
|
| 60:24 | surface, might be no boundary at bottom. Uh All those things are |
|
| 60:33 | help us decide These values of Now that's all for a vertical population |
|
| 60:43 | of the mathematical machinery that we set yesterday. It's easy to generalize uh |
|
| 60:53 | to any direction. And all you to do is recognize here that uh |
|
| 60:59 | eye is a subscript I is So we're summing over all eyes. |
|
| 61:08 | then uh since we're gonna be considering directions, we have to generalize the |
|
| 61:21 | of face. So instead of K times e it's a vector dotted with |
|
| 61:29 | and for any solution uh He is function of five on the left |
|
| 61:35 | Uh We have, instead of a , respected time, we have rivers |
|
| 61:41 | to by and uh as a we have these two factors of omega |
|
| 61:50 | out and a similar thing on the side, two factors of K. |
|
| 61:55 | . So now they are multiplying this and you can see this same narrative |
|
| 62:03 | both sides. So that what that is that uh this product K 11 |
|
| 62:12 | plus K +22 squared plus K K square as K two square. K |
|
| 62:18 | square. Uh That's the length that's the square of the length of |
|
| 62:24 | vector K. And so um um will be satisfied if K. Is |
|
| 62:34 | to vega Plus or -1 over So, here's a little question. |
|
| 62:50 | We have a list here. Look the bottom of the list that says |
|
| 62:54 | only two and answer is all of attributes above. And so now what |
|
| 63:00 | need to do is you scan through and see which ones those are |
|
| 63:05 | And then the right answer is gonna uh Probably your your f. So |
|
| 63:14 | it's definitely does it have um Remember talking about the scalar wave equation but |
|
| 63:21 | favorite, Not the equation of Um Does it have to do with |
|
| 63:27 | to time? And how about B. Is that true? How |
|
| 63:32 | C. Is that true? Unknown appears to the first power only. |
|
| 63:41 | the unknown function so far? Uh The unknown function is the |
|
| 63:50 | So, she is also true. d a single parameter which describes the |
|
| 64:00 | . That's also true. And that's philosophy square. Uh So it has |
|
| 64:05 | the attributes above. So that's that's . Uh So it can be written |
|
| 64:12 | with either pressure or dilatation as the function false. It's the same |
|
| 64:31 | Question three. It's only valid for in vertical direction since fluids only vary |
|
| 64:37 | the vertical direction. Is that Yeah, that's false. Uh Number |
|
| 64:44 | uh fluids very uh more than the direction. Uh but they do very |
|
| 64:51 | in the vertical direction. Might not aware of this, it's common for |
|
| 64:55 | to think of the ocean as the velocity everywhere, but that's not |
|
| 65:01 | The velocity varies with depth in the because of increasing pressure and decreasing temperature |
|
| 65:10 | also changing salinity. So uh velocity sound and water changes its function of |
|
| 65:23 | , and also it changes laterally. example, in the gulf of |
|
| 65:27 | we have uh it's quite prominent dr , but let me uh introduce that |
|
| 65:43 | idea. You know about the Gulfstream goes up the east coast of |
|
| 65:48 | United States, turns to the east then goes south uh along europe. |
|
| 65:56 | uh um it's pretty obvious, it be intuitively obvious that uh profiles of |
|
| 66:08 | temperature and salinity are different in the stream than they are in the middle |
|
| 66:15 | the atlantic. So uh that means the velocity of sound and water checking |
|
| 66:22 | . Uh picking up on the idea I said before, there are features |
|
| 66:29 | eddies which are circular um uh secular patterns, water which uh move around |
|
| 66:39 | the gulf of Mexico. And in large closed bodies also. And they |
|
| 66:47 | you can have circular motions of the of uh something like, I don't |
|
| 66:56 | 1/10 of a meter per second, like that pretty fast folks. And |
|
| 67:04 | generally rotate uh clock wanders around and they affect the fish and they affect |
|
| 67:13 | navigation affect the oil platforms that are there. And uh it's all quite |
|
| 67:20 | complicated things like weather in, in the ocean, whether inside the water |
|
| 67:29 | the ocean, uh and of course velocity of sound inside those eddies is |
|
| 67:38 | than outside. The some cases actually reflections of sound off the boundaries. |
|
| 67:56 | , off the horizontal boundaries of slim and temperature in the ocean. You |
|
| 68:03 | see that the right experiment. You sound reflecting of uh interior boundaries inside |
|
| 68:15 | ocean. And there are people who . And then finally, I want |
|
| 68:23 | say um oh, another point making come back, go on a |
|
| 68:53 | Um Stephanie is this trip? If have 17 different solutions and waves or |
|
| 69:03 | , this is some also solution. . So that's really important. So |
|
| 69:08 | example, if you have a a of coming this way and a way |
|
| 69:11 | coming this way when they cross, just means that there's still a solution |
|
| 69:16 | they don't uh uh it is passed each other. They don't uh |
|
| 69:23 | they don't do this, they pass each other. And of course there |
|
| 69:28 | ways going in all directions all the inside the earth. So that's really |
|
| 69:35 | that as they pass through as they each other, they they don't change |
|
| 69:45 | all. They just add together and pass on. Really important feature comes |
|
| 69:53 | of the linearity. Yeah, all is for uh water waves uh waterways |
|
| 70:03 | that makes you way sound waves in water. I want really. That's |
|
| 70:17 | for us, especially for marine surveys really what we want to know is |
|
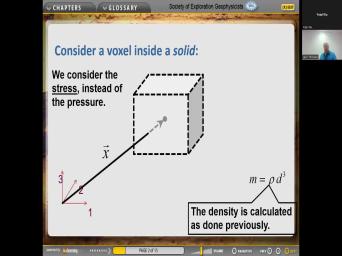
| 70:23 | and rocks. So that's called the waving. So go back to the |
|
| 70:28 | salt. Now we have a box the song and we're going to consider |
|
| 70:34 | stress instead of the pressure. Remember is a tensor. Okay, density |
|
| 70:41 | the same way location of the various Hello, various sides is the |
|
| 70:53 | And so here is distress at the of the box. We call it |
|
| 70:59 | component three J. So there's there's Jacobs 123 here, but it's because |
|
| 71:09 | top of it is has a uh the unit vector pointing in in the |
|
| 71:15 | direction. Uh that's gonna that's why have the three here. Remember tao |
|
| 71:21 | two indices. And so the first is gonna be a three on thinking |
|
| 71:26 | the top. But this is a equations, we've got the forces can |
|
| 71:31 | oriented in any direction 12 or but they're all going to be located |
|
| 71:36 | this position. Okay. And here's bottom. And so the only thing |
|
| 71:44 | about this is the location vector Here the side that you see now because |
|
| 71:52 | unit area is pointed in the one we're talking about how one J. |
|
| 71:58 | then on the other side again, won Jae but with a different position |
|
| 72:03 | up in the bottom, see this tau to J here. And so |
|
| 72:09 | corresponding forces are those stresses times the area. And now we have now |
|
| 72:21 | have uh various minus signs here minus here and a minus sign here, |
|
| 72:28 | minus sign here. And that's because force is directed upwards here and the |
|
| 72:34 | is directed downwards here. Oh all forces are carefully designated with minus signs |
|
| 72:52 | in the right places and not in wrong places. And also why on |
|
| 72:58 | I did this right, so that we add them all up and |
|
| 73:02 | this is a simple addition looks like matrix, but it's a simple edition |
|
| 73:07 | you see the minus signs of appearing some places here and not others. |
|
| 73:11 | so uh let's see what happens when compare with the scalar case. |
|
| 73:17 | so here is the scalar case uh it's got pressures instead of stresses but |
|
| 73:24 | um lots of similarities here. Now myself back, that's true. Enter |
|
| 73:43 | not have done that. Okay, um now we have stresses transmitted across |
|
| 74:02 | six faces. So the index one the direction of the, of the |
|
| 74:11 | . These are uh faces right in lap. Now 1, 3 here |
|
| 74:17 | one per year and then front and has uh different direction, direction. |
|
| 74:28 | the threes indicate the direction of the . And so this is all for |
|
| 74:35 | in the three directions. So you uh this is uh like a sheer |
|
| 74:45 | . It's got the forces are pointing the three directions And the unit areas |
|
| 74:52 | in the one direction. All of have forces pointed in the three |
|
| 74:58 | Some of them are shear stresses and of them are uh compression stresses, |
|
| 75:05 | example, here's the compression of stress here. There you go. Second |
|
| 75:21 | . Oh, okay, good news my wife. So this is, |
|
| 75:41 | , so I shouldn't have clicked The comparison with the scalar case is |
|
| 75:46 | here. Now let's specialize this vector for a wave traveling growth. So |
|
| 75:59 | that means that we can uh forced cancel out on the on all the |
|
| 76:06 | . And except for the this is similar to what we had from pressure |
|
| 76:14 | in the ocean as before. We're to use your tailor uh approximation two |
|
| 76:25 | days. And uh so after going the manipulation, same as we did |
|
| 76:36 | for the pressures, we find out the force in the three direction is |
|
| 76:41 | by uh this three greeting Uh down , 3. So that's uh for |
|
| 76:53 | vertically traveling. And then it's trivial generalize that for full force vector and |
|
| 77:10 | is only the force vector and the components of them. Of course, |
|
| 77:16 | the other uh the other components are here. Remember this is still vertical |
|
| 77:22 | only. So these are all vertical Forces in all three directions. |
|
| 77:34 | 2, 3 Stress only on the . three planes because this is vertical |
|
| 77:42 | . And uh considering only various in X. So uh further it's easy |
|
| 77:52 | generalize for any direction. That's all do is uh change the threes to |
|
| 78:00 | and uh some over J. And an index notation uh which is simpler |
|
| 78:10 | . So this is a vector equation for three components. Let's look at |
|
| 78:19 | one at a time when we call the ice component and it's equal to |
|
| 78:24 | J uh J derivative of the J the IJ component of town. This |
|
| 78:33 | almost trivial to to uh generalize like because of the machinery we've set up |
|
| 78:42 | . Remember that because jay is We're summing over these. And so |
|
| 78:50 | riding through by the right watch, that. Yeah, force provided by |
|
| 79:07 | . Q. Is given by the of the stress. First per unit |
|
| 79:17 | is equal radiant after stress. Now into the equation of motion. Just |
|
| 79:23 | we did for uh uh motion What we do is you have |
|
| 79:33 | acceleration is equal for over the mass the force we've been working with the |
|
| 79:38 | . And so the acceleration is Given by the green of the stress |
|
| 79:46 | by the density. So the next is we write this out this acceleration |
|
| 79:56 | terms of the second derivative respect Right side is the same and this |
|
| 80:04 | the vector equation or motion with the explicit. However that's not what we |
|
| 80:10 | because uh what's the what's the unknown ? Is it displacement? Or is |
|
| 80:17 | stress? Uh The displacement is hidden the stress. And so that's what |
|
| 80:22 | gonna do is make it less uh hidden by using a hook slow. |
|
| 80:29 | here's what we had before. And put right in here uh Hook's |
|
| 80:34 | And this has got Stiffening the 4th Stiffness Matrix. And because this is |
|
| 80:45 | . J. Here, it's iJ and then Eminem here some of these |
|
| 80:51 | M. S. And ends. now we have um uh huh strain |
|
| 80:58 | the right and placement on the So we expressed the strain in terms |
|
| 81:06 | this. This is our definition of , small stream. And so |
|
| 81:13 | because of the symmetries inside here, can simplify things around. Uh You |
|
| 81:20 | uh all this later for yourself, it works out that this some cancels |
|
| 81:29 | this two. And left for this of this symmetry in the stiffness. |
|
| 81:39 | said. What we're gonna do then we're going to assume the medium is |
|
| 81:43 | . Take this C I. M. N. Outside here. |
|
| 81:47 | you will have, I noticed that trump in the earth. Uh there |
|
| 81:57 | various rock layers and so forth. so uh uniform the beating is not |
|
| 82:05 | in here. So I ask you bear with me for uh and give |
|
| 82:14 | a little slack here and we'll consider case first with the uniform medium and |
|
| 82:21 | we're gonna get to more realistic. this is however, not the wave |
|
| 82:29 | looks like it is because it's got these uh two respected time here to |
|
| 82:36 | respective space here, but it's not wave equation because this is not the |
|
| 82:42 | operator here. It's almost the way black part. We're not there |
|
| 82:53 | Okay, so there are various ways proceed from this point. Standard way |
|
| 83:05 | proceed. It was an argument due uh hair home loans. So we're |
|
| 83:17 | do that here. It's not my way. But uh let's do it |
|
| 83:27 | , because this is the standard way be frank. I don't know whether |
|
| 83:34 | not I spelled the name right? I think there's a T in |
|
| 83:45 | but I'm not sure anyway. He another one of these 19th century german |
|
| 83:51 | . And what he proved this which is described in the glossary uh |
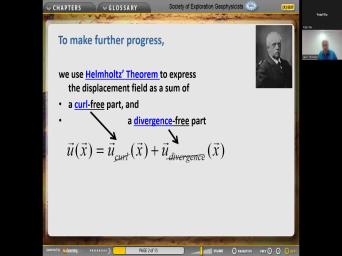
|
| 83:58 | um they're more shadows the following that any vector function of a vector |
|
| 84:08 | You can separate it into two One part has zero curl and the |
|
| 84:13 | part has zero divergence. But let's about what that means. As we |
|
| 84:22 | yesterday we found that um gradient of scalar As zero curl and you remember |
|
| 84:32 | the curl is an operation uh which you, which tells you the curly |
|
| 84:43 | in a in a vector field. here's a vector field here, it's |
|
| 84:48 | vector defined as uh in a field position vectors. And we can define |
|
| 84:58 | curl operation, it's complicated with and talking about yesterday and if we take |
|
| 85:04 | curl, This part of it here said to have zero curl. So |
|
| 85:12 | know from the work we did yesterday uh This part here with zero curl |
|
| 85:21 | be expressed as the gradient of a because we know that the gradient of |
|
| 85:27 | scalar has zero curl. So if operate on this thing, uh if |
|
| 85:43 | take the curl operation on this curl here, in curl operation here, |
|
| 85:47 | one goes away because it has zero and that's what it says here. |
|
| 85:54 | similarly, uh hum host guarantee, that the rest of this unknown displacement |
|
| 86:05 | gonna have zero divergence. So that that uh that we can write it |
|
| 86:11 | the curl of another quantity. We call the vector potential. So cy |
|
| 86:19 | sigh with little air order. That's the vector potential. This is a |
|
| 86:23 | potential. And we know that if take the virgin the divergence of this |
|
| 86:28 | , whole thing, we're going to the divergence of this, that's going |
|
| 86:31 | be non zero. But the divergence this is gonna be zero. The |
|
| 86:36 | of a curl of anything is So when we separated into these two |
|
| 86:42 | , we introduced these two ideas of scalar potential and effective. So this |
|
| 86:52 | what you find in the glacier. operator del can be applied to a |
|
| 87:00 | like this to make a scaler. can also be applied to a vector |
|
| 87:04 | make another vector. And that's the operation. And here is the definition |
|
| 87:11 | , definition of the divergence operator and definition of the curl. Yeah, |
|
| 87:23 | back to what helm whole said had of this thing can be described in |
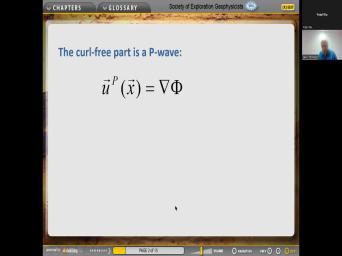
|
| 87:31 | of a scale of potential. So uh uh so let's concentrate on that |
|
| 87:36 | we're gonna call that because as we about the P wave as it's going |
|
| 87:43 | . It's uh not curly, it's of uh making uh dilatation and compression |
|
| 87:53 | dilatation. It's not doing this. intuitively, we think that uh curl |
|
| 88:00 | part is gonna be the P And so let's concentrate on that. |
|
| 88:05 | it's according to uh if we write this way in terms of a scalar |
|
| 88:10 | , we guarantee that it has no correspondingly the other part uh as a |
|
| 88:19 | waves. So as the shear wave growing along, it has none of |
|
| 88:23 | had no divergence. And so we write it as uh that's what we're |
|
| 88:29 | to call that. The shear wave , the solution has zero divergence. |
|
| 88:37 | , this separation of P waves and ways is uh doesn't work for anti |
|
| 88:45 | rocks. You can still help holds still correct. You can still separate |
|
| 88:52 | displacement into Pearl three part and divergence part. But those two parts are |
|
| 88:59 | P. And S. So we a different set of ideas to uh |
|
| 89:08 | uh P. And S. In psychotic rocks real walks. So uh |
|
| 89:17 | do that later. This is the way. It's good for tropic |
|
| 89:22 | Okay, so um uh what this is that um look for P wave |
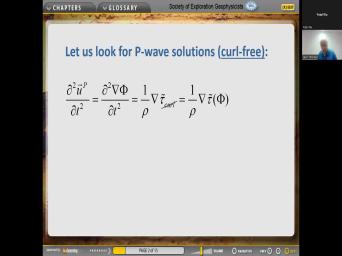
|
| 89:34 | by putting in here, the P is part of the displacement field and |
|
| 89:43 | gonna um left side is is We just put it in here. |
|
| 89:51 | uh reading of fun here, we it vague. We just said that |
|
| 90:00 | tao we're gonna take we already know gonna take the gradient of town gradient |
|
| 90:05 | stress, but now we say that stress is dependent only on this scale |
|
| 90:10 | potential five. So in the expectation looks like this and The single derivative |
|
| 90:18 | respect to J. But for all different Jay. Yeah. How is |
|
| 90:24 | going to depend upon the scale of . Okay, so in using hooks |
|
| 90:32 | , like we just did before, here's our stiffness matrix and here's our |
|
| 90:40 | and uh here's our strain right right here. And you see here were |
|
| 90:45 | that it's only the p wave part it here, we're talking about. |
|
| 91:02 | since this is a function only of , we can write it like this |
|
| 91:07 | uh simplify this expression and now it's close to uh something we can work |
|
| 91:20 | but actually it's uh I said it , it's not yet close because on |
|
| 91:26 | left side we have secondary time, what we want. But it also |
|
| 91:31 | um um uh gradient with respect to I skipped over. Where did that |
|
| 91:43 | from? Let us uh Let's back to here. This is uh the |
|
| 91:51 | of motion that we have and now gonna take the uh the gradient of |
|
| 92:02 | . Why did I do that? because uh this curl free part |
|
| 92:07 | uh displacement is the gradient of So that's just a simple substitution here |
|
| 92:17 | displacement. And um but in the of potential in here and also here |
|
| 92:23 | here. You see where it ends here. And so uh working down |
|
| 92:28 | the uh the algebra, uh it's complicated expression and particularly we've got three |
|
| 92:36 | with position down here and uh mixed over here. So we have some |
|
| 92:42 | to do already. You can see this is complicated, It's complicated. |
|
| 92:49 | way this is three equations. Reports I equals 1 to 3. And |
|
| 92:53 | you examine this all these sums sums , em sums over K and sums |
|
| 93:01 | J 27 terms in each of these . So what a mess, let's |
|
| 93:07 | examining one of the these equations, component is uh so we're gonna choose |
|
| 93:17 | equals three right here, here's the component and uh a few. That's |
|
| 93:24 | it looks like on the right I'm gonna go back here and just |
|
| 93:30 | into a three right here and it J K. And M J |
|
| 93:37 | So there they are. So let's the sum over J explicitly. So |
|
| 93:45 | is uh J. P is one really respect. Uh That's one. |
|
| 93:54 | and that's multiplying uh that's operating on here, which is the rest of |
|
| 94:02 | . So take this part of this , stick it over here and and |
|
| 94:08 | show the sum over J explicitly Now at this point we're going to |
|
| 94:18 | the tropic elasticity. So here's our matrix with zero's over here, zeroes |
|
| 94:31 | here and now we stick that into and uh extinct that into this |
|
| 94:39 | And because of all these zeros, lot of those terms disappear. And |
|
| 94:43 | only surviving terms are these here. still a lot but um Start off |
|
| 94:53 | 27 and 27 terms and were less one 1234567. Okay, so we |
|
| 95:04 | rid of 20 terms because of, assumed by Satrapi. So now let's |
|
| 95:11 | uh the two index work notation. , so right here, C |
|
| 95:17 | C 3131, sequel to C 44 so on. So now these equations |
|
| 95:25 | simpler and we're gonna collect terms uh , didn't we? We're gonna go |
|
| 95:46 | and do these uh summations. Once assume um linear, once we assume |
|
| 95:55 | psychotropic elasticity, we've got all these out here. And so we get |
|
| 95:59 | lot of zeros. But now these of over M and K are all |
|
| 96:04 | now. Uh and uh we're gonna those by recognizing that this one |
|
| 96:14 | These two are obviously the same Uh and it doesn't matter what's the |
|
| 96:19 | of Differentiation here, so that that shows up on the next page. |
|
| 96:26 | also we go from four uh index to and so this is beginning to |
|
| 96:33 | more simple. And now we're gonna terms and we find uh only these |
|
| 96:41 | terms that we have now sums of , ambulance and using the common |
|
| 96:51 | Now's a good time to change the names. So for example, this |
|
| 96:55 | 31, C 31 is uh and C. 44 is view And |
|
| 97:04 | . 3 3 M. And uh here that we have Also uh C32 |
|
| 97:15 | Lambda. And because of psychotropic and have two more here. So this |
|
| 97:21 | this some turns out to be the identically as this. Some and you |
|
| 97:26 | from the previous slide that these sums equal to M. And so all |
|
| 97:33 | terms are proportional. So we can out the M. And we get |
|
| 97:39 | the uh we get the little policy operator. So after all this uh |
|
| 97:47 | . We find for this vertically traveling , p way. Uh we find |
|
| 97:55 | simple wave equation like we have but instead of kor role here we |
|
| 98:00 | ammo and we can do the same for the other two components. And |
|
| 98:07 | we find the vector wave equation for waves looks like this. And uh |
|
| 98:13 | like we did in the ocean, can give this ratio a name, |
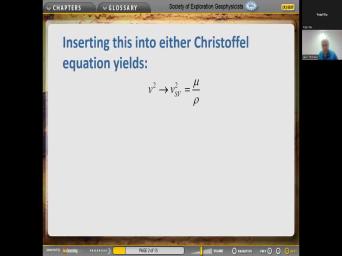
|
| 98:18 | gonna call it V. P squared remember all of this is about uh |
|
| 98:23 | wave from and you know from previous that aim is related to K and |
|
| 98:30 | in this way. And it's I it's better to give it a name |
|
| 98:34 | is launch launch funeral marshals because in way of inflation never find K appearing |
|
| 98:42 | itself only in this combination. You a name call again. So finally |
|
| 98:48 | get vector wave equation which looks a like the scalar wave equation except that |
|
| 98:57 | different. It has different um components the displacement in here and it's in |
|
| 99:03 | of displacement, not pressure. So like we did before, it's easy |
|
| 99:12 | convince yourself that all the solutions depend on the phase, here's a phase |
|
| 99:18 | in this three dimensional form, but the length of the wave vector is |
|
| 99:24 | in terms of the angular frequency and p wave velocity this way. And |
|
| 99:31 | you gotta remember that, this doesn't the various components of K. Only |
|
| 99:37 | length of stay. Yeah, this what we just uh derived. But |
|
| 99:50 | what we do is we can put say this is the gradient of the |
|
| 99:55 | the scale of potential, put it right here and put it in right |
|
| 100:03 | and then take these uh green operations here, like this one here and |
|
| 100:09 | one comes out here. And because the gradient operator is operating on the |
|
| 100:17 | thing, it comes down to the equation here, but see how this |
|
| 100:23 | is different from this one is this a scalar equation. This is where |
|
| 100:28 | is three equations in one vectors. is scalar wave equation. This is |
|
| 100:36 | scalar equation or p waves always in solid. It looks a lot like |
|
| 100:45 | scalar wave equation for uh waves in ocean. Remember in waves in the |
|
| 100:52 | there are no shear waves, there's uh p waves. So we didn't |
|
| 100:56 | to put on there. The subsequent remind us that it was the waves |
|
| 101:02 | because we know that in the the only sound waves travel the p |
|
| 101:06 | and we call the uh unknown uh we call the pressure or we call |
|
| 101:14 | dilatation. Otherwise this formula looks the . It's a scalar equation, not |
|
| 101:21 | vector equation. And the thing is we cannot measure fine, No way |
|
| 101:31 | us to measure uh this scalar But once we know there's a solution |
|
| 101:38 | like it's supposed we program our computers predict um synthetic science program in this |
|
| 101:51 | looking only for p waves. And we program it to make solutions for |
|
| 102:04 | from the scale of potential. So we end up with the answer in |
|
| 102:11 | computer, okay let's what can we to compare that with actual data? |
|
| 102:16 | we do not have any data for . But then we we can take |
|
| 102:22 | the gradient of the answer in the . The greeting of the solution. |
|
| 102:29 | that is gonna yield us um size with three components. You pete the |
|
| 102:39 | P vector. So why would we to do that? Well if we're |
|
| 102:44 | equations in the computer it's easier to a scalar equation than a vector |
|
| 102:49 | Right? Whatever numerical things you're you're doing it with a scaler instead |
|
| 102:54 | vector components. So it's easier to . Um Pewter should make it a |
|
| 103:03 | science program in terms of potential. then once you have the solution then |
|
| 103:10 | take you take the gradient of that in the here and that's gonna feel |
|
| 103:16 | acceleration for that uh synthetic seismic And then you can compare that. |
|
| 103:29 | , in a similar way, it's to show that if you work with |
|
| 103:35 | vector potential and the vector potential has equation like this for. and the |
|
| 103:43 | difference is there's two differences. Um this is the unknown as a vector |
|
| 103:50 | , not a scale of quality. the parameter of the material parameter is |
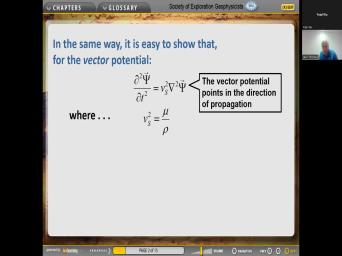
|
| 103:55 | shear wave velocity, p wave But otherwise it's the same. It's |
|
| 103:59 | two contributors we expected at the time it's got the little posse operator |
|
| 104:05 | And uh it's it has the same that you can you know, playing |
|
| 104:13 | from the this vector, what how is this vector related to the |
|
| 104:24 | real way? Remember this is a function, not not the displaced. |
|
| 104:31 | for a share way you have two involved, you have the direction of |
|
| 104:38 | of the share way and you also the direction of polarization. Sure. |
|
| 104:44 | . So uh which of those is anything um What is cy cy uh |
|
| 104:58 | gonna find the displacement function by taking curl, I'm sorry. And that's |
|
| 105:06 | give us the displacement of the Sure . And the uh the side victor |
|
| 105:17 | out points in that same direction of of the share wave did not point |
|
| 105:23 | the direction of polarization. So just with the P wave, it depends |
|
| 105:31 | on the face. But the face is is his faith. Is is |
|
| 105:37 | like this where it's related to the with the sheer velocity of the p |
|
| 105:47 | . So I want to know what in this place. Let me just |
|
| 105:50 | the curl of this equation. This us an equation affect your equation for |
|
| 105:57 | rates. This displacement is now perpendicular back here we decided that uh side |
|
| 106:16 | in the direction of propagation but the is sideways to that and it's perpendicular |
|
| 106:24 | the to the operation. So let's about think about the solutions to these |
|
| 106:40 | Mhm. With uh to these vector equations, the solutions have uh you |
|
| 106:50 | have the um represent, represent represent solution any problem as some of a |
|
| 107:01 | solutions like plane waves, plane waves often the best I could use um |
|
| 107:09 | solutions I think about the solution to problem as a sum of plane |
|
| 107:15 | And in that psalm there's it's a sum. There's lots of different uh |
|
| 107:22 | parameters And uh those are gonna be by the initial conditions in the brown |
|
| 107:30 | conditions. And I guarantee you that when we do all that we're gonna |
|
| 107:35 | real quantities on both sides of the . In all cases the solutions are |
|
| 107:44 | of the phase function which is defined this way where the length of the |
|
| 107:49 | vector is given for p waves like , your waist like this because someone |
|
| 107:57 | this is still a solution because these linear equations and waited some still a |
|
| 108:04 | . Yeah, let's have a little and then take a break Stephanie or |
|
| 108:20 | equation of motion is the starting point this derivation of of the venture wave |
|
| 108:30 | false. Okay. So where do think the the starting point is? |
|
| 108:55 | . Well we started off with Equals and uh we start off with |
|
| 109:00 | forces and then we we put them an equation F. Equals M. |
|
| 109:04 | . So that's the equation of And and the only difference is we |
|
| 109:07 | uh looking at all the vector components of the pressures. So the answer |
|
| 109:13 | this one is true. Okay, this true or false? Read |
|
| 109:30 | Yeah that one's true. It's just matter of properly accounting for all the |
|
| 109:36 | on the box. Remember that? got to read it carefully and think |
|
| 109:46 | it because there might be tricky for . That's correct. Very good for |
|
| 109:54 | . Very good. Yes sir. is I have to think about this |
|
| 110:12 | lot. So think out loud as thinking talk. Um Well I can't |
|
| 111:01 | d because you know what pressure, don't know what potential is. I |
|
| 111:05 | it's kind of a fuzzy idea Uh There's gotta be a difference. |
|
| 111:19 | Yeah, so let's talk through Let's start with a the so called |
|
| 111:24 | and a P wave in a silent really launch, you know, |
|
| 111:27 | Not corporate, Is that true or That stable? I'm gonna say that's |
|
| 111:35 | but uh that's not an answer to question. Okay so uh now uh |
|
| 111:43 | two is we program our computers to uh the equation for five for increased |
|
| 111:50 | because it's easier to calculate the scalar vector also true but not in answer |
|
| 111:55 | the question. Um I think you're . I think that the answer is |
|
| 112:03 | because the pressure P. Is the , whereas the potential fire is not |
|
| 112:08 | . Instead we can derive from by observable which is uh displaced. |
|
| 112:16 | So I like that analysis. Look the bottom number D. Is all |
|
| 112:24 | the box. So so you want go through these, talk your way |
|
| 112:28 | this and say does he could start a is that one true or |
|
| 112:47 | Okay that's good. So I'm not to be okay. Now here is |
|
| 112:59 | we got uh so we got two them are true. So we don't |
|
| 113:04 | to just assume that uh C. true. Uh and give and give |
|
| 113:11 | answer D. Because it might be . So let's analyze see as |
|
| 113:16 | is that true? The displacement field a shear wave has no divergence |
|
| 113:27 | This property of the way. And nous is this property. And so |
|
| 113:33 | the sheer way the displacement doesn't do at all. It only does this |
|
| 113:38 | it doesn't have any divergence. So true. Also so uh all of |
|
| 113:44 | above is um correct answer. Okay now uh this is a good place |
|
| 113:52 | break. And so uh let's do . Let's take a quick break and |
|
| 114:02 | back. Let's see um Let's come at 11:00. We'll resume at |
|
| 114:10 | Okay, So we resume the lesson a short break. And so what |
|
| 114:17 | just went through with the potentials and is the standard way of doing |
|
| 114:22 | But I was I've always been uncomfortable that myself because of these potentials. |
|
| 114:28 | me, a potential is sort of fuzzy concept. Uh And uh it |
|
| 114:33 | uh it's not observed, it's not . And uh we already said that |
|
| 114:40 | ahead is not gonna work for an tropic materials uh even though how most |
|
| 114:46 | still works, it doesn't uh the free part is not um it's not |
|
| 114:54 | P wave and uh diversity free part not sure. So let's look at |
|
| 115:02 | same issue um without potentials. So have this equation, here's the equation |
|
| 115:11 | the uh victor way field. And got all these complications and all these |
|
| 115:22 | over the various components. And notice that I uh instead of writing down |
|
| 115:29 | um uh for the component, we're really need to use that symbol I |
|
| 115:36 | it squirt or -1. So so this changed the name there of that |
|
| 115:46 | of that index. And so we to uh So this displacement could |
|
| 115:53 | you know, lots of different p in it from coming from all |
|
| 115:58 | And it could have share waves as . And so um let's think about |
|
| 116:05 | to separate that separate out those parts assuming potential function. No. Um |
|
| 116:18 | since we are two physicists, not , we're gonna solve this in the |
|
| 116:24 | rate. We're gonna guess the answer then we're gonna verify the guests. |
|
| 116:31 | , So we're gonna we're gonna recognize any solution can be expressed as a |
|
| 116:37 | year, a sum of plane So you recognize Stephanie, the plane |
|
| 116:42 | thing here, uh orders number with exponent I to the phase factor. |
|
| 116:49 | then out in front we have uh have a scaling factor awaiting function. |
|
| 116:57 | you see it's a vector just like full displacement is a vector. And |
|
| 117:06 | gonna sum up terms like this. the the important new idea on this |
|
| 117:13 | is I've used the term for So, um you are familiar with |
|
| 117:21 | your analysis of uh wiggles for and any time function. You're familiar |
|
| 117:30 | the fourier analysis of that time. uh and you can read more about |
|
| 117:36 | by the way in the blossom, look up for you. But there |
|
| 117:46 | will find, let me see here the glossary, you will find that |
|
| 117:53 | just like you can do for a a decomposition of a time series, |
|
| 117:58 | can do for a decomposition of a of position. And you can do |
|
| 118:07 | a decomposition of a vector function of and you can um do it |
|
| 118:16 | you can do a joint for your in time and space. And in |
|
| 118:22 | these cases. What fourier proved was uh East fourier components, which we |
|
| 118:33 | deduced using the recipe given by Fourier sufficient to describe anything. Any function |
|
| 118:43 | time and space can be represented as from as a sum of 40 |
|
| 118:49 | Like I just described whether uh and kind of puzzling because uh you know |
|
| 119:02 | any fourier component is a wiggle, co sign or a sign that goes |
|
| 119:08 | for about. How can we possibly a localized time signal which has a |
|
| 119:17 | point and an ending point? How we make uh that out of a |
|
| 119:22 | of um oh science and co signs goes on forever. And the answer |
|
| 119:31 | that you can do it and uh choose the uh the aptitudes in that |
|
| 119:42 | and that for you some assume you the the amplitudes of each ah of |
|
| 119:52 | term in a clever way. So reinforced together for short times and then |
|
| 119:58 | a long time they all cancel each out. So you get a localized |
|
| 120:03 | function and the same thing for a space function and the same thing for |
|
| 120:08 | time and space together Now. So call that a basis. Uh we |
|
| 120:15 | that the 48 basis. So uh these signs and co signs with uh |
|
| 120:21 | various uh frequencies and wavelength and so . Uh it's called a basis. |
|
| 120:29 | so So the reason I use that fourier right here is that those basis |
|
| 120:36 | are in fact plan weights. So these plan wave term that I'm showing |
|
| 120:41 | are exactly uh 48 uh basis functions we just talked about. And so |
|
| 120:48 | why it's so useful to talk about waves because although we never see in |
|
| 120:54 | mix, we never see a plane . We know that any solution can |
|
| 120:59 | expressed as a sum of plane wave those. Uh And that's true for |
|
| 121:07 | scalar function like a time series. true for uh for a vector uh |
|
| 121:14 | like uh display shin the J function the J component of dysplasia. And |
|
| 121:19 | it means is that the uh waiting terms are directors and we call these |
|
| 121:31 | that the collection of these uh waiting for the various four year terms. |
|
| 121:36 | called the spectrum. So here uh upper tissue gives the spectrum both in |
|
| 121:43 | and space uh for the collection of waves. So we're gonna make this |
|
| 121:52 | and then put that into um the of motion. And when we uh |
|
| 122:01 | we do that and make the two derivatives from the equation of motion on |
|
| 122:06 | left side, that brings out a omega squared. Why is that? |
|
| 122:11 | need to uh we need to talk that. Let us stop right |
|
| 122:18 | I'm gonna stop right here. Don't the recording. Um So what I'm |
|
| 122:23 | do is get out of this file I'm gonna open up lost three |
|
| 122:41 | Can you see that on zoom? . So I need to stop sharing |
|
| 122:49 | I have to re share. Okay now we're in the glossary. And |
|
| 123:02 | let's go down and find uh oilers . Here's oilers number. It's a |
|
| 123:19 | number named after Leonardo or lor and the special thing about uh oilers number |
|
| 123:28 | you have Oilers number and you raise to a Power. Uh And I'm |
|
| 123:34 | call it power as A. Times . And then take the X. |
|
| 123:37 | of it. What that means. that because of the special properties of |
|
| 123:43 | . That derivative looks like the original . Each of the K. |
|
| 123:48 | R. Now multiplying by K. , now um let's see here. |
|
| 123:57 | This is uh I don't know whether is gonna work. I'm gonna click |
|
| 124:03 | and see uh thanks see where it to take me. It wants to |
|
| 124:14 | me to Wikipedia. So in Wikipedia lots of information about oilers number. |
|
| 124:23 | And so I didn't wanna repeat that . But here's the expense of the |
|
| 124:28 | property. When you take the derivative either the K. X. You |
|
| 124:32 | K. Times either the K. . Okay so um uh Stephanie uh |
|
| 124:41 | . Is that new to you or ? Mhm. Okay. So uh |
|
| 124:49 | now remember that. And and uh e is the only number in the |
|
| 124:55 | which has this property, so that's uh it's named after its discoverer. |
|
| 125:02 | I guess it's a german guy uh and I'm not sure uh where this |
|
| 125:10 | was taken from, I think this is taken from Wikipedia. So uh |
|
| 125:20 | stop sharing this and go back to lecture and I'm gonna share the |
|
| 125:34 | share my screen again. Is that on zoom now? Okay, so |
|
| 125:49 | me put this into presentation mode. , so what we're gonna do now |
|
| 125:57 | uh use that special property of E the wave equation and in the wave |
|
| 126:04 | , you know, we're on the side, we're going to take two |
|
| 126:07 | with respect to time. So when take two derivatives of this, you |
|
| 126:11 | I two of uh this is a e upper case U is a constant |
|
| 126:17 | course. Uh and uh two derivatives you. Uh two tutors of |
|
| 126:25 | the I omega T with inspector T i omega squared squared, omega |
|
| 126:31 | which means minus one is I squared squared. So this on the left |
|
| 126:36 | the result of taking two derivatives of and on the right is to derivatives |
|
| 126:43 | respect to uh directions. Uh L case I'm gonna back up here. |
|
| 126:55 | we have we need to take uh disrespect to K and N. So |
|
| 127:10 | . Yes. Okay, so this a little bit of bad pedagogy for |
|
| 127:17 | . So let me back up And so we have here uh index |
|
| 127:23 | . Obviously we're gonna get confused with when we talk about the wave number |
|
| 127:31 | . The length of the wave vector . So I changed that K. |
|
| 127:37 | L. Right here without telling And I should have told you I |
|
| 127:45 | go back and fix that up. putting this gas into the wave equation |
|
| 127:54 | this and you see this is there's more derivatives here. All the uh |
|
| 127:59 | got taken out and we did the when we uh when we applied the |
|
| 128:08 | we got a minus omega squared here we got a minus K. |
|
| 128:12 | Times K. In here. And what what was left was the original |
|
| 128:18 | function which got canceled out on both . And so this is just an |
|
| 128:24 | . It's actually three equations, algebraic , node privilege anymore. And what |
|
| 128:29 | the unknowns in this equation? it's the uh it's the use so |
|
| 128:36 | you j here and then we're gonna U. M sum with this M |
|
| 128:43 | , 12 and three. So this called the crest awful equations. Another |
|
| 128:50 | think was Um Dutch. That's right , 19th Century Mathematical Physics. We're |
|
| 128:58 | head. I said so this is the equations of motions for a single |
|
| 129:03 | wave for a component. So then have this constraint between omega and |
|
| 129:12 | So we put that in. So gonna divide uh huh by both sides |
|
| 129:21 | by K square. And so on left case grave. Uh on the |
|
| 129:27 | side of omega spirit be right about period, it's gonna be philosophy square |
|
| 129:32 | on the right inside and see a making a ratio with these others. |
|
| 129:37 | you recognize already these uh fractions here give the direction of the wave called |
|
| 129:46 | cosine. So uh polarization, uh know, the displacement is driven by |
|
| 130:01 | uppercase uppercase use and the way the is going is the way the wave |
|
| 130:07 | propagating is hearing by these caves. now let's talk about what kind of |
|
| 130:15 | we can get. Well, the solution is just to assume that uh |
|
| 130:21 | . Is zero on both sides. uh that's that that solves the equation |
|
| 130:30 | matter what is V. But that's useless solution. We call it the |
|
| 130:35 | solution. And so we're gonna seek solutions which are only possible for discrete |
|
| 130:43 | of V. And as we can get uh find certain values of the |
|
| 130:48 | in terms like this Uh for which use or non-0. So let's work |
|
| 131:05 | out explicitly. This is three equations one. So let's write out the |
|
| 131:10 | uh equations separately. And um we're gonna assume my socks. So |
|
| 131:24 | when we do these sums here because so many zeros inside here. Uh |
|
| 131:31 | lot of terms cancel out. You this is some something over M and |
|
| 131:36 | and hell. So there's uh 27 included in here, but a lot |
|
| 131:44 | them are zero because we're going to my socks. And the only ones |
|
| 131:47 | are left are these three equations in here are the three different equations. |
|
| 131:53 | you see what we have here. is the equation for you one. |
|
| 131:57 | on the right hand side it's also you three. So here's the equation |
|
| 132:02 | you three. And on the right side it's also got you one. |
|
| 132:06 | these two terms are a couple of two equations are coupled together, but |
|
| 132:09 | middle equation is not see we got you two on both sides of this |
|
| 132:18 | . So, let's solve this one . This will be easier. So |
|
| 132:23 | the solution for a plane wave propagating at any angle which is polarized in |
|
| 132:28 | two directions. So what are the of, of uh propagation? Or |
|
| 132:35 | given by K. one divided by , and K. Three divided by |
|
| 132:42 | . Whatever you choose for these, are going that's going to determine the |
|
| 132:46 | . And uh so uh intuitively we that uh propagating at any angle in |
|
| 132:59 | 13 plans. So look, let's that the 13 plane is the plane |
|
| 133:03 | the screen so this is the one here, in the three direction |
|
| 133:07 | the two direction is out of the and and into the plane. So |
|
| 133:13 | if the wave is propagating in this , but it's polarized if if the |
|
| 133:19 | are moving out of the plane, must be a share wave. And |
|
| 133:23 | , it's what we call an H. Wave because it's polarized always |
|
| 133:27 | the two directions independent of the angle propagation here. So, you know |
|
| 133:36 | SV waves. Those are those are be polarized in this plane. But |
|
| 133:42 | this is a um solution for the the S. H. Way. |
|
| 133:51 | by definition the polarization is like, so here are the other two |
|
| 134:03 | So first we're gonna seek a Certainly polaroid solution. So we're uh |
|
| 134:10 | gonna seek a solution which has uh uh in the direction of you. |
|
| 134:19 | here is you. And so uh . One and K. Three um |
|
| 134:25 | the direction of polarization. Uh So and this is a unit vector for |
|
| 134:31 | you. Uh So let's assume that you is pointing in the same direction |
|
| 134:40 | the wave. So that means that you is gonna have a vector |
|
| 134:46 | uh K. One over K. then uh component in the three direction |
|
| 134:53 | three over K. And so we put that assumption into here, it |
|
| 135:01 | matter which one we uh put in we uh use the velocity, which |
|
| 135:07 | showing right here that is given by . O. Ro And so we're |
|
| 135:12 | to call that the p wave And so our assumption of Washington polarization |
|
| 135:21 | produce um away traveling in the uh the same direction as the polarization, |
|
| 135:29 | direction as the displacement with this And so we call that the, |
|
| 135:37 | our guests for p ways. Now seek a transverse fully polarized. In |
|
| 135:42 | words, one uh we arranged the . Three and the K. One |
|
| 135:47 | this. This vector of uh unit displacement is gonna be perpendicular to the |
|
| 135:55 | of propagation. And why did we this? Well, we choose this |
|
| 135:59 | uh this dot product between you and . Zero if we choose you to |
|
| 136:08 | like that. And so if the product of U. And K. |
|
| 136:13 | , then those two vectors are perpendicular each other. So we're now going |
|
| 136:17 | find a solution where um where the to the obligation. And we insert |
|
| 136:34 | in decoration. And we deduce you follow this through on yourself when you |
|
| 136:39 | the V. Square is uh mu which we're going to call the sheer |
|
| 136:47 | for an S. V. Wave in the same plane. But a |
|
| 136:54 | wave also polarized polarized in the polarized perpendicular to the propagation at at |
|
| 137:02 | points. And it happens to have same shear velocity as the S. |
|
| 137:07 | wave. We didn't know that when started out, but now we deduced |
|
| 137:12 | that's true SV waves and S. waves have the same velocity for extra |
|
| 137:18 | media. And the only difference. The only difference is how those two |
|
| 137:26 | interact with a boundary. So when talk about reflections in next week we |
|
| 137:33 | find out that S. H. reflect differently than sp waves. But |
|
| 137:38 | that's a boundary. That's an issue arises when we have boundaries here. |
|
| 137:44 | haven't mentioned any boundaries or inside of body. And we have an SV |
|
| 137:48 | propagating this direction and S. Waves . Uh Both the SV waves and |
|
| 137:57 | S. H. Waves are propagating this plane, the end of the |
|
| 138:02 | , but the S. H. were polarized perpendicular out of the plane |
|
| 138:07 | the S. P waves are always the plane. So we confirm that |
|
| 138:12 | are um assumption of transverse polarization is . And we found the sp way |
|
| 138:26 | topic. So for as your tropic , we offer this call them S |
|
| 138:33 | an ice tropic bodies that's not going be right for an ice tropic |
|
| 138:38 | It's gonna turn out the same process to two different share wave velocities. |
|
| 138:45 | two different share waves. Two different waves propagating with different velocities in general |
|
| 138:55 | anti psychotropic bodies. And we're gonna the same process, use that um |
|
| 139:05 | a couple of years time. So found separately p waves and share waves |
|
| 139:12 | using potential function. And to me a much better way to think about |
|
| 139:19 | . I've always found potential functions to sort of a vague fuzzy concept. |
|
| 139:29 | call this a degenerate situation when we two different to uh to share waves |
|
| 139:35 | are completely different uh polarized in uh different directions at the same velocity. |
|
| 139:42 | call that a degenerate situation. But we have anisotropy that generously disappears and |
|
| 139:49 | have two different share velocities, Those uh properties for those two waves. |
|
| 139:55 | think about this, I'm gonna go um go back to this and uh |
|
| 140:05 | that gives me a clean screen. I have share waves traveling in this |
|
| 140:10 | with uh polarization in the plane. previously we found share waves traveling also |
|
| 140:18 | this, in this direction or any direction. Let's concentrate on this |
|
| 140:23 | Um with polarization pictures out of the also traveling with the same velocity. |
|
| 140:31 | what does that mean if you have you have uh shear wave traveling with |
|
| 140:39 | polarization which is neither in the plane perpendicular to the plane, but at |
|
| 140:44 | angle to the plane? Well, can be broken down into components parallel |
|
| 140:49 | perpendicular. They both travel with the velocity. So that one that one |
|
| 140:54 | which we just hypothesized with some random perpendicular to the propagation, but a |
|
| 141:01 | polarization in that plan, perpendicular that also works also in ice economic |
|
| 141:10 | . So the polarization can be uh in the perpendicular plane for ice comic |
|
| 141:18 | , but in anti ship topic that's not true. Only those two |
|
| 141:25 | directions that we just found uh work an ice traffic media and for an |
|
| 141:31 | traffic media. Uh If you try I don't know, I have a |
|
| 141:39 | wave with an intermediate polarization, it itself into so much of the uh |
|
| 141:46 | SV wave and so much of the . H. Waves. And those |
|
| 141:51 | each with their own velocity and so get one gets ahead of the |
|
| 141:56 | And so um that's just an example how in real rocks which are an |
|
| 142:02 | topic, everything is different for share . Okay, now let's think about |
|
| 142:16 | a homogeneous wave equation in homogeneous wave . So uh start with the vector |
|
| 142:27 | equations for p waves as we And so I moved the both terms |
|
| 142:37 | the left side of the equation. you will notice that in all terms |
|
| 142:41 | the all the non-0 terms here. unknown appears. And so that's called |
|
| 142:47 | that's called a homogeneous equation homogeneous Now we're gonna put another term on |
|
| 142:58 | right hand side which doesn't have the in it. So that's gonna make |
|
| 143:05 | in homogeneous equation. That's what I said right there. Now we're gonna |
|
| 143:11 | a point source at the origin reading in all directions. And so the |
|
| 143:18 | wave equation comes like this. And here we have um the chronic consumer |
|
| 143:32 | we have the direct delta function Which zero for all Radius R. except |
|
| 143:43 | Article zero. And it's radiating with vector wave which is uh could have |
|
| 143:51 | P waves. No, it's only have P waves in it because we're |
|
| 143:56 | here with p ways. Uh It's um have a time function which the |
|
| 144:03 | decides if he if he used that's one time function, but he |
|
| 144:11 | want to do something else. For , here's an example um um In |
|
| 144:22 | land acquisition for p waves, we don't use dynamite anymore. We normally |
|
| 144:30 | vibrators. So the vibrators are not to be uh expressions like this which |
|
| 144:37 | radiating uh where the uh space function equal in all directions. A vibrator |
|
| 144:44 | going to be focusing its energy So that kind of source is not |
|
| 144:50 | here. This is this is a source where it's radiating equally in all |
|
| 144:56 | . For example. Um If you an air gun in the marine |
|
| 145:02 | we can still use this vector wave in the marine environment. All we |
|
| 145:07 | to do is we set a new zero and suddenly presto change o the |
|
| 145:14 | wave velocity becomes uh the square of care of the world. So this |
|
| 145:20 | this expression is also going to be in the ocean. In the ocean |
|
| 145:25 | typical sources are air guns. And the air gun uh emits um oh |
|
| 145:36 | of compressed air into the water. the pulse expands, bubble expands and |
|
| 145:43 | it over expands and then it like, so it has various false |
|
| 145:50 | of the bubble. So that makes extended time series like this uh that |
|
| 145:58 | out spherical waves through the water in directions, the same in all |
|
| 146:03 | Um but it has a complicated time . So that's why I've left |
|
| 146:08 | This time function to be uh not , but I did specify here that |
|
| 146:15 | gonna be radiating equally in all Just for simplicity. Uh the solutions |
|
| 146:23 | uh vibrator are more complicated, not to be handled in this court. |
|
| 146:33 | will know uh Previously we we ignored term. We just said what happens |
|
| 146:43 | as a wave comes along and hits Vauxhall? What does the Fox will |
|
| 146:48 | with it? Well, the Vauxhall it along according to the material properties |
|
| 146:53 | the box. Uh but now we're , where did this wave come |
|
| 146:58 | Well, it came from the origin with this set of uh time various |
|
| 147:07 | to the source. Now notice here the unknown does not appear on the |
|
| 147:13 | hand side. So the mathematicians call this an in homogeneous wave equation. |
|
| 147:21 | a vector wave equation. And it's p waves because we said it's for |
|
| 147:24 | waves right here. So we're going find the solution in the next election |
|
| 147:30 | now. Uh I know that because origin at r equals zero is a |
|
| 147:40 | place. It's obviously better to use place um operator in spherical coordinates without |
|
| 147:46 | variation, which is given by So psi right, right here we |
|
| 147:50 | the place an operator and we could that in terms of Cartesian coordinates, |
|
| 147:55 | we would get into difficulties because here have the radius here. So we're |
|
| 148:00 | use the uh operator in spherical coordinates is here and right here, you |
|
| 148:09 | immediately see that at the origin where equal zero. That's gonna make a |
|
| 148:13 | because we're dividing by zero squared Also we're multiplying by zero squared over |
|
| 148:20 | . So things are gonna work it's it's not gonna be a |
|
| 148:25 | But we are gonna have to do little bit of work to express. |
|
| 148:30 | Yeah. You know, with that , when we have a source. |
|
| 148:40 | , so is this question for false homogeneous wave equation is the same as |
|
| 148:48 | derived earlier. Except that it applies non home genius, layered subsurface formations |
|
| 148:55 | true or false? That's false. . Right here, right here we |
|
| 149:01 | uh that it's because of the form the equation equation does not have the |
|
| 149:07 | on the right hand side. So what makes it in homogeneous equation. |
|
| 149:12 | the if the if the medium is homogeneous, that's gonna affect uh This |
|
| 149:19 | the material properties are given here. is the wave, this is the |
|
| 149:24 | right here, and this is the . The materialist is crashed here so |
|
| 149:30 | this statement is false. Yeah, are false. Is it the same |
|
| 149:36 | we derived earlier, except that it an extra term describing the source of |
|
| 149:40 | wave. That's true. Okay, now, now we're gonna do the |
|
| 149:48 | closer to the real Earth. Now nine uniform wave equation. Now here |
|
| 149:54 | where we previously assumed uniformity. Back page 63, we were working through |
|
| 150:00 | algebra and we wanted to take this , the stiffness tensor element out of |
|
| 150:07 | derivative. So we just assumed that doesn't vary with X. So we |
|
| 150:12 | put it out here and then we left with this and we eventually turned |
|
| 150:17 | into the wave equation, and actually separate wave equation for P N for |
|
| 150:24 | . So, now, what we to do is consider what happens if |
|
| 150:27 | don't do that. So, using chain rule calculus, we we find |
|
| 150:32 | this same right hand term has two to it. One which describes the |
|
| 150:41 | of this part, that's this, one which describes the variation of this |
|
| 150:46 | , which is this And so here have the gradient respected J. Of |
|
| 150:52 | stiffness element here. Right here, it's assumed to depend upon it. |
|
| 150:59 | the gradient is given right here. previously we assume this term is |
|
| 151:06 | but in the Earth, you that's not zero. So what are |
|
| 151:11 | gonna do about that you term, expresses the non uniformity of meeting. |
|
| 151:21 | , now, so let's suppose now have a layered me and suppose the |
|
| 151:29 | are this thick, we've got another down here, another just uh in |
|
| 151:35 | layers that pick down, suppose I'm ask you, Stephanie, uh are |
|
| 151:46 | gonna need this additional term here for short waves? The wavelength is only |
|
| 151:53 | long and we got a sedimentary layer is uniform within itself. We've got |
|
| 152:00 | wave run through there. Are we need this term here? Yeah, |
|
| 152:08 | right. We're gonna not gonna need for terms like that for terms like |
|
| 152:13 | or for ways like that, this going to go through the media. |
|
| 152:18 | I'm gonna use, my other I'm gonna go through the media thinks |
|
| 152:20 | coming up and it doesn't know about boundary, it doesn't know about the |
|
| 152:25 | until it gets this boundary. And then some of it's gonna reflect someone's |
|
| 152:30 | uh transmit. So that will be boundary problem. We'll talk about |
|
| 152:38 | get reflections and transmissions. But before gets there, it's propagating happily inside |
|
| 152:44 | inside the layer and it doesn't know eventually it's gonna hit a boundary, |
|
| 152:51 | just propagating. And so we don't this term and we can get away |
|
| 152:55 | neglecting it just like we've been neglected suppose that the wavelength is really long |
|
| 153:00 | the wavelength goes from uh the ceiling the floor and it's going through a |
|
| 153:05 | of layers like this. That's gonna a problem. That means we're gonna |
|
| 153:10 | terms like this to describe that And that's the real problem that we |
|
| 153:16 | have in uh in the earth where almost all seismology, we have uh |
|
| 153:26 | which are long compared to the scale of the in home of genetics. |
|
| 153:34 | that's gonna be a problem which we're have to deal with. But |
|
| 153:42 | And the reason we know that is could be in homogeneity on all |
|
| 153:49 | Let me see how we're doing with . Okay, we're doing fine. |
|
| 153:54 | this is a special kind of log is called a more whole image. |
|
| 153:59 | so this is a tool which is inside of a more whole and makes |
|
| 154:07 | uh um uh It acquires data as pulled up through the bar home. |
|
| 154:15 | as it pulled off its spinning rapidly spinning maybe uh Um 100 times a |
|
| 154:25 | or 50 times a second. It's really fast. And meanwhile it's being |
|
| 154:29 | up slowly as it's spinning around. emits high frequency sound uh into the |
|
| 154:37 | fluid, right? Uh You understand the borehole is normally gonna be filled |
|
| 154:44 | borehole mud. Why has it got in there? Well, uh it's |
|
| 154:51 | uh outside the bar hall there might uh fluids in the formation outside the |
|
| 155:00 | hall probably bright, maybe oil, gas, but fluids and they're going |
|
| 155:06 | be under high pressure. We don't those fluids to come into the |
|
| 155:10 | Oh, so there's two ways to that problem. One is to put |
|
| 155:15 | casing on the bar hall. But we do that, we want to |
|
| 155:21 | more about those formations before we hide with the cases. So we send |
|
| 155:26 | tool down, it's called a borehole tool and it's coming up and it's |
|
| 155:32 | in order to keep the fluids from formation out of the borehole, we've |
|
| 155:38 | to have mud in the bar hall enough density to make enough pressure in |
|
| 155:44 | borehole mud so that it's more pressure the mud than in the borehole |
|
| 155:52 | So we don't wanna have it uh don't want to have the mud too |
|
| 155:58 | because if it's too heavy then it's be leaking into the formation. We |
|
| 156:03 | to make it just a little bit . It's the pressure is just a |
|
| 156:08 | bit higher than the formation pressure even it's gonna leak out a bit. |
|
| 156:14 | the way it works is that as leaks out into the forest formation, |
|
| 156:18 | pores screen the mud particles out of mud and it leaves what they call |
|
| 156:25 | mud cake on the um On the of the uh four hole. And |
|
| 156:35 | mud cake uh is actually a good . It uh it decreases the |
|
| 156:41 | it clogs up the pores and decreases permeability in that mud cake so that |
|
| 156:50 | the mud particles stopped flowing out because get something clogged up. Okay? |
|
| 156:55 | it's only occupying the pore space only have to find the four space. |
|
| 157:02 | now this this uh that's why we mud. And so this tool is |
|
| 157:09 | pulled up up the bar whole spinning emitting high frequency sound. And |
|
| 157:15 | and the high frequency sound goes out the mud reflects off the bar hall |
|
| 157:19 | comes back to the instrument. It a receiver directly located at the |
|
| 157:26 | so the the offset between source and zero. And so then it records |
|
| 157:32 | amplitude of the sound which is coming . And so the amplitude of the |
|
| 157:37 | obviously depends upon the kind of rock is in the more whole wall. |
|
| 157:44 | , so now as it's being pulled , you can see that the different |
|
| 157:48 | here give the different amplitudes of reflection the reflection sounds. So they are |
|
| 157:57 | as it's being pulled up there showing different mythology. And so you can |
|
| 158:03 | the layers here. Now it spins and this display is unwrapped. So |
|
| 158:08 | goes from 0 to 360°. And so for some angles there's uh parts of |
|
| 158:16 | tool or in the way. So white lanes here, that means no |
|
| 158:19 | in that as a medical direction. as it's being pulled up, the |
|
| 158:25 | tool rotates slowly as it's being pulled . So that's why these asthma's are |
|
| 158:29 | straight up death. But you can see the layering on this scale. |
|
| 158:37 | 20 m showing here and now. let's zoom in zoom in here. |
|
| 158:44 | , you see more layering, Let's in again, more Larry, more |
|
| 158:48 | . This is zooming in uh 10,000 and on all scales blaring. |
|
| 158:57 | maybe this is not true for all for all sequences, but it's extremely |
|
| 159:02 | that you never have this situation where have a locally uniform, we'll always |
|
| 159:11 | that's true. So we neglect that homogeneous term. But so we pretend |
|
| 159:18 | it's homogeneous on the small scale and only have to worry about it at |
|
| 159:22 | risk at this layer boundaries. this says that there's a layer boundary |
|
| 159:28 | , no matter where you're looking. this this is a problem that we |
|
| 159:32 | to deal with. Uh we're not to deal with it. Now, |
|
| 159:36 | gonna deal with it later in the . This is exactly the kind of |
|
| 159:39 | world problem that most courses like uh ignore, but we respect your |
|
| 159:47 | and we uh we know that you've been out of school for a couple |
|
| 159:53 | years. You've been working is you some knowledge of the of the real |
|
| 159:59 | and you know that when I it's homogeneous uh layer like that? |
|
| 160:05 | probably nonsense. Yeah. Yeah. you take a tube sample and uh |
|
| 160:16 | how did how did you collect those samples by the way? Just a |
|
| 160:26 | of. Okay. Yeah. So normally these are fairly shallow. |
|
| 160:39 | Okay. And so the way they it, do you know how they |
|
| 160:43 | it in the field? Yeah. . So I think I know and |
|
| 160:51 | my company made a big um advance this years ago. So what we |
|
| 160:58 | was um uh well I'll suspend this I'll tell you this story because it's |
|
| 161:05 | kind of an interesting story. I at Amoco's Research Center and a lot |
|
| 161:12 | high quality people there and we had geophysics division and geology division and drilling |
|
| 161:19 | and so on and a computing And uh one of the senior guys |
|
| 161:28 | the drilling division had a bright he said you know these silly geophysicists |
|
| 161:35 | around with all their silly uh vibrators services and receivers and everything. Get |
|
| 161:42 | this data and do all those silly and they still don't know where to |
|
| 161:46 | the arm. Why don't we find by drilling? So this is an |
|
| 161:53 | that comes naturally to a griller. There's two answers to that. Uh |
|
| 161:59 | is drilling is too expensive. We just drill random. Uh But what |
|
| 162:05 | could do is we could say well don't we just uh drill in places |
|
| 162:11 | it's likely? And it's and the to that is it's still too |
|
| 162:15 | And so why is it too It's because we drill every hole with |
|
| 162:21 | expectation that we're gonna find oil in . And so the whole that we |
|
| 162:25 | is sufficient size to produce that Why don't we drill our holes in |
|
| 162:33 | different way, Looking for information, for uh not prepared to produce. |
|
| 162:41 | if if we drill the hole for only, it could be a lot |
|
| 162:47 | . Now, you know that if gonna drill down 10,000 ft, what |
|
| 162:51 | do is we start off with a which is maybe 30" in diameter. |
|
| 162:56 | as we go deeper, the the whole gets smaller, we line the |
|
| 163:04 | uh stretches of the hole with steel to keep the fluids out, formation |
|
| 163:13 | out. And then we drill deeper a pipe of smaller diamonds, we |
|
| 163:18 | the smaller diamond down through the big pipe. And so and so the |
|
| 163:23 | gets smaller as it goes deeper and that steel, and then big, |
|
| 163:32 | drilling rig. And so that's what the expense. So we could downsize |
|
| 163:37 | whole thing, Looking only for It could be a lot cheaper. |
|
| 163:44 | we invented at Amoco and then a where we could uh drill a hole |
|
| 163:50 | off with 4" diameter And ending up 10,000 ft 1" time. And the |
|
| 163:59 | we did it was we had a , a 40, a 40 ft |
|
| 164:06 | , just a simple pipe with industrial on the bottom on the pipe. |
|
| 164:11 | we spun that pipe in the hole then every 40 ft we would extract |
|
| 164:18 | easily, bend it and uh extract core, 40 ft long core all |
|
| 164:25 | way to the surface and then uh out the pipe and send it back |
|
| 164:30 | . And uh then eventually we'd have start decreasing diameter. But the whole |
|
| 164:38 | is a lot smaller and you see uh it chewed out um only the |
|
| 164:46 | . Whereas uh standard drilling choose out whole selling. So we should not |
|
| 164:53 | be honest and we uh accumulate all 40 ft course. So the first |
|
| 164:58 | they did this and by the way was done uh very high tech, |
|
| 165:04 | all the results uh monitored by computers I think tele meter back to our |
|
| 165:13 | in Tulsa in real time. Best in the world were monitoring this. |
|
| 165:18 | the bells and whistles. You can . Then after a while somebody noticed |
|
| 165:23 | the rig, of course the rig a small rig, not a big |
|
| 165:27 | , somebody noticed. Hey, look all these 44 cores here. I |
|
| 165:32 | if the geologists might be interested in at these cores. So, since |
|
| 165:37 | were drillers, they had no concept other people could contribute to the |
|
| 165:43 | So they said, well, and course the geologist said of course we're |
|
| 165:47 | . So they put together a a portable geological analysis laugh that they |
|
| 165:55 | bring onto the well site and look these four different courts. And also |
|
| 166:00 | was in the also that they asked uh you'd be interested in looking at |
|
| 166:07 | these parts. Well of course what do is we'll take uh subsections of |
|
| 166:13 | cards and measure the losses, and density and everything else we can |
|
| 166:18 | of. So we made an affordable to go to the well site and |
|
| 166:23 | measurements. So it was quite a system and we drilled maybe five holes |
|
| 166:30 | this, all of them successful. if you solve the pressure of uh |
|
| 166:38 | pressure, mhm. Even solve the . Um What would happen if we |
|
| 166:48 | into overpressure formations? Didn't have any measures for then against the possibility that |
|
| 166:59 | pressure fluids from below can come up this annual list and uh wipe out |
|
| 167:06 | crew. So uh the middle of we were solving that problem, BP |
|
| 167:13 | us and they threw away the whole . So it was not, they |
|
| 167:22 | made a good contribution but it was it was really interesting for us. |
|
| 167:33 | early stages and then we did a thing. We um we took our |
|
| 167:40 | laboratory to London and we put it the parking lot in the head office |
|
| 167:46 | London. He invited all the other companies operating in the North Sea, |
|
| 167:52 | was frontier area in North Bring us samples and we will we will give |
|
| 167:58 | a real sonic log made uh made of vertical while they couldn't do |
|
| 168:03 | See we we could sample every every if we wanted. We could we |
|
| 168:08 | sample every 10 ft. But we to uh every other operator in the |
|
| 168:14 | Sea bringing your conventional course and we'll for measure them for you cheaper than |
|
| 168:21 | and do it collapse offers this We did it for half price. |
|
| 168:28 | piste off core labs but got got lot of business other companies bringing us |
|
| 168:34 | course and we made it basically uh made no profit all for that. |
|
| 168:41 | we did. What we did do we got a complete database all that |
|
| 168:47 | from all over the North Sea. uh just like google is saving your |
|
| 168:54 | whenever you use google. We saved information to good permission. And so |
|
| 169:00 | we accumulate a very extensive database of measured uh from cores. Oh ah |
|
| 169:18 | look very efficient set up uh in efficient lab, it was the best |
|
| 169:26 | physics lab work. That purpose. the interesting thing that I found you |
|
| 169:41 | core out of this kind of rock shells sequence like it's filled with navy |
|
| 169:51 | and it's filled with foods which are high pressure in situ. And then |
|
| 169:57 | you pull it out, the fluids out. We got those of course |
|
| 170:06 | under high pressure within half an hour they came out and measure the |
|
| 170:12 | Then we set the samples on the , come back a month later and |
|
| 170:16 | them again. Guess what they had because it had dried out and made |
|
| 170:23 | changes once when we drive after it dried out and tried to re saturate |
|
| 170:28 | . Uh press it again to the pressures dollars because of uh on elastic |
|
| 170:44 | of permanent effects caused by uh drying of the sample just as it sat |
|
| 170:52 | on the shelf. And so what concluded was that every sample that had |
|
| 170:56 | ever previously been measured was wrong because didn't have it had in it the |
|
| 171:02 | of of desiccation from sitting on the for being transported from wherever it |
|
| 171:09 | Nobody had ever measured a fresh sample we had. And so what this |
|
| 171:16 | that every core measurement that had ever made was wrong for that reason may |
|
| 171:22 | a little bit wrong. Maybe a wrong, depending on pathology and the |
|
| 171:25 | they handled. So naturally core labs not very happy with this. That |
|
| 171:33 | the major finding. Anyway, of we verified that we have um Larry |
|
| 171:39 | homogeneous on all um on all So uh let's now think about what |
|
| 171:49 | that, what is that going to for us when we ignore that in |
|
| 171:54 | in our in our equations. So consider a simple case with laying |
|
| 172:01 | So that means that the derivatives in two directions, horizontal directions are zero |
|
| 172:06 | let's consider only vertically traveling P ways that U. One is zero and |
|
| 172:11 | 20. So we're only going to at this equation for you three. |
|
| 172:15 | this is the wave equation term that familiar with now and this is the |
|
| 172:19 | term and it's got in here uh with respect to a vertical position Z |
|
| 172:30 | the launch channel modular. So the is in here uh and variation of |
|
| 172:36 | modular is showing explicitly here and notice this has only a single derivative whereas |
|
| 172:41 | has two deliveries. Okay, so gonna be a problem. Um we're |
|
| 172:50 | gonna solve that problem today. Just it to your attention and I give |
|
| 172:55 | here a little quiz. This that's . So this is very similar to |
|
| 173:03 | question I asked you earlier with only few differences. Yeah, yeah, |
|
| 173:20 | this one is true. Okay, you will come back to that real |
|
| 173:29 | issue later in the course. So let's talk about solutions to this. |
|
| 173:39 | , so this is uh solution. is a a nice graph taken from |
|
| 173:45 | and guild art which I recommend that should buy and um uh it shows |
|
| 173:52 | a function of arrival time here and a number of different lines of uh |
|
| 174:00 | . And so let's uh let's look the first one here is the direct |
|
| 174:05 | which is going from the source at to uh to uh all these different |
|
| 174:12 | . And it's a straight line which that the velocity is um a |
|
| 174:17 | And it's and uh we're measuring in surface of course. And of course |
|
| 174:21 | source the sources of the surface. it's uh propagating horizontally And in this |
|
| 174:29 | it has a velocity of about 650 . That's what they assume in |
|
| 174:38 | And of course they calculated this with model. Now look at branches, |
|
| 174:47 | . And C. Here here is . B. And here is seen |
|
| 174:53 | these are refraction. So you don't yet what a refraction is but I |
|
| 174:58 | tell you that a refraction is where body wave, like we've been talking |
|
| 175:05 | , body is inside the body of hits a boundary at a highly oblique |
|
| 175:12 | and some of it reflects and some the uh refracts. And uh uh |
|
| 175:20 | me say uh differently, some of reflects and some of it transmits and |
|
| 175:28 | amount of reflection and the amount of varies as function incident. So for |
|
| 175:34 | incidence angles that transmitted uh transmitter wave also as a parallel to the boundary |
|
| 175:43 | going horizontal. And that's what we're what we call refraction is here and |
|
| 175:48 | travels with the velocity of the lower . And so here you have to |
|
| 175:55 | layers. And uh B. And . Now look at look at |
|
| 176:02 | see it's a straight line uh far , trace it back closer to neuroscience |
|
| 176:11 | you see it merges tangentially with this reflection which is going to come up |
|
| 176:17 | a second. So this point here uh where uh one obtain agency that |
|
| 176:25 | occurring at an offset. Such that the uh um that offset the incident |
|
| 176:37 | um starts generating two waves, reflected and a and a refracted transmitted |
|
| 176:46 | And that one comes uh he didn't a good enough um description of that |
|
| 176:54 | . So uh what it does is comes down to the boundary at large |
|
| 177:01 | . The transmitted wave is parallel to boundary. And as it goes parallel |
|
| 177:05 | greedy energy upwards every point along And that's what we're that's what we're |
|
| 177:12 | here at the surface. We'll talk about that when we talk about reflections |
|
| 177:17 | transmissions because that happens because of the . So so these are two different |
|
| 177:23 | with uh two different layer boundaries given these two different uh velocities below the |
|
| 177:32 | . And then here are some And these are the ones who were |
|
| 177:36 | interested in E. F. And d. 1st d. Sorry here's |
|
| 177:46 | , here's the writing. So this uh is coming off the same layer |
|
| 177:53 | this. Refraction. They didn't uh didn't Mhm. Show any reflection. |
|
| 178:05 | refraction here. Show one here. show one here, I guess. |
|
| 178:13 | that's because of the properties of the and these are the ones that we're |
|
| 178:18 | interested in. And you will of uh recognized these uh hyperbolic move out |
|
| 178:29 | for E. And for E. F. And what we're measuring here |
|
| 178:36 | the move out velocity for that reflected . So here is a a a |
|
| 178:46 | from a reflection. And uh let's here. How do I know it's |
|
| 178:53 | a from a dipping p reflection. because it's a hyperbole to but the |
|
| 178:59 | the earliest arrival time is not The earliest arrival time is over |
|
| 179:04 | These offsets. So that what that is dipping and furthermore, look |
|
| 179:11 | here is a here's a hyperbole. might have thought that's a reflection. |
|
| 179:15 | here it's identified as a multiple. I think that that wave has gone |
|
| 179:22 | the source down to this reflector back to the surface and then back down |
|
| 179:29 | and uh is recorded at this So that's multiple when it has uh |
|
| 179:37 | reflections. And then we got more here off different reflector. And then |
|
| 179:43 | addition these these are here are called surface ways Sheriff and Gil lark called |
|
| 179:55 | . Ground roll. That's the old uh term my father's generation for surface |
|
| 180:03 | . And the airwave is K. So so here's the ground roll and |
|
| 180:11 | . And the air waving K. you see these are straight lines back |
|
| 180:15 | the surface. Uh And you see um uh they are a little bit |
|
| 180:29 | than the direct way. So the was traveling with a P way p |
|
| 180:33 | . This is slower, this is surface wave velocity. And this is |
|
| 180:38 | yet. This is traveling through the . So um uh Stephanie, have |
|
| 180:44 | ever been on a seismic acquisition Have you ever been on a seismic |
|
| 180:54 | group? And what what were they for Sources Viber side? So when |
|
| 181:02 | virus size was operating, you could in your shoes, you're standing some |
|
| 181:07 | away. You could feel the direct of arriving and you could feel the |
|
| 181:11 | roll arriving. Uh You probably couldn't here an airwave couldn't hear it in |
|
| 181:17 | ears, could you? Yeah. engineering. If they had been |
|
| 181:25 | then you would you would have heard dynamite blast in your ears. |
|
| 181:32 | And then we have the fractions which haven't talked about yet. So we |
|
| 181:38 | talk uh later about um oh. . Refraction and diffraction and reflections and |
|
| 181:50 | . Each of these lines represents an time. It's an arrival time for |
|
| 181:54 | peak of the wave. Yeah. Let's go back here. So for |
|
| 182:02 | , at this time, at this we have all these arrivals, |
|
| 182:10 | 1, 2, 3, 4 . And then uh this arrival also |
|
| 182:16 | arriving at this time. And so what makes um and they all have |
|
| 182:23 | own way blitz and their own but we don't know that when we |
|
| 182:27 | look at the size and again they each other and uh causes interpretation, |
|
| 182:33 | confusion. The amplitudes, these amplitudes are not shown on the previous |
|
| 182:40 | only the arrival times are shown. do carry useful information, but the |
|
| 182:45 | shows no indication at all. So , because of all these arriving, |
|
| 182:59 | arriving signals, different pathways, different share waves, P waves, |
|
| 183:04 | everything, reflections or refraction, everything in there. So some of it |
|
| 183:11 | gonna regard as signal and some of is noise. So let me ask |
|
| 183:19 | your tie uh what's the difference between moments. Yeah, yeah, that's |
|
| 183:35 | pretty close to what I'm looking for uh noise is actually signal that we |
|
| 183:44 | care about. That's what you But uh if we think about |
|
| 183:49 | maybe it's uh it's actually a signal we don't understand. So maybe if |
|
| 183:57 | think about this noise and uh more will learn something about the earth that |
|
| 184:04 | ignored first. We don't care about , but it really is signal that |
|
| 184:10 | we should be thinking about, but got to be smarter to understand it |
|
| 184:16 | because of that. The distinction between and noise is very subjective. And |
|
| 184:23 | if you think that this part of data is noise. I might think |
|
| 184:29 | the signal and vice first. back to you Stephanie. Um |
|
| 184:40 | is this statement? How do we compute complete this statement? Uh Beginning |
|
| 184:48 | the statement says that primary reflections from reflectors in the sub service have move |
|
| 184:53 | , which varies often often in which these ways literally literally hyperbolically or |
|
| 185:00 | So uh we'll talk your way through . Okay, we eliminate A. |
|
| 185:10 | B. Well, let's go back look at the cartoon. Okay, |
|
| 185:25 | here here is a reflection right Yeah. The unit. So it |
|
| 185:31 | to me like the earliest arrival as is at uh zero offset Back here |
|
| 185:38 | D zero Offset. Yeah, I to play with sinister rival the roster |
|
| 185:51 | if it's dipping. But here it it's not dipping. So this happens |
|
| 185:56 | dipping reflectors. But your answer is now multiple reflections. Uh and flatline |
|
| 186:05 | how we're gonna yeah, it's gonna the same. And in fact, |
|
| 186:14 | we go back here to the you know, uh this is uh |
|
| 186:20 | a multiple. It says it's a right here age. So that one |
|
| 186:25 | like a hyperbole to and it looks sort of a deep reflector. It |
|
| 186:30 | a lot like this except that you the, can you see this slope |
|
| 186:34 | here is less, this slope here more so this velocity is uh |
|
| 186:43 | This slope is flatter, This philosophy smaller than than it is. |
|
| 186:47 | so what we have is a hyperbolic with a slow velocity arriving late. |
|
| 186:55 | the reason it's arriving late is because spent its time echoing around in the |
|
| 186:59 | parts of the media. So that it. And then it also has |
|
| 187:03 | slow velocity, because as it's going and forth in the upper part of |
|
| 187:09 | media of the medium, those philosophies slow. So this is gonna be |
|
| 187:15 | . Uh but it's it's gonna be hyperbolic and furthermore, it's gonna be |
|
| 187:21 | other high purples in the cartoon. doesn't make any problems. But let's |
|
| 187:26 | down here for uh that one doesn't any. You can guarantee you can |
|
| 187:33 | sure that in the real world uh like that are gonna be lying right |
|
| 187:39 | top of your uh of your You're gonna be interested in a primary |
|
| 187:46 | that looks like this starts here and down here and crosses here somewhere at |
|
| 187:52 | offset. So uh you can be that there will be multiples interfering with |
|
| 187:59 | primary uh reflection of greatest interest. a simple application of Murphy's law. |
|
| 188:09 | gonna be a multiple that bothers Okay, next, uh has moved |
|
| 188:20 | . Which varies how about this? , very literally. And extrapolating back |
|
| 188:27 | the surface. And furthermore, it's to have an extended wave. So |
|
| 188:38 | let's look at here, uh ground is uh call that j that's |
|
| 188:43 | so j So it looks like it's causing much of a problem here. |
|
| 188:49 | uh the wavelet of this means that the peak of the of the ground |
|
| 188:55 | gonna be arriving here. But it's have to be a wave that expands |
|
| 189:00 | all these other times. So it's interfere with everything. And furthermore it's |
|
| 189:05 | have high amplitude. Why does it high active? Well, it's because |
|
| 189:12 | my my definition is a surface So the uh the empathy was contrary |
|
| 189:19 | the surface. Well, guess That's where we have our receivers. |
|
| 189:24 | the amplitude is gonna be on our is gonna be mostly most of the |
|
| 189:29 | is gonna be uh groundwater or surface which we don't want because it's only |
|
| 189:38 | to tell us about the shallow We want to know about the deeper |
|
| 189:42 | . We we want to um uh at reflections. So we're gonna have |
|
| 189:47 | do some clever data processing to see reflections underneath the ground wall. And |
|
| 189:56 | so we have another course in this this sequence. I will give you |
|
| 190:02 | few simple ideas, will get much thorough discussion of solving that problem. |
|
| 190:10 | I think it's Professor joe, is correct given that. Okay, so |
|
| 190:19 | is a fun topic. And so have 15 minutes to discuss. |
|
| 190:28 | so consider this uh seismic survey with places identified here A. And |
|
| 190:36 | Vector source in A. And is a vector source at B. |
|
| 190:42 | Um In both places there are citizen is receiver at a source from |
|
| 190:52 | . Along this vector. And this a receiver at be sourced from a |
|
| 190:59 | . Now the reciprocity theorem, a deep theorem of elasticity uh discovered over |
|
| 191:09 | years ago as applied in the seismic . That says that uh this relationship |
|
| 191:17 | true. So you take the force a. You make a dot |
|
| 191:22 | It's a vector. It force it . Make a dot product with vector |
|
| 191:27 | the data at a source from That dot product is the same as |
|
| 191:33 | corresponding dot product over here. So and the proof in the book by |
|
| 191:46 | , which is almost 100 years Yeah. Huh. For looking only |
|
| 191:54 | P waves, those dot products go because the forces in the same direction |
|
| 192:01 | uh as the data. So we're set the force is equal. And |
|
| 192:08 | what this says in this special case that it says the data measured at |
|
| 192:15 | source from B is actually exactly equal the data measured it be source and |
|
| 192:24 | . So that's called. Uh So that means is if you interchange the |
|
| 192:28 | and receiver position. The data is center. Okay, so before we |
|
| 192:38 | this, we should have known But all along in the bad old |
|
| 192:43 | we used to do split spread surveys so we would have sources and receivers |
|
| 192:48 | all spread all along here in two . And we would sort the data |
|
| 192:53 | that we could get a common midpoint gather and it would be illuminated from |
|
| 193:02 | both directions. So this one which arriving at this receiver would have started |
|
| 193:07 | here, coming down here and up and then uh source from both |
|
| 193:14 | We call it a split spread survey and received on both sides of the |
|
| 193:21 | . Now what we learned from the theorem is that we can obtain the |
|
| 193:25 | information using off end shooting. So only shoot to the left of the |
|
| 193:30 | the midpoint and all the receivers are the right of the midpoint, half |
|
| 193:39 | effort. And so when we realize suddenly we realize that we can do |
|
| 193:48 | streamer acquisition. And so of course off end shooting because the source is |
|
| 193:53 | here, the receivers are always down . And uh so we uh have |
|
| 194:03 | Only raised propagating like this in a environment. So in the early days |
|
| 194:09 | had only single streamers with less than ft long, you know five or |
|
| 194:16 | or 7000 ft long and with hydrophones intervals of about 100 ft. That |
|
| 194:22 | the kind of data that my father acquiring late in his career. And |
|
| 194:30 | reason we can get away with this because uh uh reciprocity theorem says we |
|
| 194:38 | need to have a source back here the same receivers from both from both |
|
| 194:46 | . And so uh now the reciprocity was about uh displacement, but you |
|
| 194:53 | easily extend that to put pressure. . Oh this is really useful for |
|
| 195:06 | when we analyze computers because uh the algorithms have computing costs which depend upon |
|
| 195:16 | number of source position. But in acquisition designs have many more sources than |
|
| 195:27 | . Uh Same old some acquisition designs many more sources than receivers. So |
|
| 195:35 | we interchange the roles of sources and in the computer, these algorithms are |
|
| 195:40 | efficient. Remember that these conclusions only to uh the waves for share waves |
|
| 195:51 | converted ways. We need the full rest process there. The version I |
|
| 195:56 | showed you um any of this Now I know what you're thinking, |
|
| 196:03 | thinking this looks pretty obvious. Let show you a thought experiment there uh |
|
| 196:12 | become very president for you. so imagine a two d problem in |
|
| 196:18 | plane here. And we have a here which elliptical in form and an |
|
| 196:25 | has two special places in it which called the far side and one is |
|
| 196:31 | and one is here. And I'll you about the properties of those two |
|
| 196:35 | in a second. For now let's that we have a source at one |
|
| 196:41 | and a receiver at the other Now here are the here's the special |
|
| 196:47 | of these two foes. It says uh if you if you run the |
|
| 196:53 | between this focus to any point on line and back to the other |
|
| 197:00 | it's the same length of string. matter where this point is including uh |
|
| 197:06 | like here, why this string from source to why to receive is the |
|
| 197:11 | length of string from uh X. a special property of the ellipse. |
|
| 197:19 | furthermore, these angles are the So these lines are like rays of |
|
| 197:26 | . Right? So that means that you fire a source, fire an |
|
| 197:34 | source here, all the rays from from all in points inside this reflector |
|
| 197:41 | end up at the receiver at exactly same time. So imagine an impulsive |
|
| 197:46 | and you get an impulsive reception with everywhere inside the uh the ellipse. |
|
| 197:57 | , those are that's what happens when have sources and receivers at the focus |
|
| 198:03 | of the ellipse. Now let's interchange and resumes. Now the sources here |
|
| 198:08 | the receiver is here and it's very you're going to get exactly the same |
|
| 198:13 | because of symmetry. Okay, that's surprising. Hold on to your |
|
| 198:18 | Now we're going to put uh source on the left and we're gonna remove |
|
| 198:25 | nose of this ellipse so that when source fires half the energy gets lost |
|
| 198:31 | space and the other half collects here at one instant at the receiver now |
|
| 198:37 | onto your teeth because now what the theorem says is that when you enter |
|
| 198:45 | in this situation in charge source and . So now the sources here, |
|
| 198:49 | receiver is here Because this is such narrow opening here are only like 5% |
|
| 198:57 | the energy gets lost to outer 95% of the energy is still inside |
|
| 199:04 | reflector and it all collects here. the reciprocity says that the data is |
|
| 199:13 | exactly exactly the same as in the case where half the energy got |
|
| 199:20 | So this is very counterintuitive, very . So when this was published by |
|
| 199:35 | smart uh um geophysicist at Texaco named , he's deceased now. But uh |
|
| 199:46 | posed this paradox in the pages of Journal. And we had a uh |
|
| 199:57 | discussion in the journal with famous uses coming down on both sides of the |
|
| 200:05 | . Is this the same data as other side? The other case or |
|
| 200:10 | ? And so the issue was finally by Professor Clara Clara Bell and his |
|
| 200:20 | Dillinger who eventually became my colleague at . And they did a computer |
|
| 200:28 | And here here here you can see ellipse with the nose off and here |
|
| 200:32 | can see the sources on the uh can see the sources on the left |
|
| 200:39 | uh most of the energy is staying the ellipse some of it gets past |
|
| 200:45 | and escape to outer space and here the energy and the resulting pressure um |
|
| 200:53 | that computerized experiment here now the interchange and receiver. And here we've got |
|
| 201:00 | source here, half the energy gets to outer space. And uh so |
|
| 201:05 | shows the energy uh arriving for every . And you see it's very different |
|
| 201:13 | this and here's the pressure arriving from angle. When you sum this |
|
| 201:27 | When when you sum this up, total uh total pressure coming from all |
|
| 201:34 | different res uh sums up to this .548 and it's the same sun for |
|
| 201:41 | , even though different contributions from the angles, it all sums up to |
|
| 201:46 | same. And um this gap you know, this is the part |
|
| 201:51 | got got lost. Whereas uh the is very different as you can see |
|
| 201:58 | your eyeball. So uh Claire bow now quite old, He's uh professor |
|
| 202:09 | at stanford and I think he's a about 90 still alive and kicking. |
|
| 202:16 | , very active. I understand it into the office of the day. |
|
| 202:25 | Stephanie, is this statement uh for ? Yeah, it's false because |
|
| 202:34 | the reciprocity theorem enables marine acquisition 1 boat marine acquisition. Uh Is |
|
| 202:44 | uh is this statement true. Is general statement of the reciprocity theorem. |
|
| 202:52 | like that. That true. that's good for you. Uh this |
|
| 202:59 | statement is a special case. In general case, it's false. Not |
|
| 203:05 | , but the special case we now the scale of reciprocity applies only to |
|
| 203:10 | waves and that one is true. by the way it's a very general |
|
| 203:14 | , it includes things like um and includes heterogeneity, it includes everything um |
|
| 203:23 | uh yes, so that's why it's powerful. It's only for p |
|
| 203:30 | So now in this lesson we've learned how the previous lessons on electricity led |
|
| 203:39 | the scalar wave equation for waves in ocean and for rock state leads to |
|
| 203:46 | vector wave equation, not real but for uniform as traffic rocks when |
|
| 203:57 | put in their source, then we how that equation gets modified and how |
|
| 204:04 | gets modified when there's layer in the . And then we looked briefly at |
|
| 204:10 | types of solutions, all of which gonna observe all those are in our |
|
| 204:16 | . And how the concept of elastic leads to significant operation and competition |
|
| 204:26 | So this is a good place uh to break for lunch Utah. This |
|
| 204:31 | a good place to cut the To to what your question is your |
|
| 204:44 | is about what or the ellipse. , so are we still recording? |
|
| 204:52 | , so this is good. keep it recorded. So and so |
|
| 204:55 | me your question. That's correct. go back here. Okay, share |
|
| 205:24 | pressure is proportional to the amplitude and energy is proportional to the square of |
|
| 205:29 | amplitude. Okay, so uh so one and what you measure is the |
|
| 205:34 | of all these angular contributions, The the the angle of arrival of |
|
| 205:39 | the ways. And so um this so what's the same is the uh |
|
| 205:48 | area under this which is the sum all the contributions from all the |
|
| 205:55 | And you can see that the the under this. So the part that |
|
| 206:00 | lost out here is out here. that uh that part got lost and |
|
| 206:07 | part that gets lost here is only the middle. So it has the |
|
| 206:11 | all these tales all the way So uh the area underneath this curve |
|
| 206:18 | black is the same as the area . Uh even though the energy is |
|
| 206:23 | as much. And so remember that energy is the square. So you |
|
| 206:27 | this uh take this curve and square and adjust the scale. And you |
|
| 206:34 | this curve. Same here, take uh and square it and adjust the |
|
| 206:40 | . And you get this curve. so uh it's the uh huh pressure |
|
| 206:48 | equivalent the amplitude which is uh the in these two situations, not the |
|
| 206:59 | . Okay, so let's uh break . And uh we will reconvene at |
|
| 207:06 | PM. Talk about um or we're talk about the solutions. So why |
|
| 207:17 | wave solutions to these |
|